Geometry and Trigonometry Formulas
- Distance between two points (x1, y1, z1), (x2, y2, z2)d = √(x1 − x2)2 + (y1 − y2)2 + (z1 − z2)2
- Coordinates of midpoint of a line with endpoints (x1, y1, z1), (x2, y2, z2)( x1 + x2 2 , y1 + y2 2 , z1 + z2 2 )
- Volume: Right pyramidV = 1 3 Ah, A = base area, h = height
- Volume: Right coneV = 1 3 πr2h, r = radius, h = height
- Area: Cone curveA = πrl, r = radius, l = slant height
- Volume: SphereV = 4 3 πr3, r = radius
- Surface area: SphereA = 4πr2, r = radius
- Sine rulea sinA = b sinB = c sinC
- Cosine rulec2 = a2 + b2 − 2ab cosC
cosC = a2 + b2 − c2 2ab - Area: TriangleA = 1 2 ab sinC
- Length of an arcl = rθ, r = radius, θ = angle in radians
- Area of a sectorA = 1 2 r2θ, r = radius, θ = angle in radians
- Identify for tan θtanθ = sinθ cosθ
- Pythagorean identitycos2θ + sin2θ = 1
- Double angle identitiessin2θ = 2 sinθ cosθ
cos2θ = cos2θ − sin2θ
= 2 cos2θ − 1
= 1 − 2 sin2θ

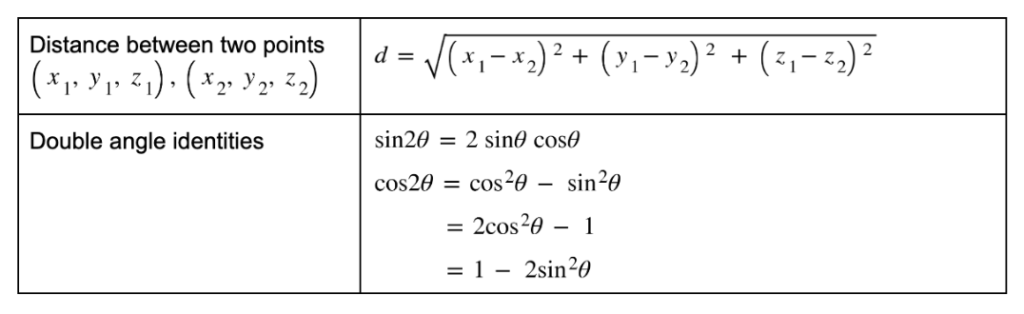
Geometry vs. Trigonometry: FAQs
Learn about the relationship and differences between these branches of mathematics.
Geometry is the study of shapes, sizes, properties of space, and relationships between points, lines, angles, and surfaces. It deals with figures in terms of their form, size, and position (e.g., calculating the area of a square, the volume of a sphere, or proving properties of triangles).
Trigonometry, on the other hand, is specifically the study of the relationships between the sides and angles of triangles. It primarily focuses on right triangles and uses trigonometric functions (like sine, cosine, and tangent) to calculate unknown side lengths or angles. While it uses geometric shapes (triangles), its focus is on the *measurements* derived from angle-side relationships.
No, they are not the same, but they are closely related branches of mathematics. Geometry is a broader field dealing with space and shapes in general, while trigonometry is a specialized area *within* geometry that focuses on triangles and the relationships between their sides and angles using specific ratios (trigonometric functions). Trigonometry uses geometric concepts to make calculations.
Trigonometry is fundamentally built upon geometric principles, particularly those related to triangles (especially right triangles). It uses the concepts of angles, lines, and lengths from geometry and adds the specific tools (trigonometric functions) to quantify the relationships between angles and side lengths. You need a foundation in geometry to understand why trigonometric identities and formulas work. Trigonometry provides tools to solve many geometric problems involving angles and lengths in triangles that might be difficult with pure geometry alone.




