Solving a system of two linear equations should be familiar to most of you. There are several methods of solving it, including substitution and subtraction of equations from each other. However, sometimes there can be three equations with three unknowns or even two equations with three unknowns. It is important to identify when those equations have unique, infinite amount or no solutions at all. The easiest way to do it is to solve the simultaneous equations. It is possible to think of a system of linear equations geometrically, where the solution is at the intersection of lines or planes. Thus the intersection can be a point, a line or a plane. Here is how to identify the amount of solutions that the system of equations has:

Unique solution there is only one set of variables that satisfy all equations. Intersection is a point.

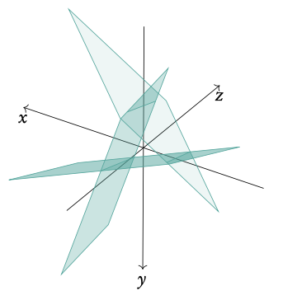
No solutions no set of variables satisfy all equations, usually you get 1 = 0 when solving the system. No intersection of all equations in one point.

Infinite amount of solutions infinite amount of variables satisfy the equation, meaning at least one free variable. Intersection in a line or plane.

Example: Solve the system of linear equations:

First rewrite (1.1) as y = 2 − 3x to substitute into (1.2):

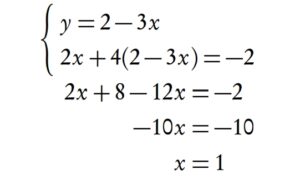
(1.1)3 + y = 2 ⇒ y = −1

The answer is: (1,−1). It can also be represented graphically, as an intersection of two lines in a single point.

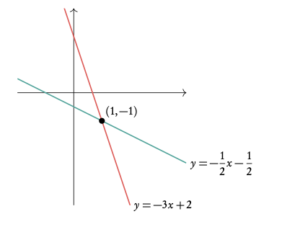
Example: Solve the system of linear equations:

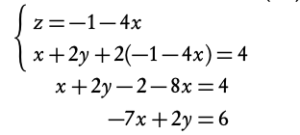
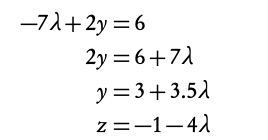
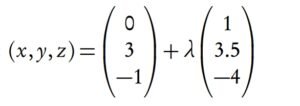
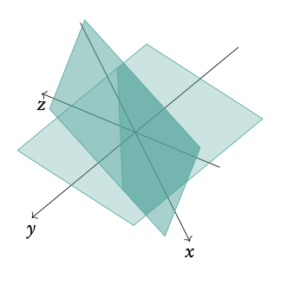
Rewrite equation (1.4) as z = −1 − 4x to substitute into (1.3):

There are not enough equations to find a unique solution, so we can do a substitution.

Let x =λ.

So our solution is:

Which means that there are infinite amount of solutions. Graphically it can be represented as two planes meeting in a line:

Example: Solve the system of linear equations:

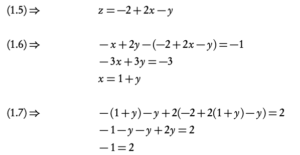
Which is not true, thus there are no solutions to this system of linear equations. It can be seen as three planes that do not intersect in the same point:

Linear Equations FAQs

A linear equation is an algebraic equation where each term is either a constant or the product of a constant and a single variable raised to the first power. This means variables do not have exponents other than 1, are not multiplied together, and do not appear in denominators, exponents, or roots.

When graphed on a coordinate plane, a linear equation with two variables (\(x\) and \(y\)) always produces a **straight line**. Examples include \(y = 2x + 1\), \(3x - 5y = 10\), or simply \(x = 4\).

Look for these characteristics to identify a linear equation:

Variables are only raised to the power of 1.
Variables are not multiplied together (e.g., no \(xy\) term).
Variables do not appear in the denominator of fractions.
Variables are not inside square roots or other radicals.
Variables are not in exponents.

Example Linear: \(2x + 3y = 5\), \(y = -x + 7\), \(z = 10\).
Example Non-Linear: \(x^2 + y = 4\) (x is squared), \(xy = 6\) (variables multiplied), \(y = \sqrt{x}\) (variable in root), \(y = 2^x\) (variable in exponent).

The goal is usually to isolate the variable. For a single-variable linear equation (like \(2x + 5 = 11\)):

Simplify both sides of the equation (combine like terms, distribute).
Use inverse operations to move terms:
- Add or subtract constants to get them away from the variable term.
- Multiply or divide to get the coefficient away from the variable.
Whatever you do to one side, do to the other to maintain balance.

Example: Solve \(2x + 5 = 11\)
Subtract 5 from both sides: 2x = 6
Divide both sides by 2: x = 3

A system of linear equations is a set of two or more linear equations that share the same variables. The "solution" to a system is a set of values for the variables that satisfies *all* equations in the system simultaneously.

Methods to solve systems include graphing (finding the intersection point), substitution, and elimination.

Since a linear equation with two variables (\(x, y\)) graphs as a straight line, you only need two points to draw it. Common methods:

Using two points: Choose two different values for \(x\), calculate the corresponding \(y\) values using the equation, plot the two points \((x, y)\), and draw a straight line through them. The x- and y-intercepts are often easy points to find (set \(y=0\) to find the x-intercept, set \(x=0\) to find the y-intercept).
Using Slope-Intercept Form (\(y = mx + b\)): Plot the y-intercept \((0, b)\). Then use the slope \(m\) (which is "rise over run") to find a second point. For example, if \(m = 2/3\), from the y-intercept, move up 2 units and right 3 units to find another point.

You can find the equation of a line using different information:

Given the slope (\(m\)) and y-intercept (\(b\)): Use the slope-intercept form \(y = mx + b\).
Given the slope (\(m\)) and a point \((x_1, y_1)\): Use the point-slope form \(y - y_1 = m(x - x_1)\). You can then rearrange this into slope-intercept or standard form.
Given two points \((x_1, y_1)\) and \((x_2, y_2)\): First, calculate the slope \(m = \frac{y_2 - y_1}{x_2 - x_1}\). Then, use the point-slope form with either of the two points and the calculated slope.

The **standard form** of a linear equation is \(Ax + By = C\), where \(A, B, C\) are integers, and \(A\) is usually non-negative.

Finding the equation of a tangent line to a curve at a specific point requires calculus (differentiation). A tangent line is a linear equation that touches the curve at that single point and has the same slope as the curve at that point.

Find the slope of the tangent line: Calculate the derivative of the function, \(f'(x)\). Evaluate the derivative at the x-coordinate of the given point to find the slope \(m\) at that point.
Find the y-coordinate of the point: If only the x-coordinate is given, plug it into the original function \(f(x)\) to find the y-coordinate \((y_1)\).
Use the point-slope form: With the slope \(m\) and the point \((x_1, y_1)\), write the equation of the tangent line as \(y - y_1 = m(x - x_1)\).

This linear equation represents the tangent line.

A function is linear if its graph is a straight line and its equation can be written in the form \(f(x) = mx + b\), where \(m\) is the slope and \(b\) is the y-intercept. This is equivalent to a linear equation in two variables \(y = mx + b\).

Equations where \(y\) is expressed as a linear combination of the input variable(s) to the first power are linear functions. Examples: \(f(x) = 3x - 2\), \(g(t) = 5t\), \(h(u) = 1/2 u + 0\). Non-examples: \(f(x) = x^2\), \(g(t) = \sqrt{t}\), \(h(u) = 1/u\).

The slope of a linear equation with two variables \(y\) and \(x\) measures the steepness of the line and the rate of change of \(y\) with respect to \(x\). It's represented by \(m\) in the slope-intercept form \(y = mx + b\).

You can find the slope:

From \(y = mx + b\) form: It's the coefficient of \(x\).
From two points \((x_1, y_1)\) and \((x_2, y_2)\): Calculate \(m = \frac{\text{Change in y}}{\text{Change in x}} = \frac{y_2 - y_1}{x_2 - x_1}\).
From standard form \(Ax + By = C\): If \(B \ne 0\), rearrange to solve for \(y\): \(By = -Ax + C\), so \(y = (-A/B)x + C/B\). The slope is \(-A/B\). If \(B=0\), the equation is \(Ax=C\) (a vertical line) and the slope is undefined.

Disclaimer: The information provided here is for general mathematical knowledge and educational purposes. Solving linear equations and systems, as well as graphing and finding line equations, are fundamental skills in algebra. Mastering these requires practice. For academic assistance, consult textbooks, online resources, or a math educator.