A complex number is defined as z = a + bi. Where a, b ∈ ℝ, a is the real part (ℜ) and b is the imaginary part (ℑ).

i = √−1

i² = −1

z = a + bi is the Cartesian form. z = r(cosθ+isinθ) is the polar form where r is the modulus and θ is the argument also sometimes stated as z = r cisθ.

Modulus r the absolute distance from the origin to the point.

Argument θ the angle between the x-axis and the line connecting the origin and the point.

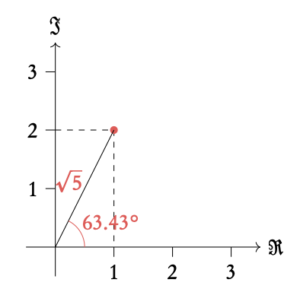
Instead of working in (x, y) coordinates, polar coordinates use the distance from the origin to the point (r, modulus) and the angle between the x-axis and the modulus (argument).

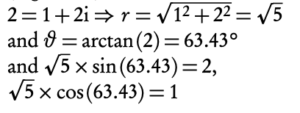
The conjugate of a complex number z̄ or z^∗, is defined as

z = a + bi ⇒ z̄ = a − bi

1.5.1 Complex numbers in the Cartesian form

Adding and subtracting complex numbers in Cartesian form is fairly straight forward. Add real and imaginary parts to each other:

(2+3i) + (4+9i) = 2 + 4 + 3i + 9i = 6+12i

Multiplying complex numbers is like multiplying two parentheses:

Division, however, is slightly more complex. Conjugates play a big role here, since a complex number multiplied by its conjugate is always equal to a real number.

Rewriting of a fraction with complex numbers

Convert the denominator into a real number by multiplying it with its conjugate.

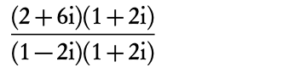
2. Expand the brackets and simplify, remember that i² = −1.

3. Write in a + bi form.

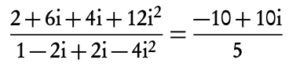
−2 + 2i

1.5.2 Complex numbers in the Polar form

Polar form allows us to do some operations quicker and more efficient, such as multiplication and division of complex numbers. The formulas can be shown for the following two complex numbers z₁ = r₁ cis(θ₁)and z₂ = r₂ cis(θ₂).

Note: cis x = cos x + i sin x .

Example:

Multiplication: z₁ × z₂ = r₁ × r₁ cis(θ₁ + θ₂)

Division:

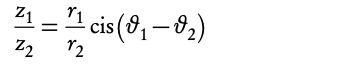
Euler’s and De Moivre’s theorem

These two theorems state the relationship between the trigonometric functions and the complex exponential function. This allows us to convert between Cartesian and Polar forms.

Euler’s Theorem

e^ix = cosx + isinx

De Moivre’s theorem

zⁿ = {r(cosx + isinx)}ⁿ =rⁿ {cos(nx) + isin(nx)}

De Moivre’s theorem can be derived from Euler’s through the exponential law for integer powers.

(e^ix)ⁿ = e^{ix n} = zⁿ

De Moivre’s theorem: proof by induction

Having seen the method of induction, we will now apply it to De Moivre’s theorem.

Example. Prove: zⁿ = (cos(x)isin(x))ⁿ = cos(nx) + isin(nx).

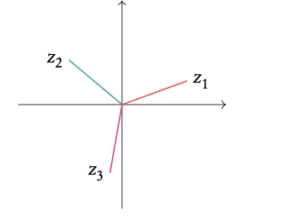
1.5.3 Nth roots of a complex number

n^th root of a complex number z is a number ω such that ωⁿ = z.

To find n^th root of a complex number (in polar form, z = r cis(θ)) you need to use the following formula:

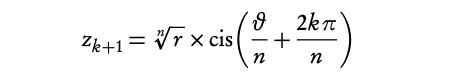
for k = 0, 1, 2, . . . , n − 1.

Finding complex roots

Find 3 roots of z³ = 4 + 4√3i and draw them on the complex plane.

Rewrite the complex number in polar form.

2. Insert values into formula.

3. Draw the roots on the complex plane, they should be equally spaced out with the same length.

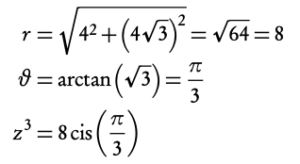
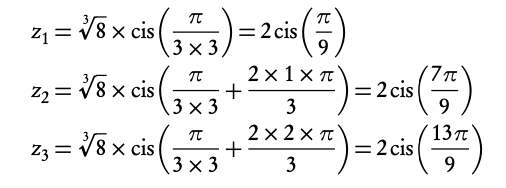
Complex Numbers FAQs

A complex number is a number that comprises a **real part** and an **imaginary part**. It is typically written in the form \(a + bi\), where:

\(a\) is the real part.
\(b\) is the real number representing the imaginary part's magnitude.
\(i\) is the imaginary unit, defined as the square root of -1 (so \(i^2 = -1\)).

Complex numbers extend the real number system, allowing us to solve equations (like \(x^2 + 1 = 0\)) that have no real solutions.

Yes. Every real number is a complex number with its imaginary part equal to zero. A real number \(a\) can be written in the complex form as \(a + 0i\).

This means the set of real numbers is a subset of the set of complex numbers.

The complex conjugate of a complex number \(z = a + bi\) is denoted as \(\bar{z}\) or \(z^*\), and it is obtained by changing the sign of the imaginary part. The conjugate of \(a + bi\) is \(a - bi\).

Example: The conjugate of \(3 + 4i\) is \(3 - 4i\). The conjugate of \(5i\) (which is \(0 + 5i\)) is \(-5i\) (\(0 - 5i\)). The conjugate of a real number \(7\) (which is \(7 + 0i\)) is \(7 - 0i = 7\).

Complex conjugates are important for division and finding moduli.

To find the conjugate of a complex number written in the form \(a + bi\), simply change the sign of the term with \(i\).

If the number is \(a + bi\), the conjugate is \(a - bi\).
If the number is \(a - bi\), the conjugate is \(a + bi\).
If the number is \(bi\) (purely imaginary), the conjugate is \(-bi\).
If the number is \(a\) (purely real), the conjugate is \(a\).

To divide complex numbers, you use the concept of the complex conjugate. If you want to calculate \(\frac{z_1}{z_2}\), where \(z_1 = a+bi\) and \(z_2 = c+di\), you multiply both the numerator and the denominator by the conjugate of the denominator (\(\bar{z_2}\)):

(a + bi) / (c + di) = [(a + bi) * (c - di)] / [(c + di) * (c - di)]

The denominator will always become a real number because \((c+di)(c-di) = c^2 - (di)^2 = c^2 - d^2 i^2 = c^2 - d^2(-1) = c^2 + d^2\). Then you expand the numerator and simplify to get the result in the standard \(A + Bi\) form.

The absolute value or modulus of a complex number \(z = a + bi\), denoted \(|z|\), is the distance from the origin \((0,0)\) to the point \((a, b)\) in the complex plane. It is calculated using the Pythagorean theorem:

|z| = |a + bi| = √(a² + b²)

Example: The modulus of \(3 + 4i\) is \(\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\). The modulus of \(-2i\) (which is \(0 - 2i\)) is \(\sqrt{0^2 + (-2)^2} = \sqrt{4} = 2\).

Complex numbers are graphed on a plane called the **complex plane** or **Argand plane**. This plane is similar to the Cartesian coordinate plane, but with specific axes:

The horizontal axis is the **real axis** (representing the real part \(a\)).
The vertical axis is the **imaginary axis** (representing the imaginary part \(b\), multiplied by \(i\)).

To plot the complex number \(z = a + bi\), you plot the point with coordinates \((a, b)\) on this plane. The real part \(a\) is the x-coordinate, and the coefficient of the imaginary part \(b\) is the y-coordinate.

Besides the standard (rectangular) form \(a + bi\), a complex number \(z\) can be represented in polar form \(r(\cos\theta + i\sin\theta)\) or \(re^{i\theta}\), where:

\(r\) is the **modulus** (distance from origin), \(r = |z| = \sqrt{a^2 + b^2}\).
\(\theta\) is the **argument** (angle from the positive real axis), typically found using \(\tan\theta = b/a\), but you must consider the quadrant of the point \((a,b)\) to get the correct angle.

The conversion involves calculating \(r\) and \(\theta\) from \(a\) and \(b\).

According to the **Fundamental Theorem of Algebra**, any polynomial equation of degree \(n\) (where \(n \ge 1\)) with complex coefficients has exactly \(n\) roots (solutions) in the complex number system, when counted with multiplicity.

For example, a quadratic equation (\(ax^2 + bx + c = 0\), degree 2) always has exactly 2 complex solutions (which might be real or repeated).

Disclaimer: The information provided here is for general mathematical knowledge and educational purposes. Complex numbers are a foundational topic in various fields of mathematics, physics, and engineering. For detailed study or specific problem-solving, consult textbooks, online resources, or a math educator.