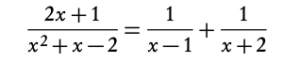Before you have learnt how to combine together different fractions to bring them under one denominator. However, sometimes you are required to do the opposite: split a fraction into distinct terms. In IB you will only be asked to split up fractions with two distinct linear terms in the denominator.
Solving partial fractions problems
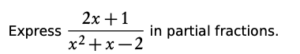
- Determine which linear terms make up the denominator
x2 + x − 2 = (x − 1)(x + 2)
2. Equate the fraction to sum of two fractions with unknown constants as numerators and the linear terms as denominators
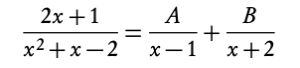
3. Multiply by the linear terms on both sides and determine the constant terms
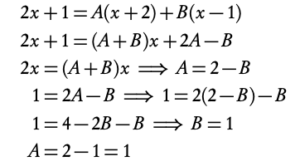
4. Plug in constant terms into the original equation