Fundamental theorem of algebra - Top Study Guide

The fundamental theorem of algebra any polynomial of degree n has n roots.

A degree of a polynomial is the largest exponent.

Example: If f(x) = 4x³ + 3x² + 7x + 9 then it is a polynomial at degree 3, and according to the fundamental theorem of algebra, will have 3 roots.

Any polynomial can be rewritten/factorized to include the roots:

a(x − r₁)(x − r₂)(x − r₃)···

where r₁, r₂, r₃, …, are all roots.

Note: some polynomials will have “double” or “triple” roots. Some may also have complex roots. Therefore a polynomial of degree 4 can have 4 real roots (of which 2, 3 or 4 could be the same) or 4 complex roots (of which 2, 3 or 4 could be the same) or 2 real and 2 complex roots.

Below are several examples of such situations.

Example: Complex roots of quadratic equations always come in conjugate pairs.

For example: 2x² − 3x + 4 has complex roots, i.e. (b² − 4ac) < 0. The roots are

x = \frac{3}{4} + \frac{i \sqrt{7}}{4} a n d x = \frac{3}{4} - \frac{i \sqrt{7}}{4}

can be shown graphically.

Example: f(x) = x² is a polynomial of degree 2, so it has 2 roots. However, the only root is x = 0. It means that x = 0 is a double root, meaning that the graph has a local minimum (or maximum) at that point.

Thus sometimes the polynomial can have a factor of (x − r_c)^d where r_c is a root and d is a number of occurrences of that root.

Example: Rewrite f(x) in a factorised form with real coefficients, where f(x) = x⁵ + x⁴ − 8x³ + ax² + bx + 24 with real coefficients a and b. It is also known that f(x) has a root x = −1 + i and one local minimum at x > 0.

First, it is important to remember that all roots come in conjugate pairs, meaning that f(x) also has a root x = −1 − i. From there it is possible to figure out that:

x + 1 = ±i

(x + 1)² = −1

x² + 2x + 2 = 0

Which is one of the factors of f(x). There are two ways to proceed, first one involves polynomial division, another involves sum and product of roots.

1. Since we know one factor of f (x), we can perform polynomial division to find other roots.

Since we know that we divided by one factor of the function, the remainder has to be equal to zero. Thus:

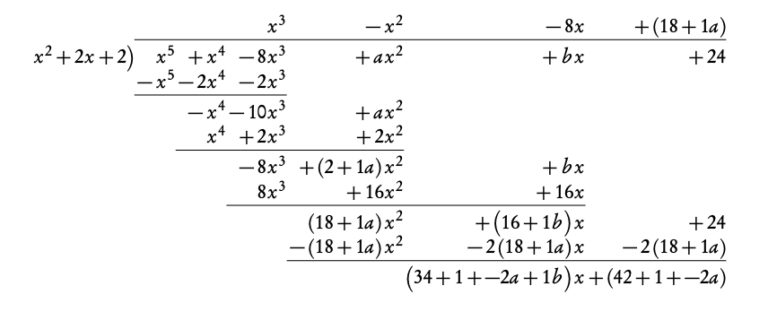
−2a − 12 = 0

a = −6

b + 16 − 2a − 36 = 0

b + 16 + 12 − 36 = 0

b = 8

Now we know values for a and b, so we can use them in what is left of our polynomial:

x³ − x² − 8x + (a + 18) = x³ − x² − 8x + 12

So we just need to solve our cubic equation. One way is to try to plug in specific values. For cubic polynomial g(x) = ax³ + bx² + cx + d , one of the roots is usually some factor of ^d/_a , so that it would be a rational fraction. As an example, our possible roots here are: ±12, ±6, ±4, ±3, ±2, ±1. By trying different values, you can find that x = 2 is one of our roots. Then it is required to perform polynomial division once again to get:

(x³ − x² − 8x + 12)÷(x − 2) = x² + x − 6 = (x + 3)(x − 2)

As you can see, x = 2 is a double root, since it comes up again. Thus our full factorised f(x) looks like this:

f(x) = (x² + 2x + 2)(x − 2)²(x + 3)

2. Another method requires formulas for sum and product of roots. Since we know that we have a double root (because of the minimum), we can easily find both roots. Let’s assume that double root is α and the other root is β. Sum of roots:

−1 + i − 1 − i + β + α + α = −¹/₁

2α + β = 1

Product of roots:

(−1 + i)(−1 − i) × β × α × α = (−1)⁵ × ²⁴/₁

2 × β × α × α = −24

β × α² = −12

Now solve simultaneous equations:

Again, solve the cubic equation, to get α = 2 and thus β = 3. Now factorise to get the same answer:

f(x) = (x² + 2x + 2)(x − 2)²(x + 3)

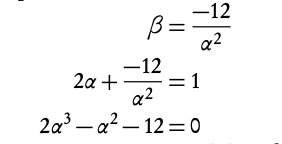
Frequently Asked Questions: The Fundamental Theorem of Algebra

What does the Fundamental Theorem of Algebra state?

The theorem states that every non-constant polynomial with complex coefficients has at least one complex root (or zero). A root is a value of the variable that makes the polynomial equal to zero.

A key consequence often stated is that a polynomial of degree n (where n ≥ 1) has exactly n complex roots, counting multiplicity.

What does "complex roots" mean?

Complex numbers include both real numbers and imaginary numbers. A complex number has the form a + bi, where a and b are real numbers, and i is the imaginary unit (where i² = -1).

So, the theorem guarantees that roots exist within the realm of complex numbers. They can be real numbers (where b=0) or non-real complex numbers (where b ≠ 0).

Why is the Fundamental Theorem of Algebra important?

It's fundamental because it guarantees the existence of roots for any polynomial. This is a powerful statement! Before this theorem, mathematicians weren't sure if roots always existed, especially for higher-degree polynomials. It ensures that a polynomial equation of degree n can always be "solved" (finding its roots) within the complex number system.

It's also crucial because it tells us *how many* roots to expect (exactly the degree of the polynomial, when counting multiplicity).

How do you "use" or "apply" the Fundamental Theorem of Algebra?

The theorem itself doesn't give you a method for *finding* the roots (except in very simple cases). Instead, it tells you what to expect:

Existence: You know a root exists for any non-constant polynomial.
Number of Roots: You know a polynomial of degree n has exactly n roots (counting multiplicity). This helps you know when you've found all of them. For example, a cubic polynomial (degree 3) will always have exactly 3 complex roots (which could be real, or a combination of real and non-real complex).
Factoring: Combined with the Factor Theorem, if c is a root of polynomial P(x), then (x - c) is a factor. The Fundamental Theorem ensures that any polynomial can theoretically be factored into linear factors over the complex numbers.

So, you "use" it by understanding its implications when trying to find roots using other methods (like factoring, the quadratic formula, rational root theorem, synthetic division, numerical methods).

Who proved the Fundamental Theorem of Algebra?

Several mathematicians attempted to prove the theorem over centuries. Jean-le-Rond d'Alembert made an important attempt, but his proof had gaps. Carl Friedrich Gauss provided the first generally accepted rigorous proof in his doctoral dissertation in 1799. He later provided several other proofs as well.

How do you find imaginary or complex roots using this theorem?

The theorem guarantees that these roots exist, but it doesn't provide a direct calculation method. To find non-real complex roots, you typically use other techniques:

Factoring: If you can factor out real roots using methods like the Rational Root Theorem and synthetic division, you're left with a lower-degree polynomial. If the remaining polynomial is quadratic (degree 2), you can use the quadratic formula, which will give complex roots if the discriminant (b²-4ac) is negative.
Recognizing Patterns: Some complex roots appear in conjugate pairs. If a + bi is a root of a polynomial with *real* coefficients, then a - bi must also be a root.

The theorem assures you that if your polynomial has degree n, you'll find exactly n roots in the complex numbers, even if some are non-real or repeated.