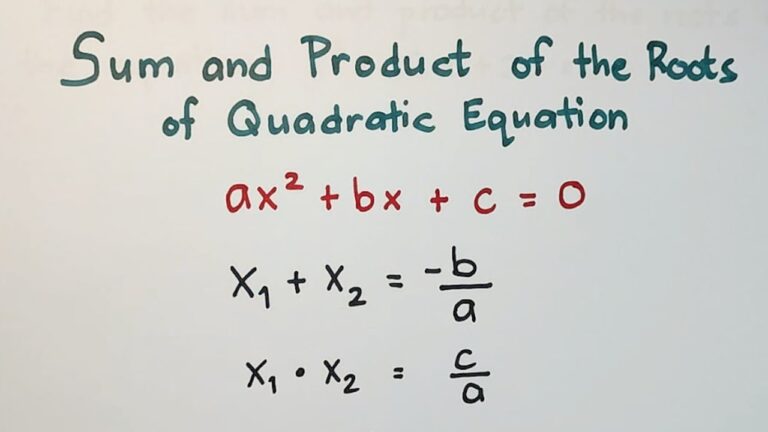Sums and products of roots

For any polynomial of form a_nxⁿ + a_n−1xⁿ⁻¹ + ··· + a₂x² + a₁x + a₀ = 0:

Sum of roots

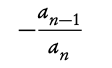
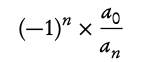
Product of roots:

Example: Given x² + 8x + k = 0, find both roots, when one is 3 times larger than another. Then find value of k.

First we need to find out what both roots are. Let x₁ = α, then x₂ = 3α. Using formula we get:

Sum of roots: − ⁸/₁

⇒ Thus: x₁ + x₂ = −8

α + 3α = −8

α = −2 = x₁

x₂ = 3 × −2 = −6

It means that we can factorise original polynomial as (x + 2)(x + 6) = 0, giving:

(x + 2)(x + 6) = x² + 8x + 12

Therefore, k = 12.

Understanding Roots of Quadratic Equations

What are the sum and product of roots of a quadratic equation? +

For a standard quadratic equation in the form \(ax^2 + bx + c = 0\), where \(a, b, c\) are coefficients and \(a \neq 0\), it has two roots (solutions), often denoted by the Greek letters alpha (\(\alpha\)) and beta (\(\beta\)).

The sum of the roots is \(\alpha + \beta\).
The product of the roots is \(\alpha \times \beta\).

These values have a direct relationship with the coefficients of the quadratic equation.

How do you find the sum and product of the roots using the coefficients? +

For a quadratic equation \(ax^2 + bx + c = 0\), where \(a \neq 0\), the sum and product of its roots (\(\alpha, \beta\)) can be found using simple formulas derived from Vieta's formulas:

Sum of roots (\(\alpha + \beta\)) = \(-\frac{b}{a}\)
Product of roots (\(\alpha \times \beta\)) = \(\frac{c}{a}\)

You just need to identify the coefficients \(a, b,\) and \(c\) from your equation and plug them into these formulas.

How do you find the quadratic equation if you know the sum and product of its roots? +

If you are given the sum (S) and the product (P) of the roots, you can construct a quadratic equation using the following general form:

\(x^2 - (\text{Sum of roots})x + (\text{Product of roots}) = 0\)

So, the equation is:

\(x^2 - Sx + P = 0\)

Note that this gives you *one* such equation. Any equation \(k(x^2 - Sx + P) = 0\), where \(k\) is any non-zero constant, will have the same roots and thus the same sum and product.