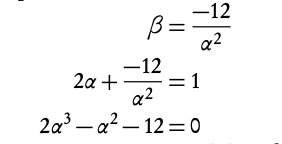Fundamental theorem of algebra

The fundamental theorem of algebra any polynomial of degree n has n roots.

A degree of a polynomial is the largest exponent.

Example: If f(x) = 4x³ + 3x² + 7x + 9 then it is a polynomial at degree 3, and according to the fundamental theorem of algebra, will have 3 roots.

Any polynomial can be rewritten/factorized to include the roots:

a(x − r₁)(x − r₂)(x − r₃)···

where r₁, r₂, r₃, …, are all roots.

Note: some polynomials will have “double” or “triple” roots. Some may also have complex roots. Therefore a polynomial of degree 4 can have 4 real roots (of which 2, 3 or 4 could be the same) or 4 complex roots (of which 2, 3 or 4 could be the same) or 2 real and 2 complex roots.

Below are several examples of such situations.

Example: Complex roots of quadratic equations always come in conjugate pairs.

For example: 2x² − 3x + 4 has complex roots, i.e. (b² − 4ac) < 0. The roots are

x = \frac{3}{4} + \frac{i \sqrt{7}}{4} a n d x = \frac{3}{4} - \frac{i \sqrt{7}}{4}

can be shown graphically.

Example: f(x) = x² is a polynomial of degree 2, so it has 2 roots. However, the only root is x = 0. It means that x = 0 is a double root, meaning that the graph has a local minimum (or maximum) at that point.

Thus sometimes the polynomial can have a factor of (x − r_c)^d where r_c is a root and d is a number of occurrences of that root.

Example: Rewrite f(x) in a factorised form with real coefficients, where f(x) = x⁵ + x⁴ − 8x³ + ax² + bx + 24 with real coefficients a and b. It is also known that f(x) has a root x = −1 + i and one local minimum at x > 0.

First, it is important to remember that all roots come in conjugate pairs, meaning that f(x) also has a root x = −1 − i. From there it is possible to figure out that:

x + 1 = ±i

(x + 1)² = −1

x² + 2x + 2 = 0

Which is one of the factors of f(x). There are two ways to proceed, first one involves polynomial division, another involves sum and product of roots.

1. Since we know one factor of f (x), we can perform polynomial division to find other roots.

Since we know that we divided by one factor of the function, the remainder has to be equal to zero. Thus:

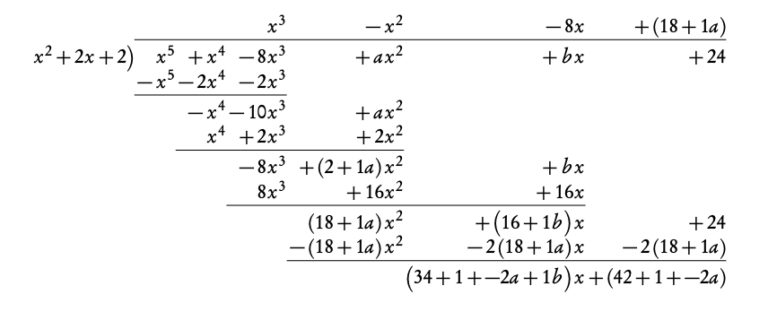
−2a − 12 = 0

a = −6

b + 16 − 2a − 36 = 0

b + 16 + 12 − 36 = 0

b = 8

Now we know values for a and b, so we can use them in what is left of our polynomial:

x³ − x² − 8x + (a + 18) = x³ − x² − 8x + 12

So we just need to solve our cubic equation. One way is to try to plug in specific values. For cubic polynomial g(x) = ax³ + bx² + cx + d , one of the roots is usually some factor of ^d/_a , so that it would be a rational fraction. As an example, our possible roots here are: ±12, ±6, ±4, ±3, ±2, ±1. By trying different values, you can find that x = 2 is one of our roots. Then it is required to perform polynomial division once again to get:

(x³ − x² − 8x + 12)÷(x − 2) = x² + x − 6 = (x + 3)(x − 2)

As you can see, x = 2 is a double root, since it comes up again. Thus our full factorised f(x) looks like this:

f(x) = (x² + 2x + 2)(x − 2)²(x + 3)

2. Another method requires formulas for sum and product of roots. Since we know that we have a double root (because of the minimum), we can easily find both roots. Let’s assume that double root is α and the other root is β. Sum of roots:

−1 + i − 1 − i + β + α + α = −¹/₁

2α + β = 1

Product of roots:

(−1 + i)(−1 − i) × β × α × α = (−1)⁵ × ²⁴/₁

2 × β × α × α = −24

β × α² = −12

Now solve simultaneous equations: