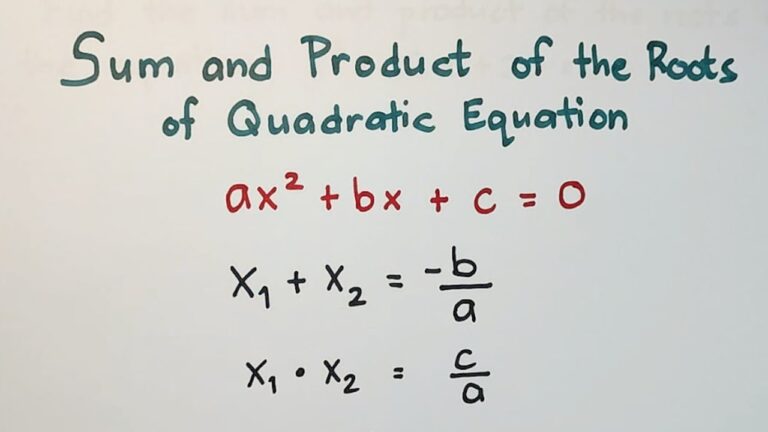For any polynomial of form anxn + an−1xn−1 + ··· + a2x2 + a1x + a0 = 0:
Sum of roots
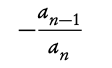
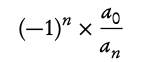
First we need to find out what both roots are. Let x1 = α, then x2 = 3α. Using formula we get:
Sum of roots: − 8/1
⇒ Thus: x1 + x2 = −8
α + 3α = −8
α = −2 = x1
x2 = 3 × −2 = −6
Sum and Product of Roots Calculator
Master Quadratic Equations with Interactive Tools
For a standard quadratic equation in the form \(ax^2 + bx + c = 0\), where \(a, b, c\) are coefficients and \(a \neq 0\), the equation has two roots (solutions), commonly denoted by Greek letters alpha (\(\alpha\)) and beta (\(\beta\)).
- The sum of the roots is \(\alpha + \beta\)
- The product of the roots is \(\alpha \times \beta\)
These values have a direct relationship with the coefficients of the quadratic equation, as described by Vieta's formulas.
For a quadratic equation \(ax^2 + bx + c = 0\) where \(a \neq 0\), Vieta's formulas give us:
- Sum of roots: \(\alpha + \beta = -\frac{b}{a}\)
- Product of roots: \(\alpha \times \beta = \frac{c}{a}\)
Example: For the equation \(2x^2 - 6x + 4 = 0\)
Here: \(a = 2\), \(b = -6\), \(c = 4\)
Sum of roots = \(-\frac{-6}{2} = 3\)
Product of roots = \(\frac{4}{2} = 2\)
Simply identify the coefficients and plug them into these formulas!
If you know the sum (S) and product (P) of the roots, you can construct a quadratic equation using:
Or: \(x^2 - Sx + P = 0\)
Example: If sum = 7 and product = 12
The equation is: \(x^2 - 7x + 12 = 0\)
This factors as: \((x - 3)(x - 4) = 0\)
Roots are: \(x = 3\) and \(x = 4\)
Verify: \(3 + 4 = 7\) ✓ and \(3 \times 4 = 12\) ✓
Note: Any equation \(k(x^2 - Sx + P) = 0\) where \(k \neq 0\) will have the same roots.
Vieta's formulas (named after French mathematician François Viète) establish the relationship between the roots of a polynomial and its coefficients.
For quadratic equations, these formulas are particularly useful because they allow you to:
- Find properties of roots without solving the equation
- Quickly check if your calculated roots are correct
- Construct equations when you know the roots
- Solve complex mathematical problems more efficiently
Vieta's formulas work even when the roots are complex numbers!
For example, if a quadratic equation has complex roots \(\alpha = p + qi\) and \(\beta = p - qi\) (complex conjugates):
- Sum: \((p + qi) + (p - qi) = 2p\) (a real number)
- Product: \((p + qi)(p - qi) = p^2 + q^2\) (a real number)
Example: For \(x^2 - 4x + 13 = 0\)
Sum = \(-\frac{-4}{1} = 4\)
Product = \(\frac{13}{1} = 13\)
Roots are: \(2 + 3i\) and \(2 - 3i\)
Verify: \((2+3i) + (2-3i) = 4\) ✓
Special Case 1: When \(a = 1\) (Monic quadratic)
For \(x^2 + bx + c = 0\):
- Sum of roots = \(-b\)
- Product of roots = \(c\)
Special Case 2: When \(b = 0\)
For \(ax^2 + c = 0\):
- Sum of roots = \(0\) (roots are negatives of each other)
- Product of roots = \(\frac{c}{a}\)
Special Case 3: When \(c = 0\)
For \(ax^2 + bx = 0\):
- Sum of roots = \(-\frac{b}{a}\)
- Product of roots = \(0\) (one root is zero)
🧮 Interactive Calculator Suite
Enter the coefficients of the quadratic equation \(ax^2 + bx + c = 0\):
Enter the sum and product of roots to form the equation:
Enter the two roots to verify sum and product: