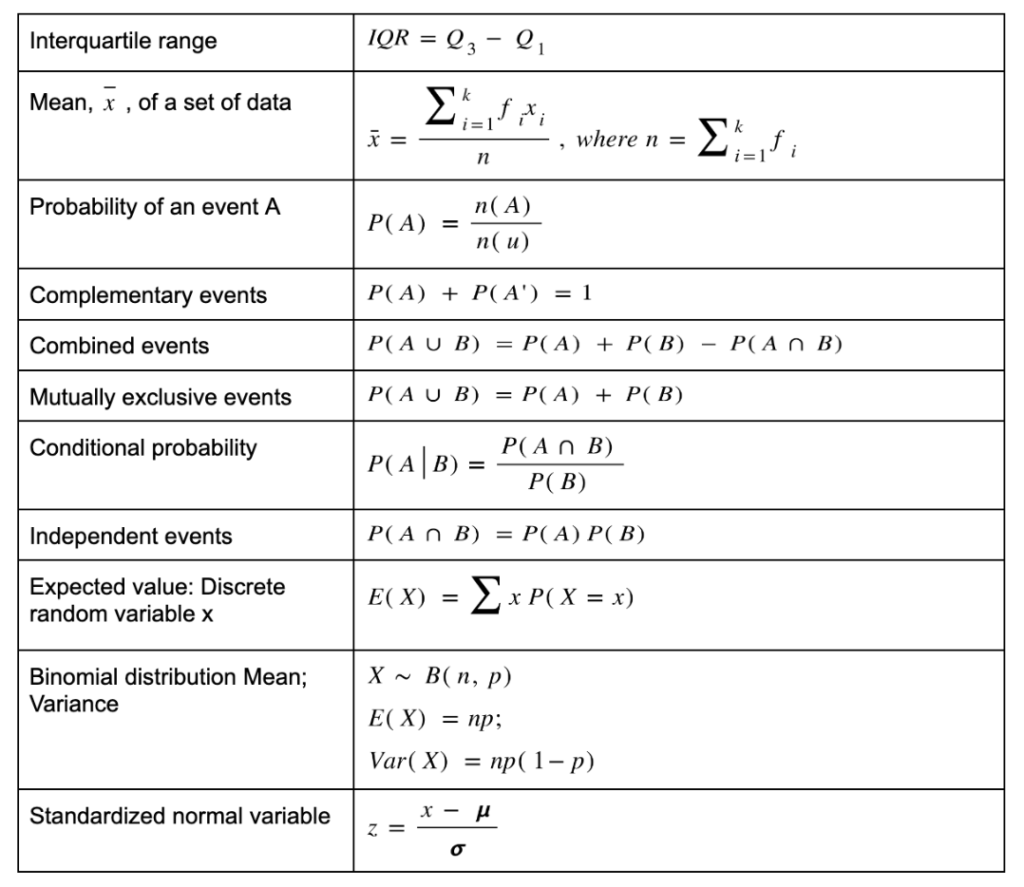
Statistics and Probability Formulae AA SL & AA HL

Statistics is the scientific discipline that involves the collection, organization, analysis, interpretation, and presentation of data. It's used to understand variability, make informed decisions, and draw conclusions about populations based on samples. It provides methods for summarizing data (descriptive statistics) and making inferences about larger groups (inferential statistics).

A statistical question is a question that can be answered by collecting data and where there will be variation in that data. It anticipates a variety of answers, rather than a single, fixed answer. For example, "How tall is the tallest building in the city?" is *not* a statistical question. "How tall are the buildings in the city?" *is* a statistical question because you expect the heights to vary.

"Algebra statistics" isn't a formal branch of mathematics, but rather refers to the extensive use of algebraic concepts and techniques within the field of statistics. Algebra is essential for understanding and manipulating statistical formulas, solving for unknown values in statistical models, working with equations for regression lines, and deriving statistical properties. You use algebra *to do* statistics.

A parameter is a numerical value that describes a characteristic of an entire population. For example, the average height of *all* adults in a country or the proportion of *all* voters who support a certain candidate are population parameters. Parameters are often unknown and estimated using statistics from a sample.

A statistic is a numerical value that describes a characteristic of a sample. It's calculated from the data collected from a subset of the population. For example, the average height of 100 randomly selected adults in a country or the proportion of 500 surveyed voters who support a candidate are sample statistics. Statistics are used to estimate population parameters.

So, a parameter describes the population, and a statistic describes the sample.

In statistics, 'n' almost always represents the sample size – the number of observations or individuals included in a dataset or sample. A capital 'N' is sometimes used to represent the size of the entire population, while lowercase 'n' is for the sample.

Variance is a measure of how spread out a set of data is from its mean (average). It's calculated as the average of the squared differences from the mean. A higher variance indicates that data points are more spread out from the mean; a lower variance indicates they are clustered closer to the mean.

The formula for sample variance (\(s^2\)) is: \(s^2 = \frac{\sum (x_i - \bar{x})^2}{n-1}\), where \(x_i\) are individual data points, \(\bar{x}\) is the sample mean, and \(n\) is the sample size.

Standard deviation (often denoted by 's' for sample standard deviation, or '\(\sigma\)' for population standard deviation) is the square root of the variance. It's the most common measure of data dispersion and is expressed in the same units as the data itself. It tells you, on average, how far each data point is from the mean.

Formula for sample standard deviation (s): \(s = \sqrt{s^2} = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n-1}}\).

The mean is the most common type of average. It's calculated by summing all the values in a dataset and dividing by the number of values. It's sensitive to extreme values (outliers).

Sample Mean (\(\bar{x}\)): \( \bar{x} = \frac{\sum x_i}{n} \)

The mode is the value that appears most frequently in a dataset. A dataset can have one mode (unimodal), multiple modes (multimodal), or no mode (if all values appear with the same frequency). It's useful for categorical or discrete data and is not affected by outliers.

To find the mode, count how many times each value appears and identify the value(s) with the highest count.

The range is the simplest measure of dispersion. It is the difference between the highest value and the lowest value in a dataset. It's easy to calculate but is highly sensitive to outliers.

Range = Maximum Value - Minimum Value

These are the three most common measures of central tendency, used to describe the "center" or typical value of a dataset:

• Mean: The arithmetic average (sum of values divided by count).
• Median: The middle value in a dataset that has been ordered from least to greatest. If there's an even number of values, it's the average of the two middle values. It's less affected by outliers than the mean.
• Mode: The value that appears most frequently.

Frequency in statistics refers to the number of times a particular value or category occurs in a dataset. A frequency distribution is a table or graph that shows how often each value or range of values appears.

To find frequency, you typically sort or group your data and then count the occurrences of each distinct value or within each defined interval (for continuous data).

Relative frequency is the proportion or percentage of times a specific value or category occurs in a dataset compared to the total number of observations. It's calculated by dividing the frequency of a value by the total number of data points.

Relative Frequency = (Frequency of a value) / (Total number of observations)

The sum of all relative frequencies in a dataset should equal 1 (or 100%).

Descriptive statistics are methods used to summarize, organize, and simplify data. They describe the basic features of the data. Examples include calculating measures of central tendency (mean, median, mode), measures of dispersion (variance, standard deviation, range), and creating charts and graphs (histograms, bar charts, box plots). Descriptive statistics help you understand what the data "looks like" but don't allow you to draw conclusions beyond the data at hand.

Inferential statistics are methods used to make inferences, predictions, and generalizations about a population based on data from a sample. Because it's often impossible to study an entire population, we use samples. Inferential statistics uses probability theory to determine how likely it is that the results from a sample can be applied to the larger population. Techniques include hypothesis testing, confidence intervals, and regression analysis.

Statistical significance indicates whether the results observed in a study (usually from a sample) are likely due to a real effect or simply due to random chance. When a result is statistically significant, it means that if the null hypothesis (the idea that there is no real effect or difference) were true, the probability of observing data as extreme as (or more extreme than) what was collected is very low. This low probability is quantified by the p-value.

The p-value (probability value) is the probability of obtaining test results at least as extreme as the results actually observed, assuming that the null hypothesis is true. A small p-value (typically ≤ 0.05, depending on the chosen significance level) suggests that the observed data is unlikely if the null hypothesis is true, leading you to reject the null hypothesis and conclude there is statistical significance. A large p-value suggests the data is consistent with the null hypothesis.

This phrase, famously the title of a book by Darrell Huff, refers to various ways statistics can be misused or presented deceptively to create a misleading impression. Techniques include:

• Biased sampling methods.
• Cherry-picking data or time periods.
• Using misleading graphs (e.g., truncated axes, manipulating proportions).
• Confusing correlation with causation.
• Using inappropriate averages (e.g., mean instead of median with outliers).
• Presenting percentages without the base numbers.

Understanding these techniques is important for critically evaluating statistical claims.

Difficulty is subjective. Many students find introductory statistics less abstract than calculus, as it deals more directly with data and real-world problems. However, it requires careful understanding of concepts, logical reasoning, and often involves word problems. AP Statistics is considered a challenging but manageable course, requiring strong reading comprehension and analytical skills. Success often depends more on conceptual understanding and problem-solving than on complex algebraic manipulation.

Probability is a branch of mathematics that quantifies the likelihood of an event occurring. It is a number between 0 and 1 (or 0% and 100%), where 0 means the event is impossible and 1 (or 100%) means the event is certain to happen. It deals with randomness and chance.

For simple events with equally likely outcomes (theoretical probability), the probability is calculated as:

P(Event) = (Number of favorable outcomes) / (Total number of possible outcomes)

For example, the probability of flipping heads on a fair coin is 1/2 (1 favorable outcome: heads; 2 possible outcomes: heads or tails).

Calculating probability for more complex scenarios involves using rules like the addition rule, multiplication rule, and understanding concepts like conditional probability and probability distributions.

Theoretical probability is based on reasoning about the possible outcomes of an event without actually performing the experiment. It assumes that all outcomes are equally likely. It answers questions like "What *should* happen in theory?". The formula is (Number of favorable outcomes) / (Total number of possible outcomes).

Experimental probability (also called empirical probability) is based on the results of actual experiments or observations. It's calculated after you have performed the experiment by dividing the number of times the event occurred by the total number of trials. It answers questions like "What *did* happen?".

P(Event) = (Number of times the event occurred) / (Total number of trials)

As the number of trials increases, experimental probability tends to get closer to the theoretical probability (Law of Large Numbers).

No. The probability of any event must be a value between 0 and 1, inclusive (0 ≤ P(Event) ≤ 1). A probability of 0 means the event is impossible, and a probability of 1 means the event is certain. Any value outside this range is not a valid probability.

Conditional probability is the probability of an event occurring *given that another event has already occurred*. It measures the likelihood of an event A happening, given that event B has already happened. It is denoted as P(A|B) and calculated as P(A|B) = P(A and B) / P(B), where P(A and B) is the probability that both events A and B occur, and P(B) is the probability of event B occurring (and P(B) > 0).

A probability distribution is a function or table that lists all the possible outcomes of a random variable and their corresponding probabilities. It completely describes the probability of any event occurring. There are different types of probability distributions depending on whether the variable is discrete (e.g., number of heads in coin flips) or continuous (e.g., height or weight).

• Discrete Probability Distributions: Use a Probability Mass Function (PMF).
• Continuous Probability Distributions: Use a Probability Density Function (PDF).

For a continuous random variable, a Probability Density Function (PDF) is a function whose value at any given point can be interpreted as a relative likelihood for the random variable to take on that value. Unlike discrete distributions, the value of the PDF at a specific point is *not* the probability of the variable equalling that point (which is typically zero for continuous variables). Instead, the probability that the variable falls within a specific range is given by the integral of the PDF over that range (the area under the curve).

For a discrete random variable, a Probability Mass Function (PMF) is a function that gives the probability that the variable takes on a specific value. It directly lists the probability for each possible outcome. The sum of all probabilities for all possible outcomes must equal 1.