IB

Statistics and Probability Formulae AA HL only

3 years ago
Last Update on February 13, 2026
8 mins
500 Views
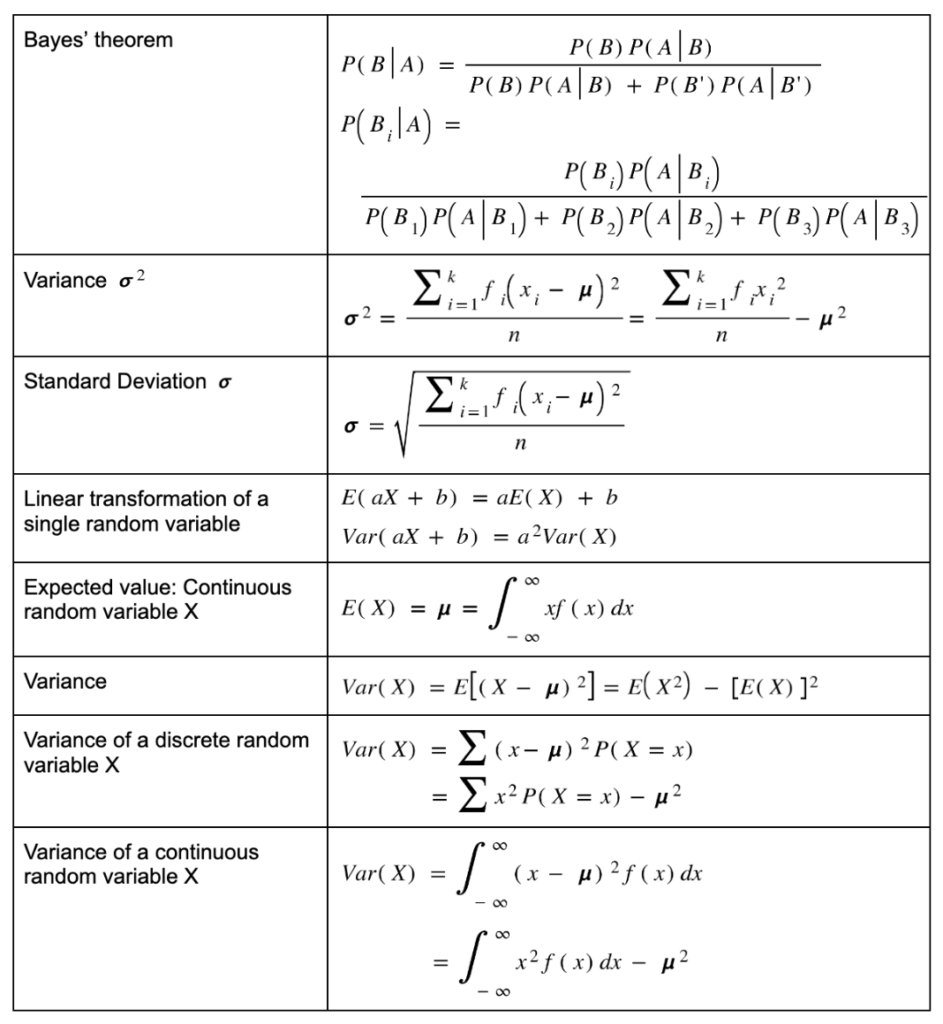
Master statistics and probability for IB Math AA HL with our comprehensive guide. Probability distributions, hypothesis testing, confidence intervals, Bayes' theorem & statistical inference. Interactive calculator included.
"Statistics and Probability Formulae AA HL banner with mathematical symbols and normal distribution curve on blue gradient background"
"Comprehensive guide to Statistics and Probability formulas for IB Mathematics AA Higher Level - Essential formulas, distributions, and problem-solving techniques"

Statistics and Probability Formulae AA HL: Complete Advanced Guide for IB Math Higher Level

Welcome to the definitive guide for Statistics and Probability Formulae in IB Mathematics Analysis and Approaches Higher Level—the most sophisticated statistics curriculum in secondary education. This comprehensive resource covers all advanced statistical concepts including probability theory, discrete and continuous distributions, expected value and variance, hypothesis testing, confidence intervals, chi-squared tests, correlation, regression, and Bayes' theorem. Mastery of these advanced statistical techniques is essential for achieving top marks in AA HL and provides the foundation for university-level statistics, data science, econometrics, and quantitative research in any field.

Understanding AA HL Statistics

IB Math AA HL statistics extends far beyond descriptive statistics and basic probability, encompassing rigorous probability theory, multiple probability distributions, statistical inference, hypothesis testing, and advanced modeling techniques. Unlike AA SL which focuses on understanding and applying standard statistical methods, AA HL demands theoretical understanding of probability distributions, mathematical derivations of formulas, ability to conduct formal hypothesis tests, and sophisticated interpretation of statistical results. These skills are indispensable for STEM degrees, economics, psychology, medicine, and any field requiring quantitative analysis of data and uncertainty.

Probability: Foundation Concepts

Conditional Probability

Conditional probability measures the probability of event A occurring given that event B has already occurred.

Conditional Probability Formula
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]

Read as: "Probability of A given B"

Valid when \( P(B) > 0 \)

Independent Events

Independence Condition
\[ P(A \cap B) = P(A) \times P(B) \]

Or equivalently: \( P(A|B) = P(A) \)

Events are independent when occurrence of one doesn't affect the other

Bayes' Theorem

Bayes' theorem reverses conditional probability, allowing calculation of P(B|A) from P(A|B).

Bayes' Theorem (Two Events)
\[ P(B|A) = \frac{P(B) \cdot P(A|B)}{P(B) \cdot P(A|B) + P(B') \cdot P(A|B')} \]

Where \( B' \) is the complement of B

Bayes' Theorem (Multiple Events)
\[ P(B_i|A) = \frac{P(B_i) \cdot P(A|B_i)}{\sum_{j=1}^{n} P(B_j) \cdot P(A|B_j)} \]

For mutually exclusive and exhaustive events \( B_1, B_2, \ldots, B_n \)

Example: Bayes' Theorem Application

A medical test is 95% accurate for detecting a disease (sensitivity) and 90% accurate for healthy patients (specificity). If 2% of the population has the disease, what's the probability someone has the disease given a positive test?

Solution:

Let D = has disease, T = positive test

\( P(D) = 0.02 \), \( P(D') = 0.98 \)

\( P(T|D) = 0.95 \), \( P(T|D') = 0.10 \)

\( P(D|T) = \frac{0.02 \times 0.95}{0.02 \times 0.95 + 0.98 \times 0.10} = \frac{0.019}{0.019 + 0.098} = \frac{0.019}{0.117} \approx 0.162 \)

Only 16.2% probability—highlighting the importance of base rates!

Discrete Random Variables

Expected Value

Expected Value of Discrete Random Variable
\[ E(X) = \mu = \sum_{i} x_i \cdot P(X = x_i) \]

Sum over all possible values \( x_i \)

Weighted average of outcomes by their probabilities

Variance and Standard Deviation

Variance of Discrete Random Variable
\[ \text{Var}(X) = \sigma^2 = \sum_{i} (x_i - \mu)^2 \cdot P(X = x_i) \]

Alternative formula (often easier):

\[ \text{Var}(X) = E(X^2) - [E(X)]^2 = \sum_{i} x_i^2 \cdot P(X = x_i) - \mu^2 \]
Standard Deviation
\[ \sigma = \sqrt{\text{Var}(X)} = \sqrt{\sum_{i} (x_i - \mu)^2 \cdot P(X = x_i)} \]

Binomial Distribution

Models number of successes in n independent trials with constant probability p.

Binomial Probability Formula
\[ P(X = r) = \binom{n}{r} p^r (1-p)^{n-r} \]

Where \( X \sim B(n, p) \)

\( n \) = number of trials, \( p \) = probability of success

Binomial Mean and Variance
\[ E(X) = np \] \[ \text{Var}(X) = np(1-p) = npq \]

Where \( q = 1 - p \)

Poisson Distribution

Models number of events occurring in a fixed interval when events occur independently at constant average rate.

Poisson Probability Formula
\[ P(X = r) = \frac{e^{-\lambda} \lambda^r}{r!} \]

Where \( X \sim \text{Po}(\lambda) \)

\( \lambda \) = mean number of events per interval

Poisson Mean and Variance
\[ E(X) = \lambda \] \[ \text{Var}(X) = \lambda \]

Unique property: mean equals variance

Poisson as Binomial Approximation

When \( n \) is large and \( p \) is small, \( B(n, p) \approx \text{Po}(np) \)

Rule of thumb: Use when \( n > 50 \) and \( np < 5 \)

Continuous Random Variables

Probability Density Function (PDF)

Properties of PDF
\[ f(x) \geq 0 \text{ for all } x \] \[ \int_{-\infty}^{\infty} f(x) \, dx = 1 \] \[ P(a \leq X \leq b) = \int_a^b f(x) \, dx \]

For continuous variables, \( P(X = a) = 0 \)

Expected Value and Variance (Continuous)

Expected Value of Continuous Random Variable
\[ E(X) = \mu = \int_{-\infty}^{\infty} x \cdot f(x) \, dx \]
Variance of Continuous Random Variable
\[ \text{Var}(X) = \int_{-\infty}^{\infty} (x - \mu)^2 \cdot f(x) \, dx \]

Alternative formula:

\[ \text{Var}(X) = E(X^2) - [E(X)]^2 = \int_{-\infty}^{\infty} x^2 \cdot f(x) \, dx - \mu^2 \]

Normal Distribution

The normal distribution is the most important continuous distribution in statistics.

Normal Distribution PDF
\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

Notation: \( X \sim N(\mu, \sigma^2) \)

Standardization (Z-Score)
\[ Z = \frac{X - \mu}{\sigma} \]

If \( X \sim N(\mu, \sigma^2) \), then \( Z \sim N(0, 1) \)

Use GDC or tables to find probabilities

Empirical Rule (68-95-99.7 Rule)
  • 68% of data within \( \mu \pm \sigma \)
  • 95% of data within \( \mu \pm 2\sigma \)
  • 99.7% of data within \( \mu \pm 3\sigma \)

Linear Transformations and Combinations

Linear Transformation of Single Variable

Linear Transformation Rules
\[ E(aX + b) = aE(X) + b \] \[ \text{Var}(aX + b) = a^2 \text{Var}(X) \]

Adding constant shifts mean but doesn't affect variance

Multiplying by constant scales both mean and variance

Linear Combinations of Random Variables

Sum/Difference of Random Variables
\[ E(X \pm Y) = E(X) \pm E(Y) \]

If X and Y are independent:

\[ \text{Var}(X \pm Y) = \text{Var}(X) + \text{Var}(Y) \]

Note: Variances always add (even for subtraction)

General Linear Combination
\[ E(aX + bY) = aE(X) + bE(Y) \]

If X and Y are independent:

\[ \text{Var}(aX + bY) = a^2\text{Var}(X) + b^2\text{Var}(Y) \]

Hypothesis Testing

Null and Alternative Hypotheses

Hypothesis Test Components
  • H₀ (null hypothesis): Statement of no effect or no difference (status quo)
  • H₁ (alternative hypothesis): What you're trying to find evidence for
  • Significance level α: Probability of Type I error (typically 0.05 or 0.01)
  • p-value: Probability of observing data at least as extreme, assuming H₀ is true
  • Test statistic: Value calculated from sample data

Types of Tests

Two-Tailed Test

H₀: parameter = value

H₁: parameter ≠ value

Reject H₀ if p-value < α

One-Tailed Test (Upper)

H₀: parameter ≤ value

H₁: parameter > value

One-Tailed Test (Lower)

H₀: parameter ≥ value

H₁: parameter < value

Errors in Hypothesis Testing

H₀ TrueH₀ False
Reject H₀Type I Error (α)Correct Decision (Power = 1-β)
Fail to Reject H₀Correct DecisionType II Error (β)

Confidence Intervals

Confidence Interval for Population Mean (σ known)
\[ \bar{x} \pm z^* \cdot \frac{\sigma}{\sqrt{n}} \]

Where \( z^* \) is critical value from standard normal

For 95% confidence: \( z^* = 1.96 \)

For 99% confidence: \( z^* = 2.576 \)

Confidence Interval for Population Mean (σ unknown)
\[ \bar{x} \pm t^* \cdot \frac{s}{\sqrt{n}} \]

Use t-distribution with \( n-1 \) degrees of freedom

\( s \) is sample standard deviation

Common Confidence Interval Misconceptions

Wrong: "There's a 95% probability the true mean is in this interval"

Correct: "If we repeated sampling many times, 95% of constructed intervals would contain the true mean"

The parameter is fixed; the interval is random.

Chi-Squared Tests

Chi-Squared Goodness of Fit Test

Chi-Squared Test Statistic
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]

\( O_i \) = observed frequency, \( E_i \) = expected frequency

Degrees of freedom: \( df = k - 1 - p \)

k = number of categories, p = number of estimated parameters

Chi-Squared Test Requirements
  • All expected frequencies ≥ 5
  • Data must be counts/frequencies (not percentages)
  • Categories must be mutually exclusive
  • Always a right-tailed test

Chi-Squared Test for Independence

Expected Frequency for Contingency Table
\[ E_{ij} = \frac{(\text{row total}) \times (\text{column total})}{\text{grand total}} \]

Degrees of freedom: \( df = (r-1)(c-1) \)

r = number of rows, c = number of columns

Correlation and Regression

Correlation Coefficient

Pearson Correlation Coefficient
\[ r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \sqrt{\sum (y_i - \bar{y})^2}} \]

Range: \( -1 \leq r \leq 1 \)

r > 0: positive correlation; r < 0: negative correlation

Linear Regression

Least Squares Regression Line
\[ \hat{y} = a + bx \]

Slope:

\[ b = r \cdot \frac{s_y}{s_x} \]

Intercept:

\[ a = \bar{y} - b\bar{x} \]

Line passes through point \( (\bar{x}, \bar{y}) \)

Interactive Normal Distribution Calculator

Z-Score and Percentile Calculator

Calculate z-score or find percentile for normal distribution

Study Strategies for AA HL Statistics Success

Mastering Probability

  1. Draw Diagrams: Use Venn diagrams, tree diagrams, and tables to visualize probability problems
  2. Practice Bayes' Theorem: Work through many examples until pattern recognition becomes automatic
  3. Understand Independence: Know when events are independent vs dependent—critical for correct calculations
  4. Use Complementary Probability: Often easier to calculate P(not A) than P(A) directly

Mastering Distributions

  1. Know When to Use Each: Create flowchart deciding between binomial, Poisson, normal distributions
  2. Memorize Mean/Variance Formulas: E(X) and Var(X) for each distribution must be automatic
  3. Practice GDC Proficiency: Know exact button sequences for distribution calculations
  4. Check Conditions: Before using approximations, verify conditions are met

Mastering Hypothesis Testing

  1. Write Hypotheses Clearly: State H₀ and H₁ precisely using parameters, not statistics
  2. Understand p-values: p-value is probability of data given H₀ is true, not probability H₀ is true
  3. Know Test Conditions: Each test has requirements—check before applying
  4. Interpret in Context: Always relate statistical conclusion back to real-world situation

Common Mistakes to Avoid

Common ErrorCorrect ApproachExample
Confusing P(A|B) with P(B|A)Use Bayes' theorem to reverse conditional probabilityP(disease|positive test) ≠ P(positive test|disease)
Adding variances when not independentOnly add variances for independent random variablesVar(X-Y) = Var(X) + Var(Y) only if independent
Using wrong distributionCheck conditions: fixed n for binomial, rare events for PoissonPoisson requires small p and large n
Misinterpreting confidence intervalsCI describes procedure, not specific interval"95% of such intervals contain μ" not "95% chance μ is here"
Forgetting degrees of freedomt-tests use n-1, chi-squared varies by test typeChi-squared independence: df = (r-1)(c-1)

Applications in Real-World Contexts

Medical and Health Sciences

  • Clinical Trials: Hypothesis testing to evaluate drug effectiveness
  • Diagnostic Testing: Bayes' theorem for interpreting test results with sensitivity/specificity
  • Epidemiology: Chi-squared tests for disease associations
  • Medical Imaging: Normal distributions for measurement error

Business and Economics

  • Quality Control: Hypothesis testing for manufacturing standards
  • Market Research: Confidence intervals for population parameters
  • Risk Analysis: Probability distributions for financial modeling
  • A/B Testing: Comparing conversion rates between website versions

Science and Engineering

  • Experimental Design: Hypothesis testing for treatment effects
  • Reliability Engineering: Poisson distribution for failure rates
  • Signal Processing: Normal distribution for noise modeling
  • Environmental Science: Regression for pollution trends

Exam Preparation and Strategy

AA HL Statistics Exam Checklist
  • ✓ Master conditional probability and Bayes' theorem
  • ✓ Memorize formulas for E(X) and Var(X) for all distributions
  • ✓ Know when to use binomial, Poisson, normal distributions
  • ✓ Understand linear transformation rules for random variables
  • ✓ Practice hypothesis testing procedure step-by-step
  • ✓ Calculate and interpret confidence intervals correctly
  • ✓ Conduct chi-squared tests with proper degrees of freedom
  • ✓ Interpret correlation and regression in context
  • ✓ Know all GDC functions for statistical calculations
  • ✓ Understand Type I and Type II errors conceptually
  • ✓ Practice interpreting statistical output and p-values
  • ✓ Work complete past papers under timed conditions

Additional RevisionTown Resources

Enhance your AA HL statistics mastery with these comprehensive RevisionTown resources:

Technology and GDC Skills

Essential GDC Functions for AA HL Statistics
  • Binomial Calculations: binompdf and binomcdf for exact and cumulative probabilities
  • Poisson Calculations: poissonpdf and poissoncdf functions
  • Normal Distribution: normalcdf for areas, invNorm for critical values
  • Summary Statistics: 1-Var Stats for mean, standard deviation
  • Regression Analysis: LinReg for equation, r² value
  • Hypothesis Tests: Built-in tests for t-test, chi-squared
  • Confidence Intervals: ZInterval, TInterval functions

Connecting Statistics to Other AA HL Topics

Statistics doesn't exist in isolation—it connects deeply with other AA HL curriculum areas:

  • Calculus: Probability density functions require integration, normal distribution involves exponential functions
  • Functions: Statistical functions model real-world relationships, regression produces function equations
  • Algebra: Manipulating probability expressions, solving for parameters
  • Sequences and Series: Binomial expansion relates to binomial distribution

Conclusion

Mastering statistics and probability is essential for success in IB Mathematics AA HL and provides powerful tools for understanding uncertainty, making data-driven decisions, and conducting rigorous quantitative analysis. The advanced statistical techniques covered in AA HL—from Bayes' theorem and probability distributions through hypothesis testing and confidence intervals to chi-squared tests and regression analysis—form the foundation for university-level statistics, data science, econometrics, and quantitative research in any field.

Success in AA HL statistics requires more than memorizing formulas—it demands conceptual understanding of when to apply each technique, ability to interpret results in context, recognition of assumptions and limitations, and skill in communicating statistical findings clearly. The theoretical rigor of AA HL prepares students for the statistical challenges encountered in STEM degrees, social sciences, medicine, and business at top universities worldwide.

Regular practice with past papers, systematic review of all probability distributions and their properties, consistent application of hypothesis testing procedures, and development of GDC proficiency will build the statistical competence necessary for exam success. Use technology strategically to perform calculations efficiently while maintaining strong conceptual understanding of underlying statistical principles.

Continue building your AA HL mathematics expertise through RevisionTown's comprehensive collection of IB Mathematics resources, practice with interactive calculators, and connect statistical concepts to real-world applications in science, medicine, business, and social research. Master these statistics and probability formulas and techniques, and you'll be well-prepared for IB examinations and the quantitative challenges that await in university studies and professional life.

Tags:
Shares: