IB

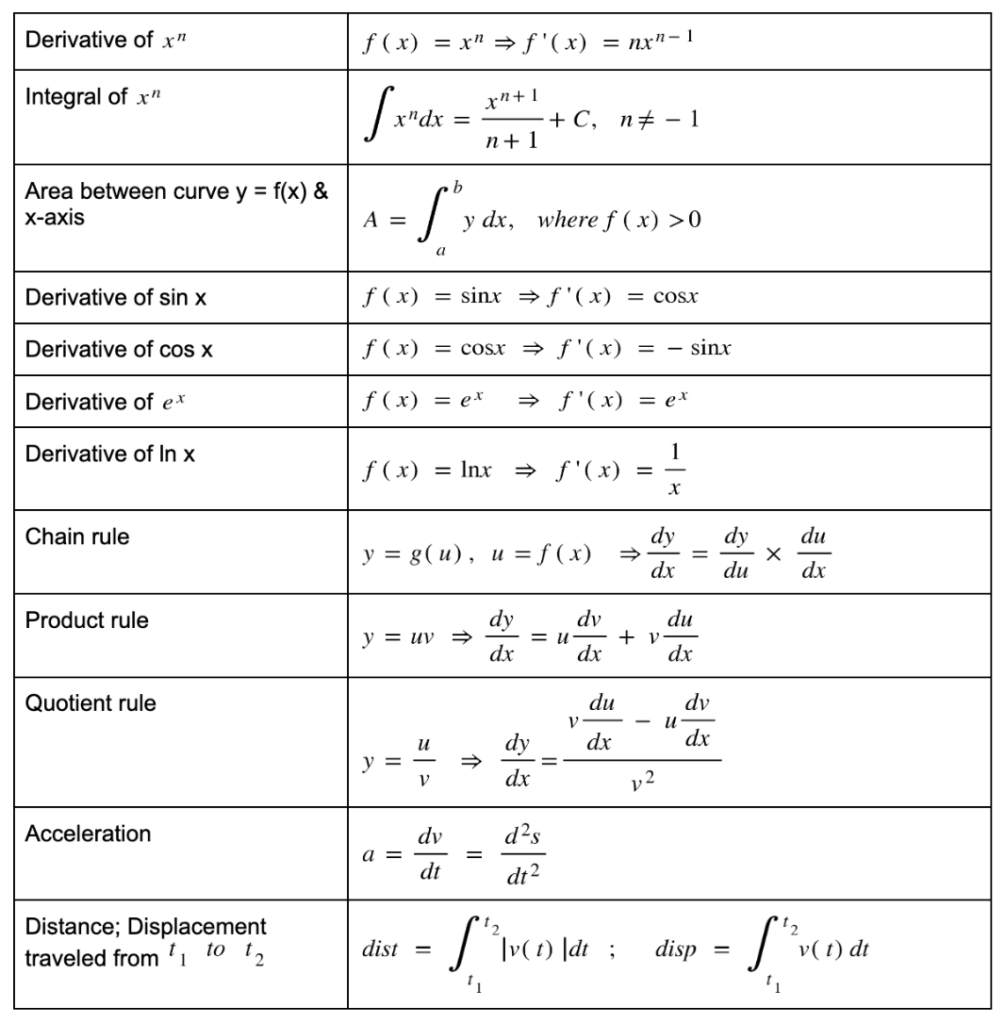
Calculus Formulae AA SL & AA HL

3 years ago
Last Update on February 13, 2026
7 mins
701 Views
Master calculus for IB Math AA SL & HL with our comprehensive guide. Differentiation, integration, chain rule, product rule, kinematics & optimization. Interactive calculator included.
Calculus Formulae reference guide for IB Mathematics Analysis and Approaches Standard Level and Higher Level featuring integral, derivative, and summation symbols
Comprehensive calculus formulae reference for IB Mathematics Analysis and Approaches (AA) at both Standard Level and Higher Level

Calculus Formulae AA SL & AA HL: Complete Guide for IB Math Analysis and Approaches

Welcome to the comprehensive guide for Calculus Formulae in IB Mathematics Analysis and Approaches for both Standard Level and Higher Level students. Calculus forms the foundation of advanced mathematics, enabling us to analyze change, optimize functions, calculate areas and volumes, and model real-world phenomena. This definitive resource covers all essential calculus concepts from basic differentiation and integration through advanced techniques, clearly distinguishing between SL and HL requirements. Whether you're an AA SL student building foundational calculus skills or an AA HL student mastering advanced techniques, this guide provides the complete mathematical toolkit for IB success.

Understanding AA SL vs AA HL Calculus

IB Mathematics AA SL and AA HL share fundamental calculus concepts but differ significantly in depth and breadth. Both courses cover basic differentiation rules, standard integrals, chain rule, product and quotient rules, and applications to kinematics and optimization. However, AA HL extends substantially beyond SL, adding differentiation from first principles, implicit differentiation, related rates, integration by parts, partial fractions, differential equations, Maclaurin series, and advanced applications including volumes of revolution.

Level Indicators Throughout This Guide

Formulas and concepts are labeled with badges to indicate which level requires them:

  • SL & HL - Required for both Standard and Higher Level
  • SL - Standard Level specific content
  • HL - Higher Level only (additional content beyond SL)

Differentiation: Basic Rules

Power Rule SL & HL

The power rule is the most fundamental differentiation rule, applicable to any power of x.

Power Rule
\[ \frac{d}{dx}(x^n) = nx^{n-1} \]

Valid for any real number \( n \)

Example: Power Rule

Differentiate \( f(x) = x^5 \)

Solution: \( f'(x) = 5x^4 \)

Differentiate \( g(x) = \frac{1}{x^2} = x^{-2} \)

Solution: \( g'(x) = -2x^{-3} = -\frac{2}{x^3} \)

Exponential and Logarithmic Derivatives SL & HL

Exponential Function
\[ \frac{d}{dx}(e^x) = e^x \]

The exponential function is its own derivative

Natural Logarithm
\[ \frac{d}{dx}(\ln x) = \frac{1}{x} \]

Defined for \( x > 0 \)

Trigonometric Derivatives SL & HL

Sine and Cosine Derivatives
\[ \frac{d}{dx}(\sin x) = \cos x \] \[ \frac{d}{dx}(\cos x) = -\sin x \]

Note the negative sign for cosine

Tangent Derivative
\[ \frac{d}{dx}(\tan x) = \sec^2 x = \frac{1}{\cos^2 x} \]

Differentiation: Advanced Rules

Chain Rule SL & HL

The chain rule is essential for differentiating composite functions—functions within functions.

Chain Rule Formula
\[ \frac{dy}{dx} = \frac{dy}{du} \times \frac{du}{dx} \]

Where \( y = g(u) \) and \( u = f(x) \)

Alternative form: If \( y = f(g(x)) \), then \( y' = f'(g(x)) \cdot g'(x) \)

Example: Chain Rule

Differentiate \( f(x) = (3x + 2)^5 \)

Solution:

Let \( u = 3x + 2 \), so \( y = u^5 \)

\( \frac{dy}{du} = 5u^4 \) and \( \frac{du}{dx} = 3 \)

\( \frac{dy}{dx} = 5u^4 \times 3 = 15(3x+2)^4 \)

Product Rule SL & HL

Use the product rule when differentiating the product of two functions.

Product Rule Formula
\[ \frac{d}{dx}(uv) = u\frac{dv}{dx} + v\frac{du}{dx} \]

Or: \( (uv)' = u'v + uv' \)

Mnemonic: "First times derivative of second, plus second times derivative of first"

Example: Product Rule

Differentiate \( f(x) = x^2 \sin x \)

Solution:

Let \( u = x^2 \), \( v = \sin x \)

\( u' = 2x \), \( v' = \cos x \)

\( f'(x) = 2x \sin x + x^2 \cos x \)

Quotient Rule SL & HL

Use the quotient rule when differentiating a fraction where both numerator and denominator are functions.

Quotient Rule Formula
\[ \frac{d}{dx}\left(\frac{u}{v}\right) = \frac{v\frac{du}{dx} - u\frac{dv}{dx}}{v^2} \]

Or: \( \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \)

Mnemonic: "Low d-high minus high d-low, over the square of what's below"

Example: Quotient Rule

Differentiate \( f(x) = \frac{x^2}{x+1} \)

Solution:

Let \( u = x^2 \), \( v = x+1 \)

\( u' = 2x \), \( v' = 1 \)

\( f'(x) = \frac{(x+1)(2x) - (x^2)(1)}{(x+1)^2} = \frac{2x^2 + 2x - x^2}{(x+1)^2} = \frac{x^2 + 2x}{(x+1)^2} \)

Integration: Basic Rules

Power Rule for Integration SL & HL

Power Rule for Integration
\[ \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1) \]

Always add constant of integration \( C \) for indefinite integrals

Standard Integrals SL & HL

Essential Standard Integrals
\[ \int \frac{1}{x} \, dx = \ln|x| + C \] \[ \int e^x \, dx = e^x + C \] \[ \int \sin x \, dx = -\cos x + C \] \[ \int \cos x \, dx = \sin x + C \] \[ \int \sec^2 x \, dx = \tan x + C \]
Integration: Reverse of Differentiation

Integration is the inverse operation of differentiation. To verify your integration, differentiate your answer—you should get back the original function (without the constant).

Applications of Differentiation

Kinematics: Position, Velocity, Acceleration SL & HL

Calculus provides the mathematical framework for analyzing motion.

Velocity and Acceleration Formulas
\[ v = \frac{ds}{dt} \quad \text{(velocity is rate of change of position)} \] \[ a = \frac{dv}{dt} = \frac{d^2s}{dt^2} \quad \text{(acceleration is rate of change of velocity)} \]

Where \( s \) = position, \( v \) = velocity, \( a \) = acceleration, \( t \) = time

Example: Kinematics

A particle moves with position \( s(t) = t^3 - 6t^2 + 9t \) meters at time \( t \) seconds.

Find velocity and acceleration at \( t = 2 \).

Solution:

Velocity: \( v(t) = s'(t) = 3t^2 - 12t + 9 \)

\( v(2) = 3(4) - 12(2) + 9 = 12 - 24 + 9 = -3 \) m/s

Acceleration: \( a(t) = v'(t) = 6t - 12 \)

\( a(2) = 6(2) - 12 = 0 \) m/s²

Optimization SL & HL

Differentiation helps find maximum and minimum values of functions—crucial for real-world optimization.

Optimization Strategy
  1. Define the function to optimize
  2. Differentiate and set \( f'(x) = 0 \) to find critical points
  3. Use second derivative test: \( f''(x) > 0 \) → minimum, \( f''(x) < 0 \) → maximum
  4. Check endpoints of domain if restricted

Applications of Integration

Area Under Curves SL & HL

Area Between Curve and x-axis
\[ A = \int_a^b |y| \, dx = \int_a^b |f(x)| \, dx \]

Use absolute value because area is always positive

If curve crosses x-axis, split integral at x-intercepts

Area Between Two Curves
\[ A = \int_a^b [f(x) - g(x)] \, dx \]

Where \( f(x) \geq g(x) \) on interval \( [a, b] \)

Displacement and Distance SL & HL

Distance vs Displacement
\[ \text{Displacement} = \int_{t_1}^{t_2} v(t) \, dt \] \[ \text{Distance} = \int_{t_1}^{t_2} |v(t)| \, dt \]

Displacement can be negative; distance is always positive

Advanced Calculus Concepts (HL Only)

Differentiation from First Principles HL

Derivative from First Principles
\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]

Fundamental definition showing derivative as limit of difference quotient

Implicit Differentiation HL

When y cannot be expressed explicitly as a function of x, use implicit differentiation.

Implicit Differentiation Method
  1. Differentiate both sides with respect to x
  2. When differentiating y terms, multiply by \( \frac{dy}{dx} \) (chain rule)
  3. Collect all \( \frac{dy}{dx} \) terms on one side
  4. Factor out \( \frac{dy}{dx} \) and solve

Integration by Parts HL

Integration by Parts Formula
\[ \int u \, dv = uv - \int v \, du \]

Or: \( \int u \frac{dv}{dx} \, dx = uv - \int v \frac{du}{dx} \, dx \)

Use LIATE to choose u: Logarithmic, Inverse trig, Algebraic, Trigonometric, Exponential

Volume of Revolution HL

Volume About x-axis
\[ V = \pi \int_a^b y^2 \, dx = \pi \int_a^b [f(x)]^2 \, dx \]
Volume About y-axis
\[ V = \pi \int_c^d x^2 \, dy = \pi \int_c^d [g(y)]^2 \, dy \]

Interactive Slope Calculator

Slope and Average Rate of Change Calculator

Calculate the slope between two points

Study Strategies for Calculus Success

For AA SL Students

  1. Master Basic Rules First: Power rule, exponential, logarithmic, and trig derivatives must become automatic
  2. Practice Chain Rule: 80% of calculus problems require chain rule. Practice identifying composite functions
  3. Memorize Standard Integrals: Create flashcards for all standard integrals and their derivatives
  4. Understand Applications: Connect calculus to kinematics and optimization—these appear frequently on exams
  5. Use GDC Effectively: Know how to find derivatives and integrals numerically on your calculator

For AA HL Students

  1. Build on SL Foundations: Ensure complete mastery of all SL concepts before tackling HL content
  2. Practice Integration by Parts: Use LIATE rule consistently. Attempt problems multiple times
  3. Master Implicit Differentiation: Practice identifying when to use this technique
  4. Understand Differential Equations: Learn separation of variables and integrating factor methods
  5. Work Through Past Papers: HL Paper 3 contains extended calculus problems requiring synthesis of multiple techniques

Common Mistakes to Avoid

Common ErrorCorrect ApproachExample
Forgetting chain ruleAlways check for composite functions\( \frac{d}{dx}(e^{2x}) = 2e^{2x} \), not \( e^{2x} \)
Missing absolute value in areaUse \( |y| \) when curve goes below x-axisArea is always positive
Omitting integration constantAlways add \( +C \) for indefinite integrals\( \int x \, dx = \frac{x^2}{2} + C \)
Wrong sign in trig derivativesMemorize: \( \frac{d}{dx}(\cos x) = -\sin x \)Cosine derivative is negative
Confusing displacement and distanceDistance uses absolute value of velocity\( d = \int |v(t)| dt \)

Key Differences: SL vs HL

TopicAA SLAA HL
Basic DifferentiationPower, exponential, log, trigSame, plus from first principles
Advanced DifferentiationChain, product, quotient rulesSame, plus implicit differentiation
Basic IntegrationPower rule, standard integralsSame foundations
Advanced IntegrationSubstitution methodIntegration by parts, partial fractions
ApplicationsArea, kinematics, optimizationVolume of revolution, differential equations
SeriesNot requiredMaclaurin series

Exam Preparation Tips

Calculus Exam Checklist

For Both SL & HL:

  • ✓ Memorize all standard derivatives and integrals
  • ✓ Practice chain rule until automatic
  • ✓ Know when to use product vs quotient rule
  • ✓ Understand kinematics applications (velocity, acceleration)
  • ✓ Practice area calculations with curves crossing x-axis
  • ✓ Master optimization problems (max/min)
  • ✓ Use GDC to verify numerical answers

Additional for HL:

  • ✓ Practice differentiation from first principles
  • ✓ Master integration by parts with LIATE
  • ✓ Understand implicit differentiation method
  • ✓ Solve differential equations (separation, integrating factor)
  • ✓ Calculate volumes of revolution
  • ✓ Memorize standard Maclaurin series

Additional RevisionTown Resources

Enhance your calculus mastery with these comprehensive RevisionTown resources:

Real-World Applications of Calculus

Physics and Engineering

  • Motion Analysis: Position, velocity, acceleration relationships in projectile motion and circular motion
  • Optimization: Minimizing material costs, maximizing efficiency in design
  • Rates of Change: Temperature change, population growth, radioactive decay
  • Work and Energy: Calculating work done by variable forces

Economics and Business

  • Marginal Analysis: Marginal cost, marginal revenue, marginal profit
  • Optimization: Maximizing profit, minimizing cost
  • Elasticity: Price elasticity of demand using derivatives

Biology and Medicine

  • Population Dynamics: Modeling population growth and decay
  • Drug Concentration: Rates of drug absorption and elimination
  • Epidemic Modeling: Spread of diseases using differential equations

Technology and Calculator Skills

Essential GDC Functions for Calculus
  • Numerical Differentiation: Find \( f'(x) \) at specific points to verify analytical work
  • Numerical Integration: Calculate \( \int_a^b f(x) dx \) to check definite integrals
  • Graphing: Visualize functions and identify critical points
  • Table Mode: Generate value tables for analysis
  • Equation Solver: Find where \( f'(x) = 0 \) for optimization
  • Trace Function: Find exact coordinates for area calculations

Conclusion

Calculus forms the cornerstone of IB Mathematics AA at both Standard and Higher Level, providing powerful tools for analyzing change, optimizing functions, and modeling real-world phenomena. Whether you're an AA SL student building foundational skills or an AA HL student tackling advanced techniques, mastery of calculus concepts opens doors to success in mathematics, science, engineering, economics, and countless other fields.

Success in calculus requires more than memorizing formulas—it demands understanding when and how to apply each technique, recognizing patterns in problems, and building computational fluency through extensive practice. The differentiation between SL and HL content reflects increasing mathematical sophistication, with HL students developing the advanced analytical skills necessary for STEM degrees at top universities.

Regular practice with past papers, systematic review of all standard derivatives and integrals, and consistent application of rules will build the automaticity necessary for exam success. Use your GDC strategically to verify numerical work while maintaining strong analytical skills for symbolic manipulation.

Continue building your AA mathematics expertise through RevisionTown's comprehensive collection of IB Mathematics resources, practice with interactive calculators, and connect calculus concepts to real-world applications. Master these calculus formulas and techniques, and you'll be well-prepared for IB examinations and the mathematical challenges that await in university studies.

Tags:
Shares: