The Limit of a Function and One Sided Limits

Definition of Limit

The Statement

$\lim_{x \to c} f (x) = L$

means f approaches the limit L as x approaches c.

Which is read “the limit of f(x), as x approaches c, equals L.”

Basic Limits

1. If f is the constant function f(x) = k, then for any value of c,

$\lim_{x \to c} f (x) = \lim_{x \to c} k = k$

2. If f is the polynomial function f(x) = xⁿ, then for any value of c,

\lim_{x \to c} f (x) = \lim_{x \to c} x^{n} = c^{n}

Finding Limits Graphically

Consider the graph of the function

$f (x) = \frac{x^{3} + 1}{x + 1}$

The given function is defined for all real numbers x except x = −1. The graph of f is a parabola with the point (−1, 3) removed as shown below. Even though f(−1) is not defined, we can make the value of f(x) as close to 3 as we want by choosing an x close enough to −1.

Although f(x) is not defined when x=−1, the limit of f(x) as x approaches −1 is 3, because the definition of a limit says that we consider values of x that are close to c, but not equal to c.

One Sided Limits

The right-hand Limit means that x approaches c from values greater than c.

This limit is denoted as

$\lim_{x \to c^{+}} f (x) = L$

The left-hand limit means that x approaches c from values less than c.

This limit is denoted as

$\lim_{x \to c^{-}} f (x) = L$

The Existence of a Limit

The limit of f(x) as x approaches c is L if and only if

$\lim_{x \to c^{+}} f (x) = L$

and

$\lim_{x \to c^{-}} f (x) = L$

Limits That Fail to Exits

Some limits that fail to exits are illustrated below.

The left limit and the right limit is different.

$\begin{array}{l} \lim_{x \to 0} \frac{|x|}{x} = 1, i f x > 0 a n d \\ \lim_{x \to 0} \frac{|x|}{x} = - 1, i f x < 0 \end{array}$

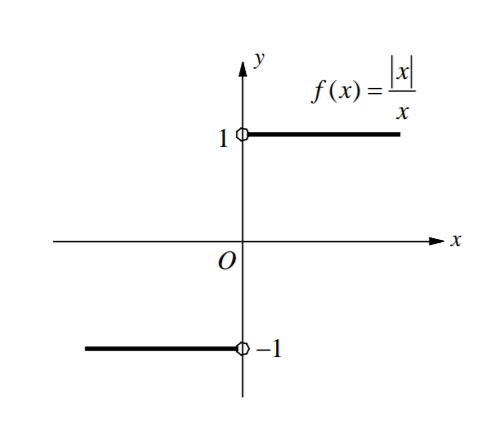
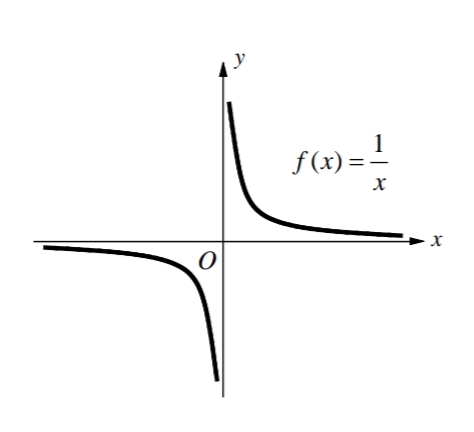
As x approaches 0 from from the right or the left, f(x) increases or decreases without bound.

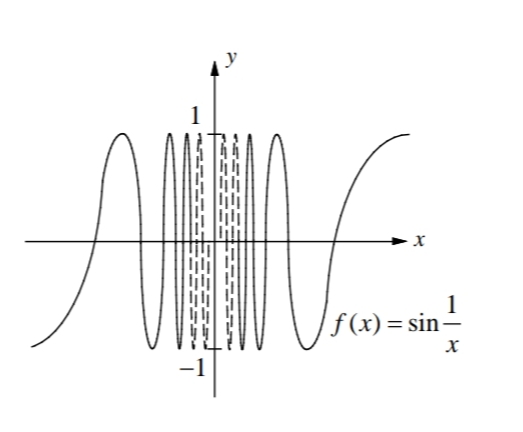
The values of f(x) oscillate between −1 and 1 infinitely often as x approaches 0.

Example 1. Find the limit.

$\begin{array}{l} (a) \lim_{x \to 2} (7) \\ (b) \lim_{x \to - 1} (x^{3} - 2 x) \\ (c) \lim_{x \to 0} \frac{\sin x}{x} \end{array}$

Solution:

$\begin{array}{l} (a) \lim_{x \to 2} (7) = 7 \\ b e c a u s e \\ \lim_{x \to c} k = k \\ (b) \lim_{x \to - 1} (x^{3} - 2 x) \\ = (^{- 1) 3} - 2 (- 1) = 1 \\ b e c a u s e \\ \lim_{x \to c} x^{n} = c^{n} \end{array}$

$Graph y = \frac{\sin x}{x}$

using a graphing calculator. The limit of f(x) = (sin x)/x as x approaches 0 is 1.

Example 2. The Graph of the function f is shown in the figure below. Find the limit or value of the function at a given point.

\begin{array}{l} (a) \lim_{x \to 3^{-}} f (x) \\ (b) \lim_{x \to 3^{+}} f (x) \\ (c) \lim_{x \to 3} f (x) \\ (d) \lim_{x \to 6} f (x) \\ (e) f (3) \\ (f) f (6) \end{array}

Solution:

$\begin{array}{l} (a) \lim_{x \to 3^{-}} f (x) = 0 \\ (b) \lim_{x \to 3^{+}} f (x) = 3 \\ (c) \lim_{x \to 3} f (x) \\ does not exists since \\ \lim_{x \to 3^{-}} f (x) \neq \lim_{x \to 3^{+}} f (x) \\ (d) \lim_{x \to 6} f (x) = 3, \\ b e c a u s e \\ \lim_{x \to 6^{-}} f (x) = 3 = \lim_{x \to 6^{+}} f (x) \\ (e) f (3) = 0 \\ (f) f (6) = 1 \end{array}$