Mathematics often feels like a vast landscape of abstract concepts and intricate theories. However, at its core, it’s a tool that helps us make sense of the world around us. Two fundamental ideas in this mathematical journey are polynomial functions and rates of change. Whether you’re a student grappling with algebra or a curious mind seeking deeper understanding, grasping these concepts is both fascinating and immensely rewarding. Let’s delve into the world of polynomial functions and explore how they interplay with rates of change.
What Are Polynomial Functions?
At its simplest, a polynomial function is an expression consisting of variables (also known as indeterminates) and coefficients, combined using only addition, subtraction, multiplication, and non-negative integer exponents of variables. The general form of a polynomial function in one variable xxx is:


Exploring Rates of Change
At its essence, the rate of change measures how one quantity changes in relation to another. In mathematics, particularly calculus, rates of change are quantified using derivatives.
Average vs. Instantaneous Rate of Change
Average Rate of Change:
- It measures the change in the function’s value over a specific interval.
- For a function P(x), between x=a and x=b:
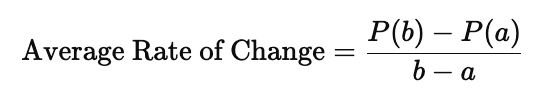
- For the linear polynomial P(x)=3x+2P(x) = 3x + 2P(x)=3x+2, the average rate of change between any two points is 3, which is the slope of the line.
Instantaneous Rate of Change:
- It measures how the function’s value changes at an exact point.
- Mathematically, it’s the derivative of the function at that point.
- For P(x)=x^2, the instantaneous rate of change at x=3 is:
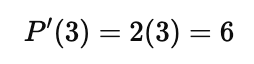
Real-World Applications
Understanding polynomial functions and their rates of change is crucial across various fields:
Physics:
- Motion: Position, velocity, and acceleration can be modeled using polynomials. For example, if position s(t) is a polynomial function of time t, the derivative s′(t) gives velocity, and s′′(t) provides acceleration.
Economics:
- Cost and Revenue Models: Polynomial functions can represent cost, revenue, and profit over time or quantity. Derivatives help determine optimal production levels by analyzing marginal costs and revenues.
Engineering:
- Design and Optimization: Polynomial equations model various engineering systems, and understanding their rates of change aids in optimizing performance and ensuring stability.
Biology:
- Population Dynamics: Growth rates of populations can be modeled using polynomial functions, with derivatives indicating how quickly populations are increasing or decreasing.
Visualizing the Concepts
Visual aids can significantly enhance our understanding of these mathematical concepts. Consider the following graphs:
Polynomial Function and Its Derivative:
In this graph, the blue curve represents the polynomial function P(x)=x^3−3x^2+2x, and the orange curve represents its derivative P'(x) = 3x^2 – 6x + 2. The points where the derivative crosses the x-axis indicate local maxima or minima of the original polynomial.
Rates of Change:
Here, the green line shows the average rate of change over an interval, while the red tangent line illustrates the instantaneous rate of change at a specific point.
Conclusion
Polynomial functions and rates of change are intertwined concepts that form the backbone of many mathematical models and real-world applications. By understanding polynomial functions, we gain the ability to model complex behaviors and phenomena. Delving into rates of change, particularly through derivatives, allows us to analyze how these models behave dynamically.
Whether you’re tackling algebra problems, exploring calculus, or applying these concepts in various scientific fields, grasping the relationship between polynomial functions and their rates of change equips you with powerful tools to interpret and influence the world around you.
Embrace the beauty of these mathematical concepts, and you’ll find that what once seemed abstract becomes a clear lens through which to view and solve real-world challenges.


