Area Calculator
Use this area calculator to easily calculate the area of common shapes like a square, rectangle, triangle, circle, parallelogram, trapezoid, ellipse (oval), regular octagon, and sector of a circle. Formulas and explanations on finding the area of any shape can be found below the tool.
(Here you can show an image or schematic of the chosen shape.)
How to calculate the area of any shape?
Each geometrical figure has a different formula for calculating its area, and different required measurements that need to be known. See below for details on each individual one this area calculator supports, including the formula used. When taking measurements or reading plans, make sure all measurements are in the same units, or convert them to the same unit to get a valid result. The result is always a squared unit, e.g. square centimeters, square kilometers, square inches, square feet, square miles…
Finding the area of various internal surfaces such as floors and walls has applications in construction and home decoration. An example application of area calculation is to find the number of tiles to purchase or the amount of paint required to paint a wall, both of which need to be done via finding a square footage. Land area calculations are used in land management, agriculture, biology, ecology, and many other disciplines. One may also need to calculate the area of different surfaces in physics, chemistry, engineering, and other applied disciplines.
Area of a square
The formula for the area of a square is side2, as seen in the figure below:

This is the simplest figure to calculate the area of as it requires just a single measurement using a ruler, a tape measure, or a similar device. However, since in most practical situations you need to measure both sides before you know it is a square, it will take the same number of measurements as a rectangular-shaped surface.
Area of a rectangle
The formula for the area of a rectangle is width x height, as seen in the figure below:

To find the area, you would either be given or would have to take two measurements: the width and the height, and just multiply them together. It is one of the easiest figures to compute the area of.
In many cases irregular shapes that require an area calculation would be broken down into a series of rectangles. By summing these rectangular areas an irregularly-shaped area can be approximately calculated.
Area of a triangle
The formula for the area of a triangle is height x π x (radius / 2)2, where (radius / 2) is the radius of the base (d = 2 x r), so another way to write it is height x π x radius2. Visual in the figure below:
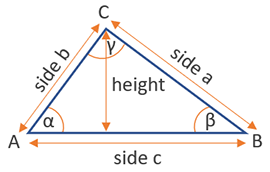
Despite the simplicity of the above equation, in specific situations you may not know these two exact measurements. There are multiple rules to calculate a triangle’s area: SSS (side-side-side), SAS (two sides and the included angle), SSA (two sides and a non-included angle), ASA (two angles and the included side), each with its own equation. For right-angled triangles you can calculate the area by knowing the hypotenuse and the height towards it. All of these are supported by this online area calculator.
Area of a circle
The formula to find the area of a circle is π x radius2, but the diameter of the circle is d = 2 x r, so another way to write the equation is as π x (diameter / 2)2. Here is what the measurement looks like:

In order to find the area of a circle you need to know only its radius. However, in most practical situations it is easier to calculate the diameter which is why our calculator requires the diameter as an input. If you know the radius instead, just multiply it by two to get the diameter.
Area of a parallelogram
The formula for the area of a parallelogram is width x height, as seen in the figure below:

It can be shown through simple mathematical transformations that a parallelogram’s area can be viewed as the area of a rectangle with its sides being equal to any side of the parallelogram and the height to it. The formula to find the area of a parallelogram is therefore also a simple multiplication.
Area of a trapezoid
To find the area of a trapezoid use the equation (base 1 + base 2) / 2 x height. The inputs are as seen in the figure below:
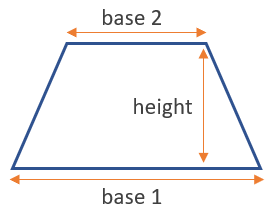
By definition, the bases are always parallel to each other so it is easy to identify them. This is one of the more complex formulas, but still pretty manageable, especially with the help of an area finder. A trapezoid can be transformed to a rectangle by knowing the length of each base and its height, so these are the minimum required measurements.
Area of an ellipse (oval)
The formula for the area of an ellipse is π x major radius x minor radius with measurements as shown:

The area of an oval is found similarly to that of a circle, but since it has two radiuses, the equation and required measurements are slightly different. With an oval one needs to measure the two diameters and divide by two to get the two radiuses.
Area of a sector
The formula for the area of a sector is (angle / 360) x π x radius, but the diameter of the circle is d = 2 x r, so another way to write it is (angle / 360) 2 x π x (diameter / 2). A graph showing the needed measurements is below:

Since a sector is just a slice from a circle, the formula to find its area is quite similar to the one used for the area of a circle. The only difference is the additional math required to calculate what part of the circle the sector covers. The radius is easy to measure with a ruler, a tape measure, a measuring wheel, a line measure, a laser tape measure, and a variety of other options. Getting the angle right, however, requires using an angle finder which might be a prerequisite for finding the area of a sector if its measurement is not given.
Area of an octagon
The area of an octagon of regular shape can be found using the formula 2 · (1 + √2) · side2, where a side is as shown below:

It only requires a single measurement, granted that it is already known that the figure is, indeed, a regular octagon. Otherwise one needs to measure all sides first to confirm that they are all equal, before proceeding to calculate its area.
Applications for an area calculator
A specialized calculator is obviously handy if you have some geometry homework or if you are allowed to use online tools in class. Other than that, a dedicated calculator might be needed by people involved in certain crafts, engineering, and even in many arts. Many DIY home projects, garden projects, etc. also end up requiring that you calculate one or more areas so you know how much material to purchase, e.g. as in a paint calculator.

