📚 Partial Fractions Study Notes
Complete Guide for IB Mathematics AA HL
Theory, Examples & Interactive Practice
📖 Study Guide Navigation
📌 What are Partial Fractions?
Partial fractions are the reverse process of adding or subtracting algebraic fractions. Instead of combining fractions into a single fraction, we decompose a complex fraction into simpler parts.
This technique is essential for integration, differential equations, and simplifying complex rational expressions in IB Mathematics AA HL.
🎯 Why Study Partial Fractions in IB?
- Integration Technique: Essential for integrating rational functions that don't fit standard forms
- Exam Weight: Regular appearance in IB Mathematics AA HL Paper 1 and Paper 2 (typically 4-8 marks)
- Prerequisites: Requires strong factoring skills, algebraic manipulation, and equation solving
- Applications: Used in solving differential equations, Laplace transforms, and complex analysis
- Connection to Other Topics: Links to polynomial division, logarithmic integration, and series expansions
🔢 Types of Partial Fractions
The form of partial fractions depends on the factors in the denominator. Here are the main types you'll encounter in IB Mathematics:
Type 1: Distinct Linear Factors
Where A and B are constants to be determined.
Type 2: Repeated Linear Factors
Each power requires a separate term in the decomposition.
Type 3: Quadratic Factor (Irreducible)
Quadratic factors require linear numerators (Bx + C).
Type 4: General Repeated Factor
For (ax + b)ⁿ, include terms up to power n.
⚙️ Step-by-Step Method for Partial Fractions
Follow this systematic approach for any partial fraction problem:
STEP 1: Check if Proper Fraction
Ensure the degree of the numerator is less than the degree of the denominator. If not, perform polynomial long division first to make it proper.
Proper: (3x + 5)/(x² + 2x - 3) ✓ Improper: (x³ + 2)/(x² - 1) ✗
STEP 2: Factorize the Denominator
Completely factorize the denominator into linear and/or quadratic factors. Simplify if any common factors exist between numerator and denominator.
Example: 2x² - 5x - 3 = (2x + 1)(x - 3)
STEP 3: Set Up Partial Fractions
Write the fraction as a sum of partial fractions with unknown constants (A, B, C, etc.) in the numerators. The form depends on the type of factors in the denominator.
Example: P(x)/((2x + 1)(x - 3)) = A/(2x + 1) + B/(x - 3)
STEP 4: Eliminate Fractions
Multiply both sides by the common denominator (the original denominator) to eliminate all fractions. This creates an identity that must be true for all values of x.
Example: 3x + 5 = A(x - 3) + B(2x + 1)
STEP 5: Find Constants (Method 1 - Substitution)
Substitute strategic values of x (usually the roots of the denominator factors) to create simple equations for A, B, C, etc.
Let x = 3: 3(3) + 5 = A(0) + B(7) → B = 2
Let x = -1/2: 3(-1/2) + 5 = A(-7/2) + B(0) → A = -1
STEP 5: Find Constants (Method 2 - Comparing Coefficients)
Alternatively, expand the right side and compare coefficients of like terms (x², x, constants) on both sides to form simultaneous equations.
Coefficient of x: 3 = A + 2B
Constant term: 5 = -3A + B
STEP 6: Write Final Answer
Substitute the values of constants back into the partial fractions form. Always verify by combining the fractions to check you get the original expression.
📐 Case 1: Distinct Linear Factors
📝 Worked Example 1
Express (7x + 13)/(x² + x - 6) in partial fractions.
x² + x - 6 = (x + 3)(x - 2)
(7x + 13)/((x + 3)(x - 2)) = A/(x + 3) + B/(x - 2)
7x + 13 = A(x - 2) + B(x + 3)
7(2) + 13 = A(0) + B(5)
27 = 5B
B = 27/5
7(-3) + 13 = A(-5) + B(0)
-8 = -5A
A = 8/5
📝 Worked Example 2
Decompose (5x - 1)/(x² - 4) into partial fractions.
x² - 4 = (x - 2)(x + 2)
(5x - 1)/((x - 2)(x + 2)) = A/(x - 2) + B/(x + 2)
5x - 1 = A(x + 2) + B(x - 2)
5(2) - 1 = A(4) + B(0)
9 = 4A → A = 9/4
5(-2) - 1 = A(0) + B(-4)
-11 = -4B → B = 11/4
🔁 Case 2: Repeated Linear Factors
When a linear factor appears more than once (e.g., (x + 2)²), we need separate terms for each power up to the highest power.
📝 Worked Example 3
Express (20x + 35)/(x + 4)² in partial fractions.
(20x + 35)/(x + 4)² = A/(x + 4) + B/(x + 4)²
20x + 35 = A(x + 4) + B
20x + 35 = Ax + 4A + B
Coefficient of x: A = 20
Constant term: 4A + B = 35
4(20) + B = 35
B = -45
📝 Worked Example 4
Decompose (3x² - 2x + 1)/((x - 1)²(x + 2)) into partial fractions.
(3x² - 2x + 1)/((x - 1)²(x + 2)) = A/(x - 1) + B/(x - 1)² + C/(x + 2)
3x² - 2x + 1 = A(x - 1)(x + 2) + B(x + 2) + C(x - 1)²
3(1)² - 2(1) + 1 = B(3)
2 = 3B → B = 2/3
3(-2)² - 2(-2) + 1 = C(-3)²
17 = 9C → C = 17/9
1 = A(-1)(2) + B(2) + C(1)
1 = -2A + 2(2/3) + 17/9
1 = -2A + 4/3 + 17/9
-2A = 1 - 12/9 - 17/9 = -20/9
A = 10/9
📊 Case 3: Irreducible Quadratic Factors
When the denominator contains a quadratic factor that cannot be factored further (discriminant < 0), the numerator must be linear (Ax + B), not just a constant.
📝 Worked Example 5
Express 10/((x - 1)(x² + 9)) in partial fractions.
x² + 9 has discriminant = 0² - 4(1)(9) = -36 < 0
Therefore irreducible (cannot be factored over real numbers)
10/((x - 1)(x² + 9)) = A/(x - 1) + (Bx + C)/(x² + 9)
10 = A(x² + 9) + (Bx + C)(x - 1)
10 = A(10) + 0
A = 1
10 = Ax² + 9A + Bx² - Bx + Cx - C
10 = (A + B)x² + (-B + C)x + (9A - C)
Coefficient of x²: 0 = A + B → B = -1
Coefficient of x: 0 = -B + C → C = -1
Constant: 10 = 9A - C → 10 = 9(1) - (-1) = 10 ✓
or: = 1/(x - 1) - (x + 1)/(x² + 9)
⚡ Case 4: Improper Fractions
An improper fraction has a numerator with degree ≥ denominator degree. Before decomposing, we must perform polynomial long division.
Then apply partial fractions only to the proper fraction (Remainder/Q(x))
📝 Worked Example 6
Express (x³ + 2x² + 3)/(x² - 1) as partial fractions.
Numerator degree = 3, Denominator degree = 2
Since 3 > 2, this is IMPROPER - must divide first!
Dividing x³ + 2x² + 3 by x² - 1:
_______________
x² - 1 | x³ + 2x² + 0x + 3
x³ + 0x² - x
_______________
2x² + x + 3
2x² + 0x - 2
_______________
x + 5
Result: (x³ + 2x² + 3)/(x² - 1) = x + 2 + (x + 5)/(x² - 1)
(x + 5)/(x² - 1) = (x + 5)/((x - 1)(x + 1)) = A/(x - 1) + B/(x + 1)
x + 5 = A(x + 1) + B(x - 1)
Let x = 1: 6 = 2A → A = 3
Let x = -1: 4 = -2B → B = -2
🔗 Application: Integration with Partial Fractions
🎯 Why Partial Fractions for Integration?
Many rational functions cannot be integrated directly. Partial fractions break them into simpler forms that integrate to logarithms and inverse trigonometric functions.
Key Integration Results
After partial fraction decomposition, integrate each term separately using these standard forms.
📝 Integration Example
Evaluate ∫ (7x + 13)/(x² + x - 6) dx
(7x + 13)/(x² + x - 6) = (8/5)/(x + 3) + (27/5)/(x - 2)
∫ [(8/5)/(x + 3) + (27/5)/(x - 2)] dx
= (8/5)ln|x + 3| + (27/5)ln|x - 2| + C
= (1/5)ln|(x + 3)8(x - 2)27| + C
✍️ Interactive Practice Problems
Test your understanding with these IB-style problems. Enter your answer and check immediately!
Problem 1: Distinct Linear Factors
Give your answer in the form: A/(x - 1) + B/(x + 1)
Enter A and B:
📖 Complete Solution
Problem 2: Repeated Linear Factors
Give your answer in the form: A/(x + 1) + B/(x + 1)²
Enter A and B:
📖 Complete Solution
Coefficient of x: A = 3
Constant: A + B = 1 → 3 + B = 1 → B = -2
Problem 3: Three Linear Factors
Give your answer in the form: A/(x - 1) + B/(x + 1) + C/(x + 2)
Enter A, B, and C:
📖 Complete Solution
2x² + x + 1 = A(x + 1)(x + 2) + B(x - 1)(x + 2) + C(x - 1)(x + 1)
2(1) + 1 + 1 = A(2)(3) → 4 = 6A → A = 2/3
2(1) - 1 + 1 = B(-2)(1) → 2 = -2B → B = -1
2(4) - 2 + 1 = C(-3)(-1) → 7 = 3C → C = 7/3
Problem 4: Mixed Factors Challenge
Give your answer in the form: A/(x + 1) + B/(x + 1)² + C/(x - 2)
Enter A, B, and C:
📖 Complete Solution
x² + 3x + 5 = A(x + 1)(x - 2) + B(x - 2) + C(x + 1)²
1 - 3 + 5 = B(-3) → 3 = -3B → B = -1
4 + 6 + 5 = C(9) → 15 = 9C → C = 5/3
5 = A(1)(-2) + B(-2) + C(1)
5 = -2A - 2(-1) + 5/3
5 = -2A + 2 + 5/3 → -2A = 5 - 2 - 5/3 = 4/3
A = -2/3
⚠️ Common Mistakes to Avoid
❌ Mistake 1: Wrong Form for Repeated Factors
Wrong: P(x)/(x + 2)² = A/(x + 2)²
Correct: P(x)/(x + 2)² = A/(x + 2) + B/(x + 2)²
❌ Mistake 2: Constant for Quadratic Factors
Wrong: P(x)/(x² + 4) = A/(x² + 4)
Correct: P(x)/((x - 1)(x² + 4)) = A/(x - 1) + (Bx + C)/(x² + 4)
❌ Mistake 3: Forgetting to Factor
Don't decompose before factoring denominator completely
Always factor first: x² - 4 = (x - 2)(x + 2)
❌ Mistake 4: Improper Fractions
Decomposing directly when deg(numerator) ≥ deg(denominator)
Must perform polynomial division first!
🎓 IB Exam Strategy & Tips
📝 Exam Technique
- Show All Steps: IB examiners award method marks. Always show factorization, setup, and calculations clearly
- Check Your Work: Quickly verify by combining your partial fractions back to the original - catches arithmetic errors
- Time Management: Partial fraction questions are typically 4-8 marks and should take 5-10 minutes
- Use Calculator Wisely: GDC can verify your final answer by evaluating both forms at a test value
- Common Point Values: M1 for form, M1 for eliminating fractions, A1 for each constant
🎯 What Examiners Look For
- Correct Form: Setting up the right partial fractions structure (M1 mark)
- Valid Method: Either substitution or coefficient comparison consistently applied
- Accurate Arithmetic: Correct calculation of constants (A1 marks)
- Simplified Answer: Final answer with fractions in lowest terms
- Follow-Through: Integration questions may allow marks even if partial fractions have errors
📌 Quick Reference Summary
- Distinct Linear: (ax + b)(cx + d) → A/(ax + b) + B/(cx + d)
- Repeated Linear: (ax + b)² → A/(ax + b) + B/(ax + b)²
- Irreducible Quadratic: (ax + b)(cx² + dx + e) → A/(ax + b) + (Bx + C)/(cx² + dx + e)
- Improper Fractions: Perform polynomial division first
- Solving Methods: Substitution (faster) or comparing coefficients (systematic)
- Applications: Integration of rational functions, differential equations
👨🏫 About the Author
Adam
Co-Founder @ RevisionTown
Math Expert in Various Curricula: IB, AP, GCSE, IGCSE, A-Levels
Specializing in helping IB students master challenging topics like partial fractions through clear explanations, worked examples, and interactive practice. Committed to exam success through understanding, not just memorization.
💪 Master partial fractions with practice and persistence!
Visit RevisionTown.com for more IB Mathematics resources
Solving partial fractions problems
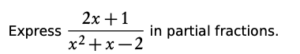
- Determine which linear terms make up the denominator
x2 + x − 2 = (x − 1)(x + 2)
2. Equate the fraction to sum of two fractions with unknown constants as numerators and the linear terms as denominators
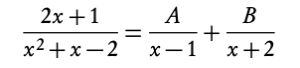
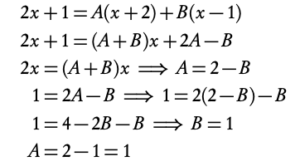
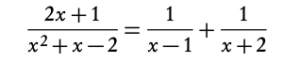
Frequently Asked Questions: Partial Fractions
What is Partial Fraction Decomposition?
Partial fraction decomposition is a mathematical technique used to break down a rational expression (a fraction where the numerator and denominator are polynomials) into a sum of simpler fractions, called partial fractions.
Why is Partial Fraction Decomposition used?
Its primary use is in calculus, specifically for integrating rational functions. Breaking down a complex rational function into simpler partial fractions makes the integration process much easier, as the resulting terms can often be integrated using basic rules (like logarithms or arctangents).
When should I use Partial Fraction Decomposition?
You use partial fraction decomposition when you need to integrate a rational function (a polynomial divided by another polynomial) where the degree of the numerator is less than the degree of the denominator (a proper fraction). If the degree of the numerator is greater than or equal to the denominator (an improper fraction), you first perform polynomial long division.
How do you do Partial Fraction Decomposition?
The general steps are:
- Check if the fraction is proper. If not, divide the polynomials first.
- Factor the denominator completely into linear factors (ax+b) and irreducible quadratic factors (ax²+bx+c where b²-4ac < 0).
- Set up the form of the partial fraction decomposition based on the factors.
- Solve for the unknown constants (like A, B, C) in the numerator(s) using methods such as equating coefficients or substituting roots of the denominator.
How do I set up the partial fractions for different types of factors?
The setup depends on the factors of the denominator:
- Linear Distinct Factors (ax+b): For each distinct linear factor, use a term like A / (ax+b).
- Repeated Linear Factors ((ax+b)ⁿ): For a factor repeated n times, use a sum of n terms: A₁ / (ax+b) + A₂ / (ax+b)² + ... + An / (ax+b)ⁿ.
- Irreducible Quadratic Factors (ax²+bx+c): For each distinct irreducible quadratic factor, use a term like (Ax+B) / (ax²+bx+c).
- Repeated Irreducible Quadratic Factors ((ax²+bx+c)ⁿ): For a factor repeated n times, use a sum of n terms: (A₁x+B₁) / (ax²+bx+c) + (A₂x+B₂) / (ax²+bx+c)² + ... + (Anx+Bn) / (ax²+bx+c)ⁿ.
How do I solve for the unknown constants (A, B, etc.)?
After setting up the form, multiply both sides of the equation by the original denominator to clear the denominators. Then you can solve for the constants using two main methods:
- Method of Equating Coefficients: Expand the right side of the equation and group terms by powers of x (x², x, constant). Equate the coefficients of corresponding powers of x on both sides of the equation to get a system of linear equations. Solve this system for the constants.
- Method of Substitution (Heaviside Cover-Up Method): Substitute the roots of the original denominator (the values of x that make the denominator zero) into the equation (after clearing denominators). This can directly give you the values of some constants, especially for distinct linear factors. For irreducible quadratic factors or repeated roots, a combination of methods might be needed.
How do I integrate using Partial Fractions?
Once you have decomposed the original rational function into a sum of simpler partial fractions, you integrate each partial fraction separately. The integration of these simpler forms is standard:
- Terms like A / (ax+b) integrate to (A/a) ln|ax+b| + C.
- Terms like B / (ax+b)ⁿ (n ≠ 1) integrate using the power rule: B ∫ (ax+b)-n dx.
- Terms like (Ax+B) / (ax²+bx+c) often require splitting into two integrals: one that integrates to a logarithm (related to the derivative of the denominator) and one that integrates to an arctangent.
Sum the results of integrating each partial fraction to get the final integral of the original rational function.
What if the rational function is improper (degree of numerator ≥ degree of denominator)?
If the degree of the numerator is greater than or equal to the degree of the denominator, you must perform polynomial long division first. This will result in a polynomial plus a proper rational fraction. You then apply partial fraction decomposition only to the proper rational fraction part. The integral will be the integral of the polynomial plus the integral of the partial fractions.

