Introduction
In mathematics, various terms and operations form the foundation of more complex concepts and problem-solving techniques. One such term is “product.” In this blog post, we will explore what the product means in math, its applications, and some interesting nuances of multiplication across different mathematical fields. Whether you are a student starting your mathematical journey or someone revisiting concepts, this detailed guide will provide clarity and insights into the world of mathematical products.
Definition of product in math
So, what is “product” in math? In mathematics, product means the result you get after multiplying numbers together. The numbers that are being multiplied are known as factors. So, the final result is called the product when we multiply factors, whether they’re whole numbers, fractions, or even decimals. This concept is at the heart of many areas in mathematics, which is why it’s so important to understand the products definition.
Understanding the Basics of Product in Math
What Does Product Mean in Math?
The term “product” refers to the result of multiplying two or more numbers together. It is one of the four basic operations in arithmetic, alongside addition, subtraction, and division. When you multiply numbers, the result you obtain is called the product. For instance, if you multiply 2 by 3, the product is 6.
How to find the product in math
Figuring out the product in math is simple: you multiply the numbers. The process can vary from elementary multiplication problems, such as 2 x 3, to more complex ones involving bigger numbers or decimals. Regardless of the complexity, the answer derived from the multiplication operation is called a product – and yes, this holds even when variables are in the equation.
But what happens when there are more than two numbers or factors involved? Do not fret! The method remains the same when wondering, “what’s product in math?”.
Consider a simple example: To find the product of 2, 3, and 4, multiply them in any order. You can multiply 2 and 3 first to get 6, then multiply 6 by 4 to get 24. Alternatively, you can multiply 4 and 2 first to get 8, then multiply 8 by 3 to get 24. This flexibility is due to the commutative property of multiplication, which states that the order of numbers does not change the product.
It’s also important to remember that the math product of any number and zero is always zero. This is known as the zero property of multiplication.
When dealing with fractions or decimals, the process remains essentially the same. You multiply the fractions or the decimals directly. However, calculating these might require additional steps or a good grasp of fraction and decimal operations.
Lastly, multiplication and its product have a wide range of applications in real-world scenarios, from calculating the prices of multiple items to figuring out the area of a room. Therefore, understanding the concept of a product is not just crucial for math assignments but also practical in daily life.
The Significance of Multiplication and Products
Foundational Role in Arithmetic:
Multiplication, and by extension, products, play a crucial role in arithmetic. They are used not only in pure mathematics but also in everyday calculations such as calculating areas, understanding proportions, and converting measurements. Multiplication is a faster and more efficient method than repeated addition for combining multiple groups of the same size.
Applications of Product in Various Mathematical Disciplines
Algebra:
In algebra, the concept of the product extends beyond simple numbers to include variables, expressions, and polynomials. For example, when you multiply two binomials, such as (x + 2) and (x + 3), you use the FOIL method to find the product, which results in a quadratic polynomial.
Geometry:
In geometry, the product is used to calculate areas and volumes. The area of a rectangle, for example, is the product of its length and width. Similarly, the volume of a rectangular prism is the product of its length, width, and height.
Calculus:
In calculus, products are part of formulas for differentiation and integration, such as the product rule, which is used to differentiate functions that are products of other functions.
Real-World Examples Demonstrating the Use of Products
Business and Economics:
Products are integral to calculations related to finance and economics, such as computing interest, analyzing growth trends, and determining economic outputs. For instance, the Gross Domestic Product (GDP) of a country is the product of its total outputs of goods and services.
Science and Engineering:
In fields like physics and engineering, products are essential for formulas involving force, power, and energy calculations. For example, power is calculated as the product of voltage and current in electrical engineering.
Deep Dive: Special Types of Products in Mathematics
Dot Product and Cross Product in Vector Algebra:
In advanced mathematics, particularly in vector algebra, there are specialized types of products like the dot product and the cross product. The dot product of two vectors gives a scalar quantity that represents the magnitude in the direction of the first vector. The cross product, on the other hand, results in a vector that is perpendicular to both of the vectors being multiplied.
Matrix Multiplication:
Another complex form of multiplication is matrix multiplication, crucial in linear algebra. Unlike regular number multiplication, the product of two matrices is not commutative, meaning the order in which you multiply the matrices matters.
Teaching and Learning the Concept of Product
Visual Aids and Manipulatives:
Using visual aids like number lines, arrays, and area models can help students understand the concept of multiplication and products more clearly. These tools make abstract concepts tangible, especially for visual learners.
Interactive Learning:
Engaging students through interactive methods like games, digital apps, and puzzles that involve multiplication can make learning about products more enjoyable and memorable.
Commutative Property of Product
Interestingly, if the order of the multiplicand and multiplier are reversed, the product remains the same:
Let’s look at an example:
2 ✕ 3 = 6
Here, 2 is the multiplicand, 3 is the multiplier, and 6 is the product.
If we reverse the equation, we still get
3 ✕ 2 = 6
Fascinating, isn’t it?
Product of Fractions and Decimals
So far, we have learned how to calculate the product of whole numbers. Let’s now learn how to find the product of fractions and decimals!
Product of Fractions
Let’s learn this with the help of an example.
Suppose we have to find the product of the fractions 52 and 34.

Step 1: Multiply the numerator with the numerator and the denominator with the denominator.

Step 2: If you get an improper fraction, you can convert this into a mixed number.

We can also find the product of two mixed numbers or a fraction and a mixed number or even a whole number and a fraction by the same method by just ensuring that we convert our multiplicand and multipliers into fraction form first.
Product of Decimals
What makes a decimal number special?
The decimal point!
Multiplying two decimal numbers is the same as multiplying two whole numbers with the exception that we need to take care of the decimal point.
Let’s learn this with the help of an example.
Let’s multiply 1.5 and 1.2.
Step 1: Count the number of digits after the decimal point in both the numbers.
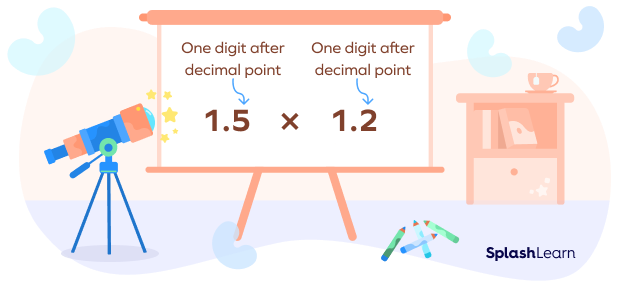
Step 2: So the total number of digits after the decimal point in our multiplication expression is 1 + 1 = 2.
Step 3: Multiply the two numbers without the decimal point.

Step 4: In this product, start from the right and place the decimal point, after the same number of places as the total number found in step 2. And that will be the answer to our decimal multiplication.

So the product of 1.5 and 1.2 will be 1.80.
