Mathematics is a vast field filled with numerous concepts and operations that form the foundation for various applications in science, engineering, economics, and everyday life. One such fundamental concept is the product. Whether you’re a student grappling with basic arithmetic or a professional delving into advanced mathematical theories, understanding what a product means in math is crucial. In this comprehensive guide, we’ll explore the definition, types, properties, and applications of the product in mathematics, ensuring you grasp its significance and utility.
Table of Contents
- What is a Product in Mathematics?
- Basic Multiplication: The Foundation of Product
- Properties of the Product
- Types of Products in Mathematics
- Applications of Products in Various Fields
- Common Mistakes and Misconceptions
- Conclusion
- Frequently Asked Questions (FAQs)
What is a Product in Mathematics?
In mathematics, the product refers to the result of multiplying two or more numbers, variables, or expressions together. It is one of the four elementary arithmetic operations, alongside addition, subtraction, and division. The concept of the product extends beyond simple numerical multiplication to more complex structures in algebra, geometry, and other branches of mathematics.
Example:
- Numerical Product: The product of 3 and 4 is 12, denoted as 3×4=12.
- Algebraic Product: The product of x and y is xy.
Understanding the product is essential as it forms the basis for more advanced mathematical operations and theories.
Basic Multiplication: The Foundation of Product
At its core, the product is synonymous with multiplication. Multiplication can be viewed as repeated addition. For instance, multiplying 4 by 3 (4×3) is equivalent to adding 4 three times: 4+4+4=12.
Multiplication Properties:
- Commutative Property: a×b=b×a
- Associative Property: (a×b)×c=a×(b×c)
- Distributive Property: a×(b+c)=(a×b)+(a×c)
These properties make multiplication a versatile and powerful tool in various mathematical operations.
Properties of the Product
Understanding the properties of the product helps in simplifying complex mathematical expressions and solving equations efficiently. Here are the key properties:
1. Commutative Property
The order in which two numbers are multiplied does not affect the product.
a×b=b×a
Example: 5×7=7×5=35
2. Associative Property
When multiplying three or more numbers, the way in which the numbers are grouped does not affect the product.
(a×b)×c=a×(b×c)
Example: (2×3)×4=2×(3×4)=24
3. Distributive Property
Multiplication distributes over addition and subtraction.
a×(b+c)=(a×b)+(a×c)
Example: 3×(4+5)=(3×4)+(3×5)=27
4. Identity Property
The product of any number and 1 is the number itself.
a×1=a
Example: 9×1=9
5. Zero Property
The product of any number and 0 is 0.
a×0=0
Example: 7×0=0
Types of Products in Mathematics
The concept of the product extends beyond simple multiplication. Different mathematical areas utilize various types of products to solve specific problems. Here are some notable types:
Scalar Product (Dot Product)
The dot product is an algebraic operation that takes two equal-length sequences of numbers (usually vectors) and returns a single number. It is widely used in physics and engineering to determine angles between vectors and projections.
Example:
For vectors A=[1,2,3] and B=[4,5,6],
A⋅B=(1×4)+(2×5)+(3×6)=32
Vector Product (Cross Product)
The cross product of two vectors in three-dimensional space results in a new vector that is perpendicular to the plane containing the original vectors. It is essential in physics for calculating torque and rotational forces.
Example:
For vectors A=[1,0,0] and B=[0,1,0],
A×B=[0,0,1]
Matrix Product
Matrix multiplication involves multiplying two matrices to produce a third matrix. It is fundamental in linear algebra, computer graphics, and solving systems of linear equations.
C=A×B
Example:
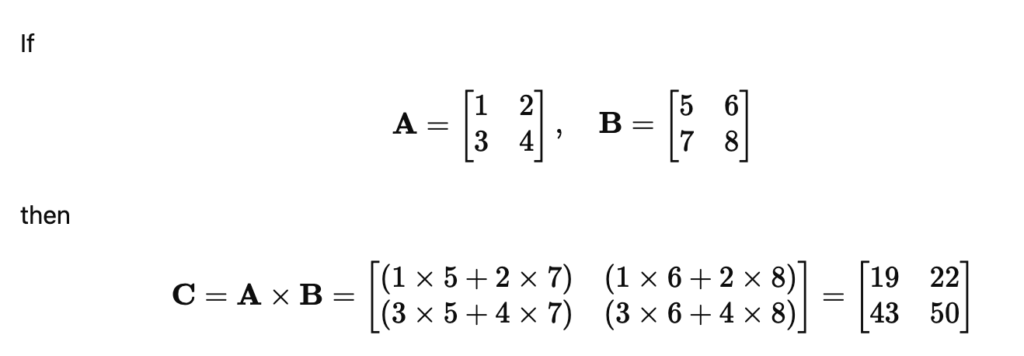
Polynomial Product
Multiplying polynomials involves applying the distributive property to expand the product into a new polynomial.
(2x+3)(x−4)=2x(x)+2x(−4)+3(x)+3(−4)=2x2−8x+3x−12=2x2−5x−12
Applications of Products in Various Fields
The concept of the product is ubiquitous across different disciplines. Here are some key applications:
1. Physics
Work Calculation: Work is the product of force and displacement.
Work=Force×DisplacementPower: Power is the rate at which work is done, often expressed as a product involving energy and time.
2. Engineering
Electrical Engineering: Ohm’s Law states that Voltage (V) is the product of current (I) and resistance (R).
V=I×RStructural Engineering: Calculations involving forces, moments, and stresses often utilize products of various quantities.
3. Economics
Total Cost: Total cost is the product of quantity and unit cost.
Total Cost=Quantity×Unit CostRevenue: Revenue is the product of price per unit and the number of units sold.
Revenue=Price×Quantity Sold
4. Computer Science
Algorithm Complexity: Understanding the product of operations helps in analyzing the time and space complexity of algorithms.
Graphics Rendering: Matrix products are fundamental in transforming and rendering images.
5. Biology and Medicine
Population Growth Models: Exponential growth models involve products of factors influencing population changes.
Dosage Calculations: Medical dosages often depend on products of weight and concentration.
Common Mistakes and Misconceptions
Grasping the concept of the product is essential, but students often encounter challenges and misconceptions. Here are some common pitfalls and how to avoid them:
1. Confusing Product with Sum
Mistake: Assuming the product of two numbers is the same as their sum.
Solution: Remember that the product involves multiplication, which generally results in larger values compared to addition.
2. Ignoring the Order in Non-Commutative Products
Mistake: Believing that all products are commutative, especially in matrix multiplication.
Solution: Understand that while scalar multiplication is commutative, matrix multiplication is not. Always maintain the correct order of matrices.
3. Misapplying the Distributive Property
Mistake: Incorrectly expanding products, especially with negative signs or exponents.
Solution: Carefully apply the distributive property step-by-step, paying attention to signs and exponents.
4. Overlooking Units in Applied Problems
Mistake: Ignoring the units when calculating products in real-world applications, leading to incorrect results.
Solution: Always include and convert units appropriately when performing multiplication in applied contexts.
Conclusion
The product is a fundamental concept in mathematics that extends far beyond simple multiplication. It plays a pivotal role in various branches of mathematics and has extensive applications across different fields such as physics, engineering, economics, and computer science. Understanding the product, its properties, and its various types empowers individuals to solve complex problems, analyze data effectively, and apply mathematical principles in real-world scenarios. Whether you’re a student building your mathematical foundation or a professional leveraging advanced mathematical tools, a solid grasp of the product is indispensable.
Frequently Asked Questions (FAQs)
1. What is the difference between scalar product and vector product?
The scalar product (dot product) results in a single number and measures the extent to which two vectors align. The vector product (cross product) results in a new vector perpendicular to the original vectors and measures the area spanned by them.
2. Is the product operation always commutative?
No. While scalar multiplication is commutative (a×b=b×a), some products like matrix multiplication are not commutative (AB=BA).
3. How is the product used in solving equations?
Products are used to simplify and solve equations by applying properties like the distributive, associative, and commutative properties. For example, factoring involves expressing a polynomial as a product of its factors.
4. Can the product of two negative numbers be negative?
No. The product of two negative numbers is positive. However, the product of a positive and a negative number is negative.
5. How does the concept of the product extend to higher mathematics?
In higher mathematics, products extend to complex structures like tensors, matrices, and functions. They are integral in fields like linear algebra, calculus, and abstract algebra.
