Volume Calculator
Use this volume calculator to easily calculate the volume of common bodies like a cube, rectangular box, cylinder, sphere, cone, and triangular prism. Volume formulas and explanations can be found below the tool.
(Here you could show an image or a schematic relevant to the chosen shape.)
How to calculate the volume of a body?
Depending on the particular body, there is a different formula and different required information you need to calculate its volume. Below are volume formulas for the most common types of geometric bodies – all of which are supported by our online volume calculator above. All measures need to be in the same unit. The result is always in cubic units: cubic centimeters, cubic inches, cubic meters, cubic feet, cubic yards, etc.
Volume calculations for three-dimensional objects are useful in a lot of sciences, in construction work and planning, in cargo shipping, in climate control (e.g. air conditioning calculations), swimming pool management, and more.
Volume of a cube
The volume formula for a cube is side3, as shown in the figure below:

The only information required to find the volume of a cube is the length of its side. Knowing that, take its cube and you have found the cube’s volume. It is the same as multiplying the area of one side by the depth of the cube. For this type of figure one barely needs a calculator to do the math.
Volume of a box
To find the volume of a rectangular box use the formula height x width x length, as seen in the figure below:

To calculate the volume of a box or rectangular tank you need three dimensions: width, length, and height. They are usually easy to measure due to the regularity of the shape, each side being a rectangle. By designating one dimension as the rectangular prism’s depth or height, the multiplication of the other two gives us the area which then needs to be multiplied by the depth / height to get the volume. To calculate the volume of a tank of a different shape, use our volume of a tank calculator.
Volume of a cylinder
The equation to find the volume of a cylinder is height x π x (diameter / 2)2, where (diameter / 2) is the radius of the base (d = 2 x r), so another way to write it is height x π x radius2. Essentially it consists of multiplying the area of the cylinder’s base by its height. The graph below illustrates the needed measurements:
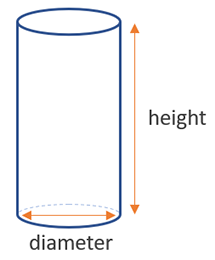
Two measurements are required at the minimum: the height of the cylinder and the diameter of its base. In many school formulas the radius is given instead, but in real-world situations it is much easier to measure the diameter instead of trying to pinpoint the midpoint of the circular base just so you can measure the radius. Our volume calculator requires that you insert the diameter of the base. Through the diameter the area of the cylinder base can be calculated and then the multiplication by its height results in its volume.
Volume of a sphere
To find the volume of a sphere, use the formula 4/3 x π x (diameter / 2)3, where (diameter / 2) is the radius of the sphere (d = 2 x r). Another way to write the equation is as 4/3 x π x radius3. A visual presentation can be seen in the figure below:

Same as with a circle, one only needs one measurement of the sphere to compute its volume: either its diameter or its radius.
Volume of a cone
The formula for a cone is (height x π x (diameter / 2)2) / 3, where (diameter / 2) is the radius of the base (d = 2 x r). The equation can also be expressed as (height x π x radius2) / 3, as seen in the figure below:

Despite being a somewhat complex shape, one only needs to know three dimensions to calculate the volume of a regular cone. For irregular cones, which are not supported by our tool, yet, you would also need to know the angle of the cone.
Volume of a triangular prism
The volume of a triangular prism is calculated using the formula (height x base x length) / 2. These length measurements can be seen in the figure below:

Similar to rectangular boxes, one needs just three dimensions: height, base, and length, in order to find a triangular prism’s volume.
Examples of volume formulae applications
Volume calculations have a vast array of practical applications. If you are faced with a construction project, home decoration DIY job, or certain engineering tasks, a volume calculator will help you if the figure you want to find the volume of falls within any of the above forms. Complex figures can usually be decomposed, at least approximately, to a sum of these basic figures.

