5.1. Indefinite integral
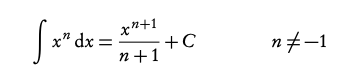
Integration with an internal function
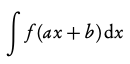
Integrate normally and multiply by 1/coefficient of x
Integration by substitution
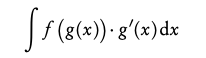
5.2. Definite integral
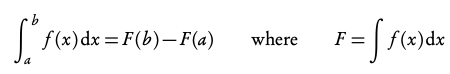
Be careful, the order you substitute a and b into the indefinite integral is relevant for your answer:
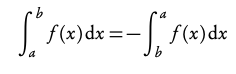
Area between a curve and the x-axis
By determining a definite integral for a function, you can find the area beneath the curve that is between the two x-values indicated as its limits.
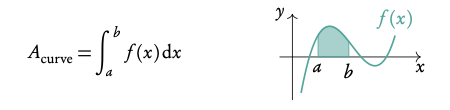
Note: the area below the x-axis gives a negative value for its area. You must take that value as a positive value to determine the area between a curve and the x-axis. Sketching the graph will show what part of the function lies below the x -axis.
Area between two curves
Using definite integrals you can also find the areas enclosed between curves.
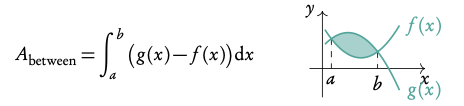
With g(x) as the “top” function (furthest from the x- axis). For the area between curves, it does not matter what is above/below the x-axis.
