Integration is essentially the opposite of derivation. The following equation shows how to integrate a function:
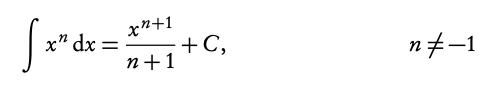
As you can see, every time you integrate the power on your variable will increase by 1 and you divide by the new power. This is opposite of what happens when you derive, then the power always decreases and you multiply by the original power.Whenever you integrate you also always add +C to this function. This accounts for any constant that may have been lost while deriving. As you may have noticed, whenever you do derivation any constants that were in the original function, f(x), become 0 in the derivative function, f′(x). In order to determine the value of C, you need to fill in a point that lies on the curve to set up an equation in which you can solve for C .
Note: This is the same thing you need to do when finding the y-intercept, C, for a linear function – see Functions: Linear functions.
Standard integration
Let f′(x) = 12x2 − 2
Given that f (−1) = 1, find f (x).
Separate summed parts (optional)
∫ 12x2 − 2dx = ∫ 12x2 dx + ∫ −2dx
2. Integrate
f(x) = ∫ 12x2 dx + ∫ −2dx=
12/3 x3 − 2x + C
3. Fill in values of x and f(x) to find C
Since f(−1) = 1,
4(−1)3 −2(−1) + C = 1
C = 3
So : f(x) = 4x3 − 2x + 3
5.1.1 Integration with an internal function
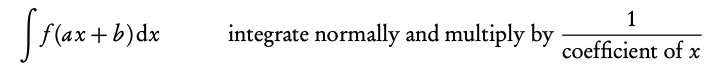
Example: Find the following integrals:
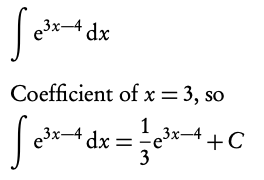
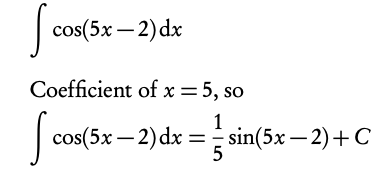
5.1.2 Integration by substitution
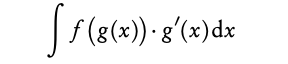
Usually these questions will be the most complicated-looking integrals you will have to solve. So if an integration question looks complicated, try to look for a function and its derivative inside the function you are looking to integrate; it is likely to be a question where you have to use the substitution method! Study the example to see how it’s done.
Integrate by substitution
Find ∫ 3x2 ex 3 dx
- Identify the inside function u, this is the function whose derivative is also inside f(x)
g(x) = u = x3
2. Find the derivative u′ = du/dx
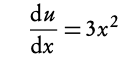
3. substitute u and du/dx into the integral (this way dx cancels out)
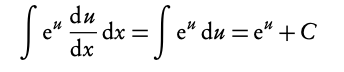
4. Substitute u back to get a function with x
∫ eu + C = ex3 + C
