If there are limit values indicated on your integral, you are looking to find a definite integral. This means that these values will be used to find a numeric answer rather than a function.
This is done in the following way, where the values for a and b are substituted as x-values into your indefinite integral:
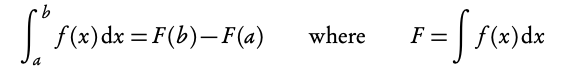
Be careful, the order you substitute a and b into the indefinite integral is relevant for your answer:
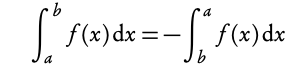
Solving definite integrals

- Find the indefinite integral (without +C)
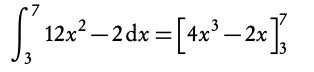
2. Fill in: F(b) − F(a)
(integral x = b) − (integral x = a)
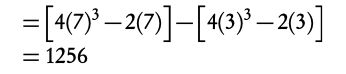
5.2.1 Area
Area between a curve and the x-axis
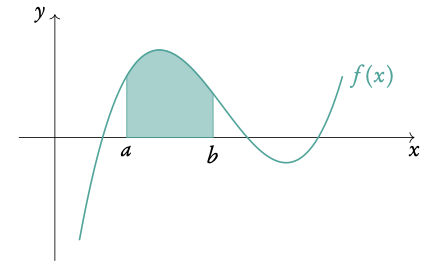
DB 5.5
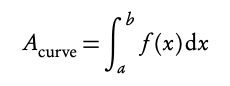
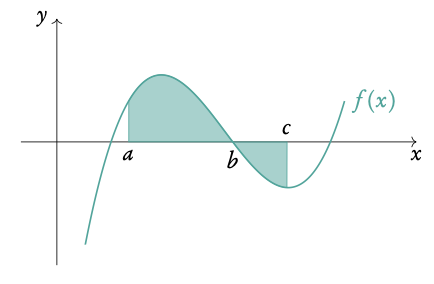
The area below the x-axis gives a negative value for its area. You must take that value as a positive value to determine the area between a curve and the x-axis. Sketching the graph will show what part of the function lies below the x-axis. So

Area between two curves
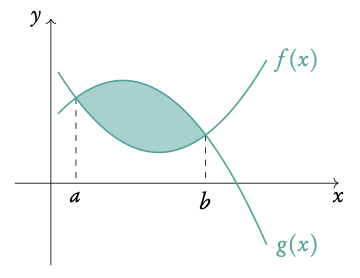
Using definite integrals you can also find the areas enclosed between curves:
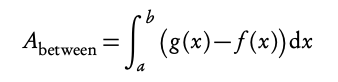
With g(x) as the “top” function (furthest from the x-axis). For the area between curves, it does not matter what is above/below the x-axis.
Finding areas with definite integrals.
Let y = x3 − 4x3 + 3x
Find the area from x = 0 to x = 3.
- Find the x-intercepts: f (x) = 0
x3 − 4x3 + 3x = 0, using the GDC: x = 0 or x = 1 or x = 3
2. If any of the x-intercepts lie within the range, sketch the function to see which parts lie above and below the x-axis.
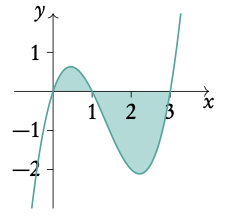
3. Setup integrals and integrate
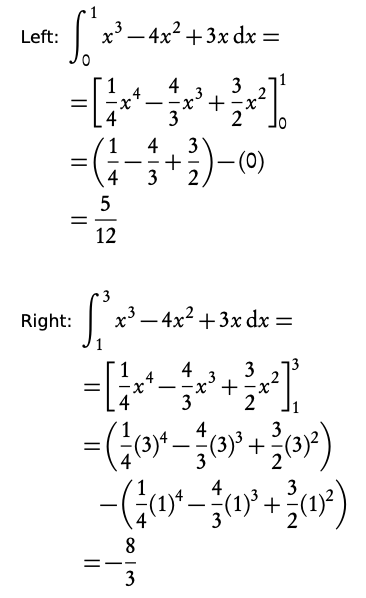
4. Add up the areas (and remember areas are never negative!)
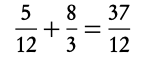
Alternatively, use the calculator to find areas
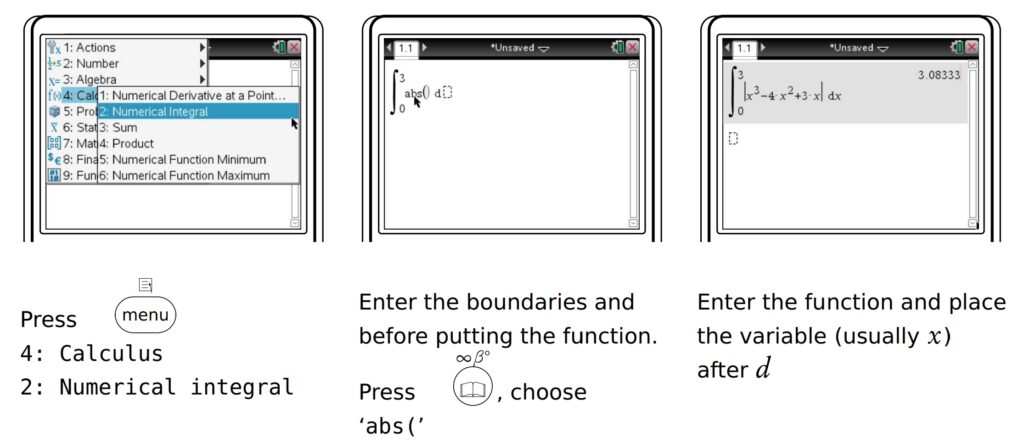
In this case, the area is 3.083
