Definitions
Sample space the list of all possible outcomes.
Event the outcomes that meet the requirement.
Probability for event A,

Dependent events two events are dependent if the outcome of event A affects the outcome of event B so that the probability is changed.
Independent events two events are independent if the fact that A occurs does not affect the probability of B occurring.
Conditional probability the probability of A, given that B has happened:

6.1. Single events

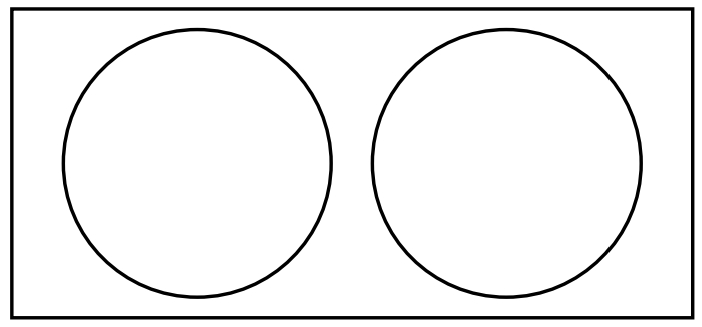
P(A∪B) = P(A) + P(B)
P(A∩B) = 0
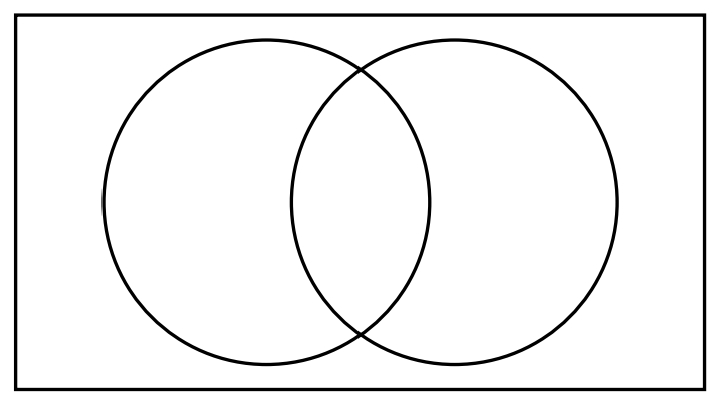
A∪B (union)

A∩B (intersect)
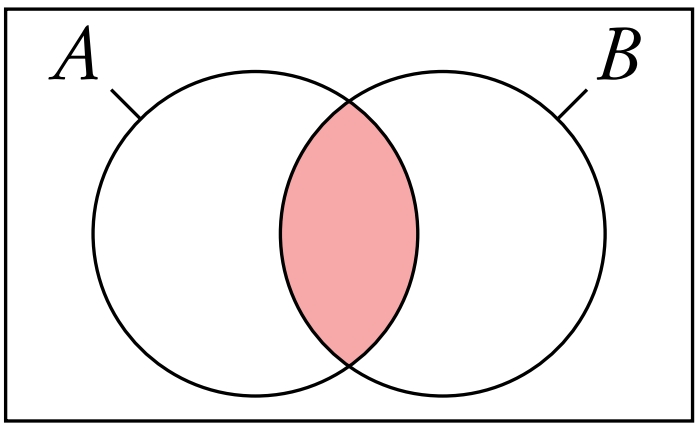
If independent: P(A∩B) = P(A) × P(B).
Compliment, A′ where P(A′) = 1 − P(A)
Exhaustive when everything in the sample space is contained in the events
6.2. Multiple events
Probabilities for successive events can be expressed through tree diagrams or a table of outcomes.
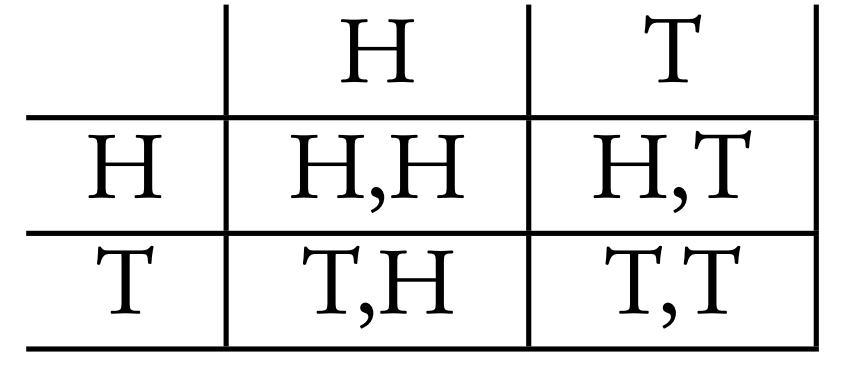
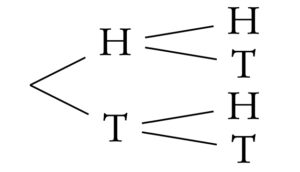
- one event and another, you multiply
- one event or another, you add
6.3. Distributions
For a distribution by function the domain of X must be defined as ∑P(X = x) = 1.
Expected value E(X) = ∑xP(X = x)
Binomial distribution X ∼ B(n, p) used in situations with only 2 possible outcomes and lots of trials
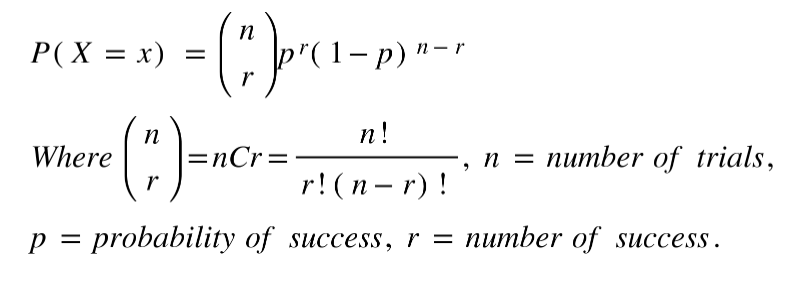
On calculator
- Binompdf(n,p,r) P(X = r)
- Binomcdf(n,p,r) P(x ≤ r)
Mean = np
Variance = npq
Normal distribution X ∼ N(μ, σ2)
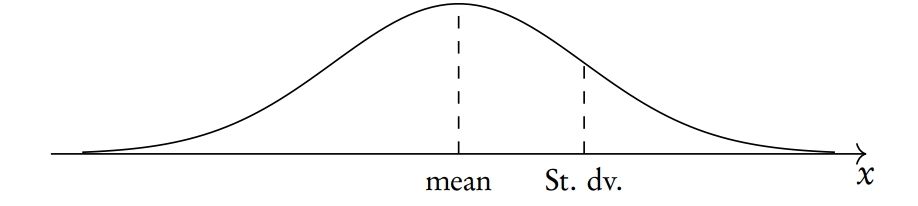
where μ = mean, σ = standard deviation
On calculator:
- normcdf(lowerbound, upperbound, = μ, σ)
- invnorm(area, = μ, σ)
