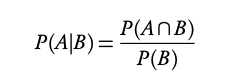Probability for single events can be visually expressed through Venn diagram
Sample space the list of all possible outcomes.
Event the outcomes that meet the requirement.
Probability for event A,
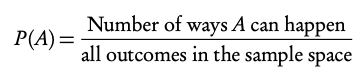
Here the shaded circle.

Note: These events are also exhaustive as there is nothing outside of the events (nothing in the sample space).
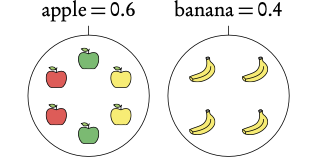
Example: What is the probability of picking each fruit?
Events do not overlap
P(A∪B) = P(A) + P(B)
P(A∩B) = 0

Combined events
Example: Of the apples 2 are red, 2 are green and 2 are yellow. What is the probability of picking a yellow apple?
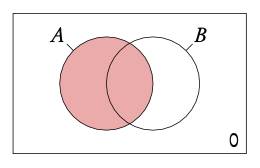
The intersect is the area the events overlap.
P(A∩B) = P(A) + P(B) − P(A∪B)
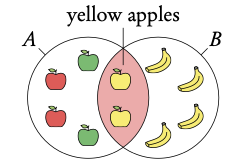

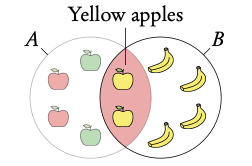
Example: What is the probability of picking an apple or a yellow fruit?
The union is the area contain by both events.
P(A∪B) = P(A) + P(B) − P(A∩B)
When an event is exhaustive the probability of the union is 1.

A: apples
B: yellow fruit
Event is exhaustive so probability of union is 1.
Compliment
Example: What is the probability of not picking a yellow fruit?
Everything that is not in the stated event.
P(A′) = 1 − P(A)
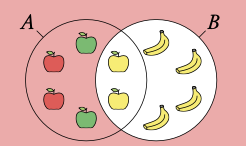
A: apples
B: yellow fruit
P(B′) = 1 − P(B) = 1 − 0.6 = 0.4
Conditional
Example: What is the probability of picking an apple given I pick a yellow fruit?
The probability given that some condition is already in place.