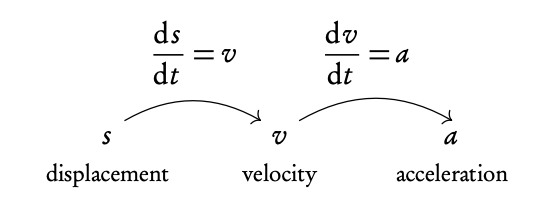Definitions
Differentiation is a way to find the gradient of a function at any point, written as f ′(x), y′ and dy/dx .
Tangent line to a point on a curve is a linear line with the same gradient as that point on the curve.
4.1. Polynomials
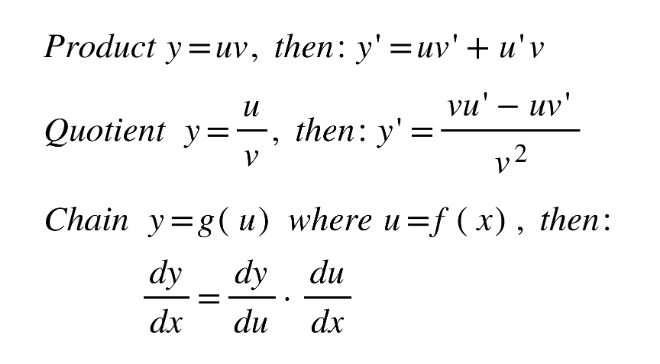
4.2. Tangent and normal
Tangent line with the same gradient as a point on a curve.
Normal perpendicular to the tangent m = −1/slope of tangent
Both are linear lines with general formula: y = mx + c .
1. Use derivative to find gradient of the tangent. For normal then do −1/slope of tangent .
2. Input the x-value of the point into f(x) to find y.
3. Input y, m and the x-value into y = mx + c to find c.
4.3. Turning points
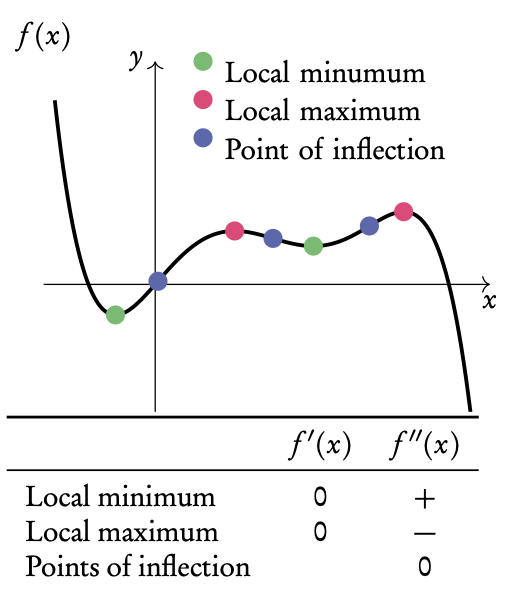
4.4. Sketching graphs
Gather information before sketching:
Intercepts
x-intercept: f (x) = 0
y-intercept: f (0)
Turning points
minima: f ′(x) = 0 and f ′′(x) < 0
maxima: f ′(x) = 0 and f ′′(x) > 0
point of inflection: f ′′(x) = 0
Asymptotes
vertical: x-value when the function divides by 0
horizontal: y-value when x → ∞
Plug the found x-values into f (x) to determine the y-values.
4.5. Applications
Kinematics
Derivative represents the rate of change, integration the reverse.