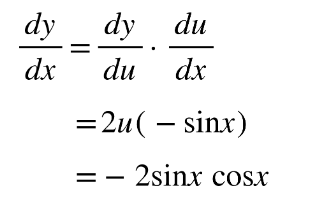As you have learnt in the section on functions, a straight line graph has a gradient. This gradient describes the rate at which the graph is changing and thanks to it we can tell how steep the line will be. In fact gradients can be found for any function – the special thing about linear functions is that their gradient is always the same (given by m in y = mx + c ). For polynomial functions the gradient is always changing. This is where calculus comes in handy; we can use differentiation to derive a function using which we can find the gradient for any value of x.
Using the following steps, you can find the derivative function (f ′(x)) for any polynomial function (f(x)).
Polynomial a mathematical expression or function that contains several terms often raised to different powers
e.g. y = 3x2, y = 121x5 + 7x3 + x or y = 4x⅔ + 2x⅓
Principles
y = f(x) = axn ⇒ dy/dx = f′(x) = naxn−1.
The (original) function is described by y or f(x), the derivative (gradient) function is described by dy/dx or f ′(x).
Derivative of a constant (number) 0
e.g. For f(x) = 5, f′(x) = 0
Derivative of a sum sum of derivatives.
If a function you are looking to differentiate is made up of several summed parts, find the derivatives for each part separately and then add them together again.
e.g. f(x) = axn and g(x) = bxm
f′( x ) + g′( x ) = naxn−1 + mbxm−1
4.1.1 Rules
With more complicated functions, in which several functions are being multiplied or divided by one another (rather than just added or subtracted), you will need to use the product or quotient rules.
Product rule
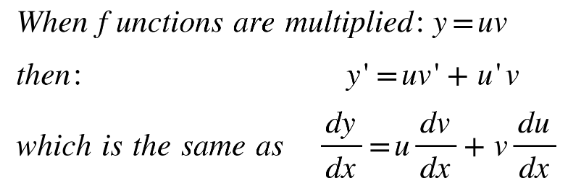
Example:
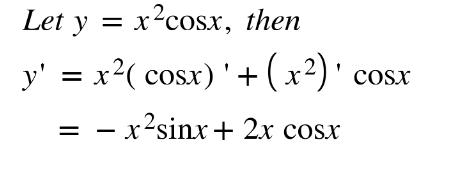
Quotient rule
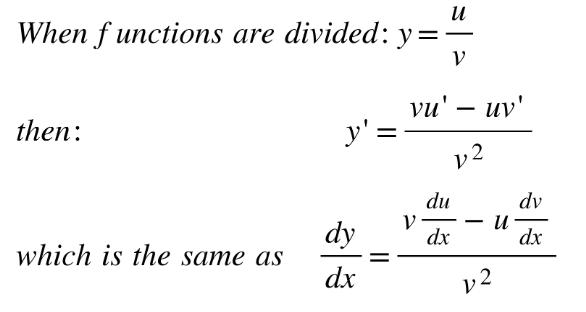
Example:
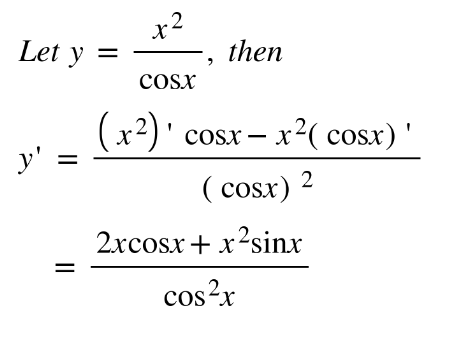
Chain Rule
When a function is inside another function: y = g(u) where u = f(x)
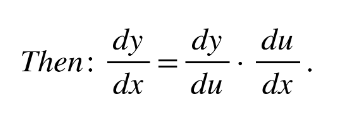
Note: A function inside another function is a composite function, f ◦ g(x), which we discussed in the Functions chapter
Differentiating with the chain rule
Determine what the inside (u) and outside (y) functions are
Inside function: u = cosx
Outside function: y = u2
2. Find u′ and y′
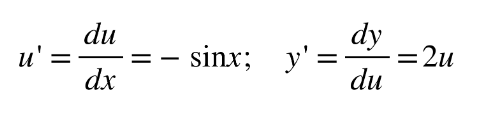
3. Fill in chain rule formula