Tangent a straight line that touches a curve at one single point. At that point, the gradient of the curve is equal to the gradient of the tangent.
Normal a straight line that is perpendicular to the tangent line:
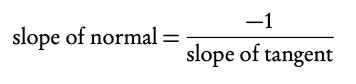
For any questions with tangent and/or normal lines, use the steps described in the following example.
Finding the linear function of the tangent.
- Find the derivative and fill in value of x to determine slope of tangent
f′(x) = 3x2
f′(2) = 3 · 22 = 12
2. Determine the y value
f(x) = 23 = 8
3. Plug the slope m and the y value in
y = mx + c
8 = 12x + c
4. Fill in the value for x to find c
8 = 12(2) + c ⇒ c =−16
eq. of tangent: y = 12x − 16
Note: Steps 1, 2 and 4 are identical for the equation of the tangent and normal
Finding the linear function of the normal.
Let f(x) = x3. Find the equation of the normal at x = 2
- Find the derivative and fill in value of x to determine slope of tangent
f ′(2) = 12
2. Determine the y value
f(x) = 8
3. Determine the slope of the normal
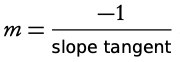
and plug it and the y-value into y = mx + c
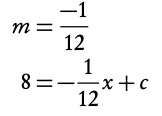
4. Fill in the value for x to find c
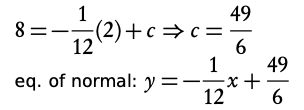
Note: Steps 1, 2 and 4 are identical for the equation of the tangent and normal
To find the gradient of a function for any value of x.
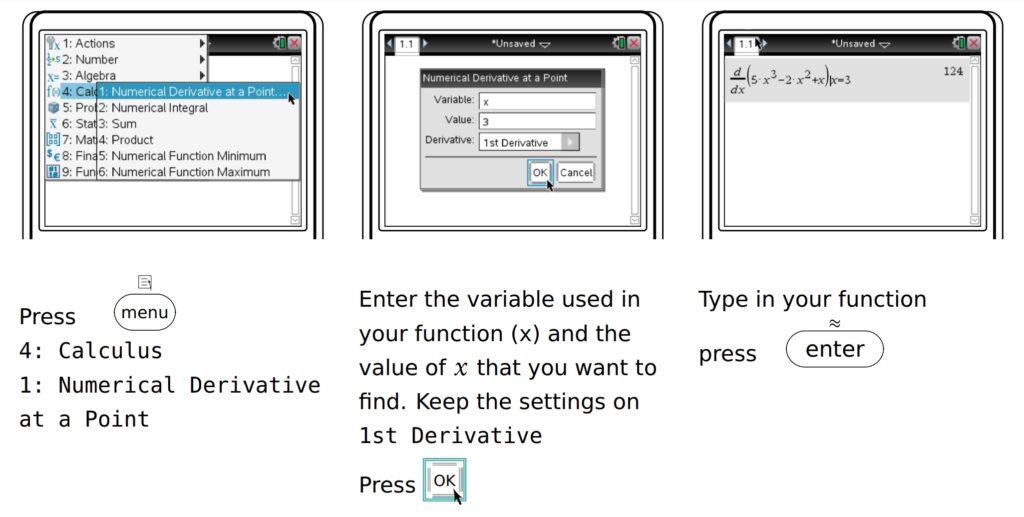
In this case, f′(3) = 124
