There are three types of turning points:
- Local maxima
- Local minima
- Points of inflection
We know that when f′(x) = 0 there will be a maximum or a minimum. Whether it is a maximum or minimum should be evident from looking at the graph of the original function. If a graph is not available, we can find out by plugging in a slightly smaller and slightly larger value than the point in question into f′(x). If the smaller value is negative and the larger value positive then it is a local minimum. If the smaller value is positive and the larger value negative then it is a local maximum.
If you take the derivative of a derivative function (one you have already derived) you get the second derivative. In mathematical notation, the second derivative is written as
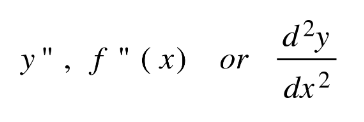
We can use this to determine whether a point on a graph is a maximum, a minimum or a point of inflection as demonstrated in the following Figure 4.1.
Figure 4.1: Graph that shows a local maximum, a local minimum and points of inflection
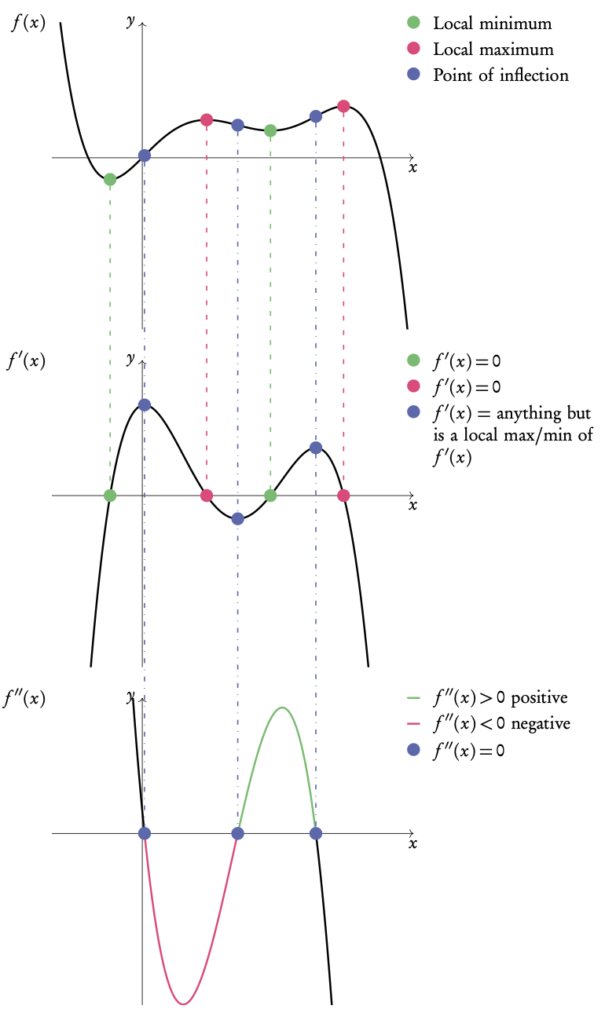
Note: Notice how the points of inflection of f (x) are minima and maxima in f ′(x) and thus equal 0 in f ′′(x)
Finding turning points
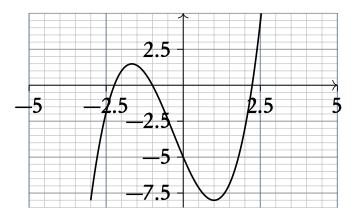
The function f(x) = x3 + x2 − 5x − 5 is shown. Use the first and second derivative to find its turning points: the minima, maxima and points of inflection (POI).
1. Find the first and second derivative
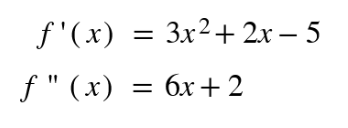
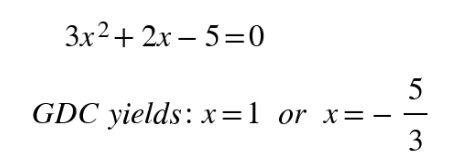
3. Find y-coordinates by inserting the x-value(s) into the original f (x)
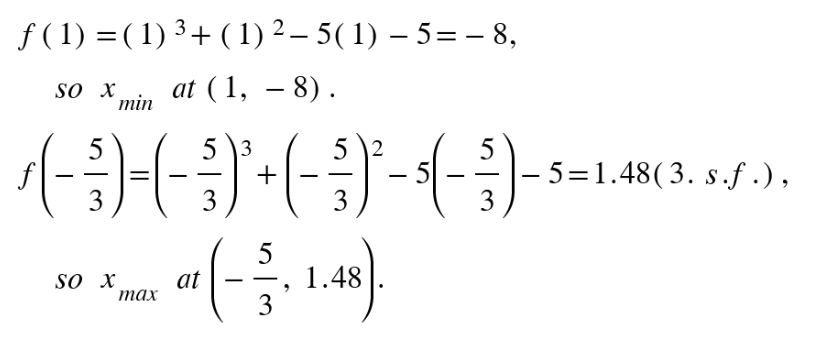
4. Find POI by setting f ′′(x) = 0
6x + 2 = 0
5. Enter x-values into original function to find coordinates
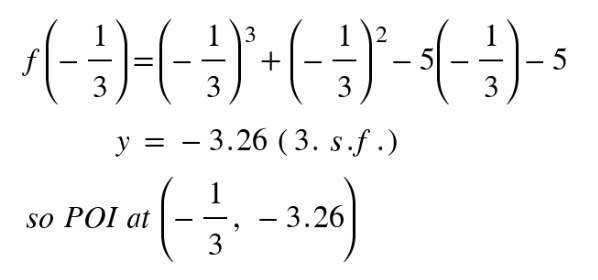
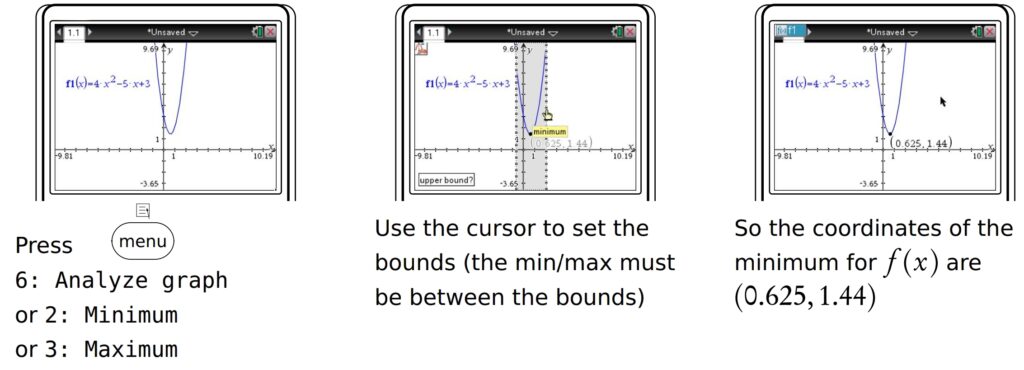
Finding turning points (local maximum/minimum) of a function using GDC
Find the coordinates of the local minimum for f (x) = 4x2 − 5x + 3