📐 Complete Algebra Cheat Sheet
Table of Contents & Formula Reference Guide
For IB, AP, GCSE, IGCSE & More
📚 Table of Contents
🎯 Why This Algebra Cheat Sheet Matters
Algebra forms the foundation of advanced mathematics across all major curricula including IB (International Baccalaureate), AP (Advanced Placement), GCSE, IGCSE, A-Levels, and SAT preparation. This comprehensive formula sheet consolidates essential algebraic concepts, providing students with quick access to critical formulas during revision and problem-solving sessions.
- Universal Application: These formulas apply across multiple examination boards and curricula
- Exam Essential: Core formulas frequently tested in standardized assessments
- Time-Saving: Quick reference guide reduces formula lookup time during practice
- Comprehensive Coverage: From basic sequences to advanced binomial expansion
1️⃣ Sequences
Arithmetic Sequences
An arithmetic sequence has a constant difference between consecutive terms.
Geometric Sequences
A geometric sequence has a constant ratio between consecutive terms.
Sigma Notation
A shorthand notation to show the sum of a number of terms in a sequence.
2️⃣ Exponents & Powers
Basic Exponent Laws
Negative & Fractional Exponents
Advanced Exponent Rules
3️⃣ Logarithms & Laws
Basic Logarithm Definitions
Laws of Logarithms
Special Logarithms
4️⃣ Binomial Expansion
Binomial Theorem
In an expansion of a binomial in the form (a + b)n, each term can be described as nCr·an-r·br, where nCr is the coefficient.
Binomial Coefficient
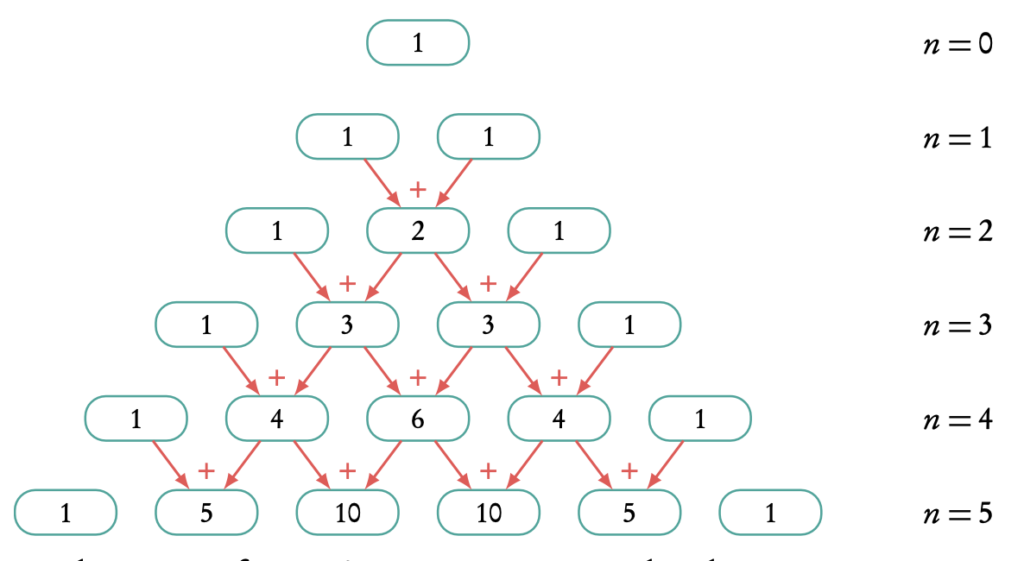
Pascal's Triangle Method
Find the coefficient using Pascal's Triangle:
Common Binomial Expansions
5️⃣ Quadratic Formulas
Standard Form & Quadratic Formula
For a quadratic equation in standard form:
Discriminant
Vertex Form
Completing the Square
To convert from standard form to vertex form:
Sum and Product of Roots
6️⃣ Polynomial Identities
Difference & Sum of Squares
Cubic Identities
Three-Term Expansions
Fourth Power Identities
7️⃣ Linear Equations & Functions
Slope (Gradient)
Equation Forms
Parallel & Perpendicular Lines
Distance & Midpoint
8️⃣ Inequalities
Inequality Rules
Basic properties of inequalities:
Absolute Value Inequalities
📖 Study Tips for Mastering Algebra
- Practice Regularly: Algebra skills improve with consistent practice. Work through varied problems daily rather than cramming.
- Understand, Don't Memorize: Focus on understanding why formulas work rather than just memorizing them.
- Check Your Work: Always substitute solutions back into original equations to verify correctness.
- Work Backwards: When stuck, try working from the answer choices backward (especially useful in multiple-choice exams).
- Identify Patterns: Recognize common algebraic patterns like difference of squares, perfect square trinomials, and factoring techniques.
- Use Multiple Methods: Learn different approaches to solving problems (graphing, algebraic, numeric) to deepen understanding.
- Master the Basics First: Ensure strong fundamentals in order of operations, fraction operations, and basic equation solving before advancing.
🎓 Common Algebra Applications Across Curricula
- IB Mathematics: Algebra forms the foundation for Analysis & Approaches (AA) and Applications & Interpretation (AI) courses, appearing in Paper 1 and Paper 2 assessments.
- AP Calculus: Strong algebraic manipulation skills are essential for differentiation, integration, and solving calculus problems efficiently.
- GCSE/IGCSE: Algebra comprises approximately 30% of exam content, including solving equations, rearranging formulas, and graph work.
- A-Level Mathematics: Advanced algebra including partial fractions, mathematical induction, and complex algebraic manipulation.
- SAT/ACT: Approximately 35-40% of math questions involve algebraic reasoning and equation-solving.
👨🏫 About the Author
Adam
Co-Founder @ RevisionTown
Math Expert in Various Curricula: IB, AP, GCSE, IGCSE, A-Levels
Dedicated to helping students master mathematics through comprehensive resources, clear explanations, and targeted exam preparation materials.
💪 Master these formulas through practice and understanding!
Visit RevisionTown.com for more comprehensive study materials
1.1 Sequences
Arithmetic: +/− common difference
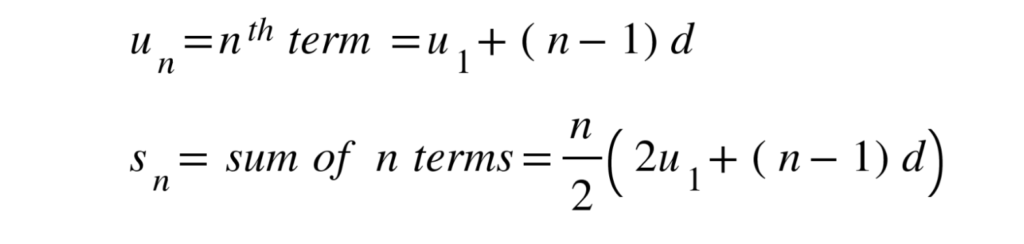
with u1 = a = 1st term, d = common difference.
Geometric: ×/÷ common ratio
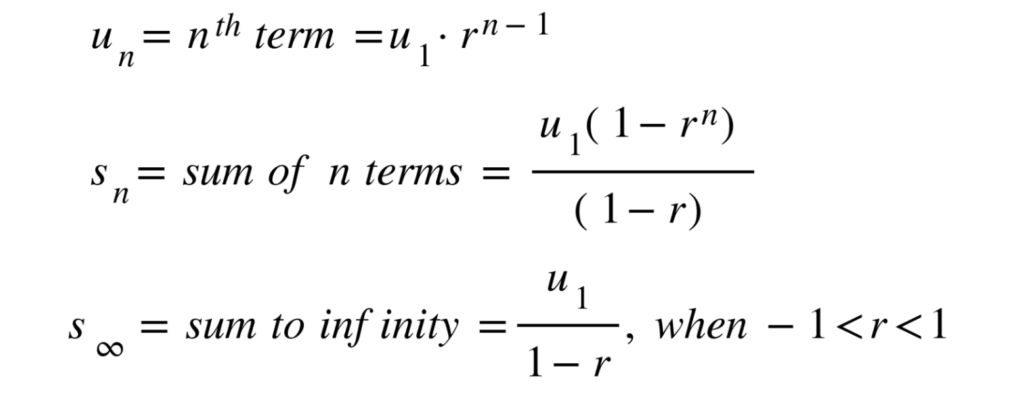
with u1 = a = 1st term, r = common ratio.
Sigma notation
A shorthand to show the sum of a number of terms in a sequence.
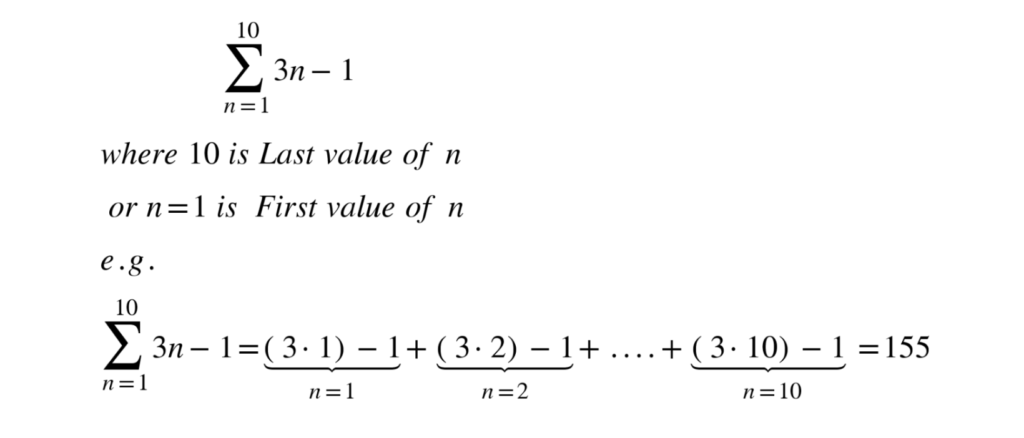
1.2 Exponents and logarithms
Exponents
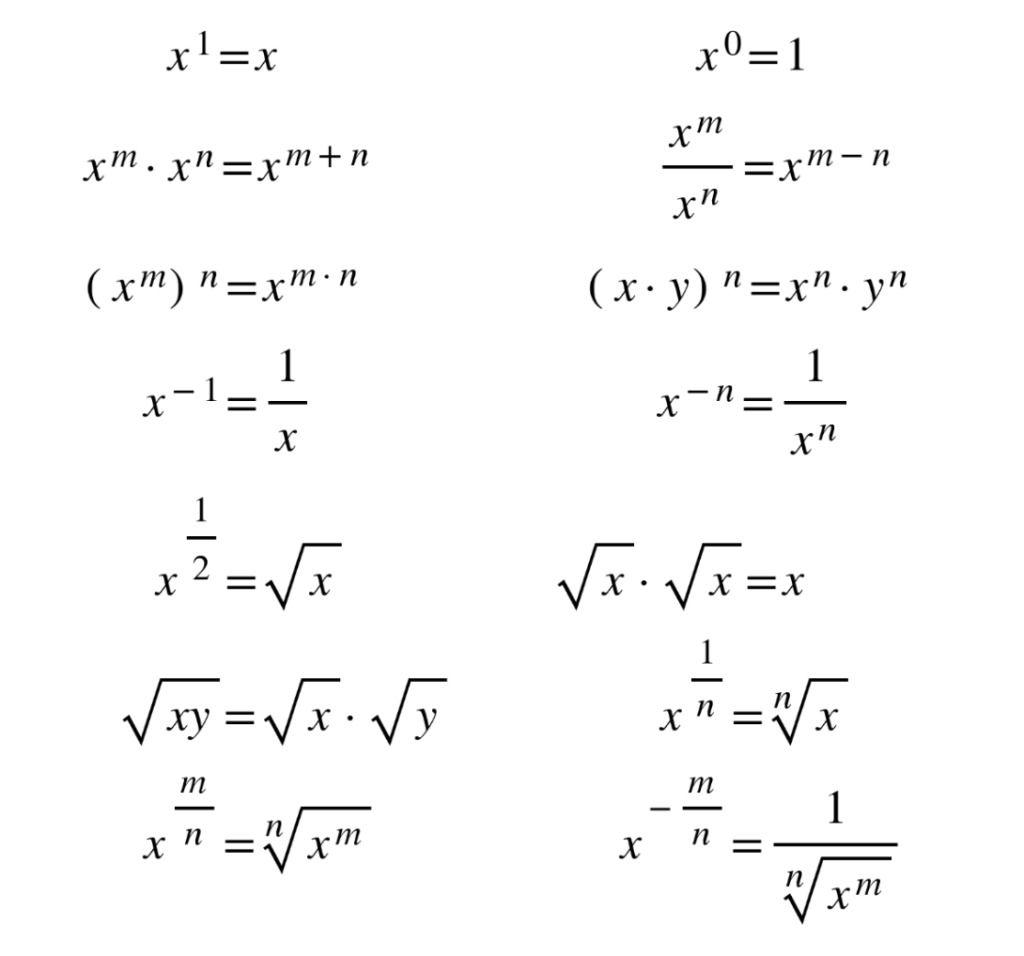
Logarithms
loga ax = x
aloga b = b
Let ax = b, isolate x from the exponent: loga ax = x = loga b
Let loga x = b, isolate x from the logarithm: aloga x = x = ab
Laws of logarithms
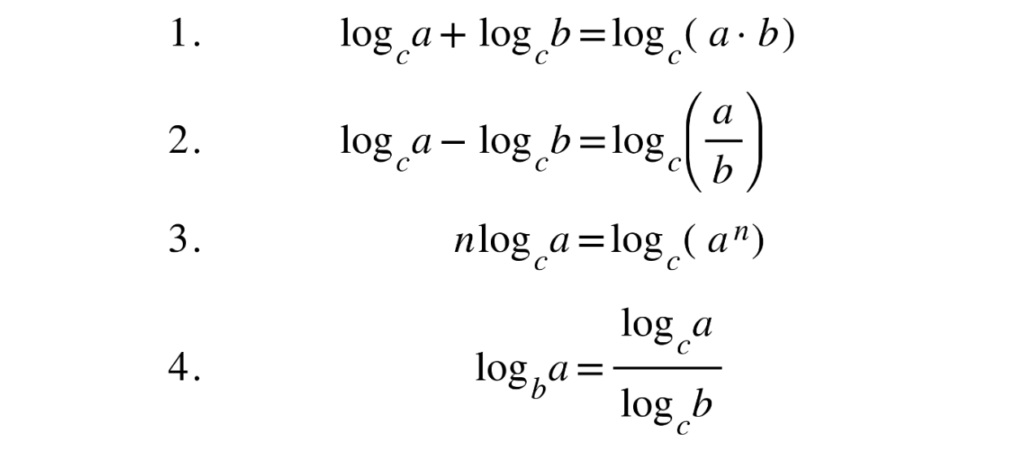
1.3. Binomial Expansion
In an expansion of a binomial in the form (a + b)n . Each term can be described as nCran−rbr, where nCr is the coefficient.
The full expansion can be written thus
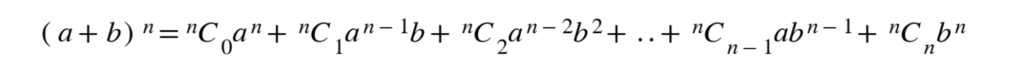
Find the coefficient using either pascals triangle
Or the nCr function on your calculator
