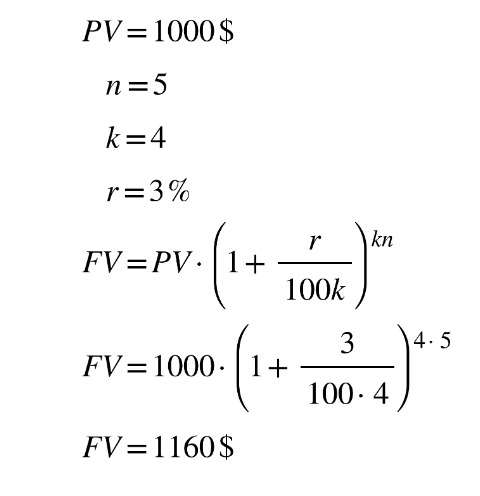Number and algebra study guide
Sequences: Complete Study Notes and Formulae
Sequences are one of the most useful pattern topics in school mathematics because they connect number sense, algebra, functions, recursion, finance, growth models, and series. This guide explains the core sequence types, the formulas you need, how to recognize each pattern, and how to solve exam-style questions without turning every problem into guesswork.
What Is a Sequence?
A sequence is an ordered list of terms. The terms might be numbers, algebraic expressions, shapes, or values generated by a rule, but the order matters. In the sequence \(2, 5, 8, 11, 14\), the first term is \(2\), the second term is \(5\), the third term is \(8\), and so on. If you rearrange those values, you no longer have the same sequence because each term is tied to its position.
The central question in most sequence problems is simple: what rule connects the position of a term to its value? Sometimes the rule is obvious from the differences between terms. Sometimes it is easier to look at ratios. Sometimes the rule depends on earlier terms rather than directly on \(n\), the position number. Once you can identify the structure, you can predict later terms, find missing values, calculate totals, and model real situations.
For students, sequences act as a bridge between arithmetic and algebra. Early sequence questions may ask you to continue a pattern. Later questions may ask for an explicit formula, a recursive definition, a sum of terms, or the limiting behavior as \(n\) becomes large. That progression is why sequences appear across many courses: they are simple enough to begin with pattern recognition, yet powerful enough to support calculus, statistics, computing, and financial mathematics.
Some sequences are finite, meaning they stop after a fixed number of terms. For example, the marks from six tests form a finite sequence. Other sequences are infinite, meaning the pattern continues without a final term. The counting numbers \(1, 2, 3, 4, \ldots\) form an infinite sequence. In exam questions, finite sequences often connect to totals or practical constraints, while infinite sequences often connect to limits, convergence, and series.
If you are using this page alongside broader algebra revision, it pairs naturally with RevisionTown's complete algebra cheat sheet and the number and algebra formulae for AA SL and AA HL. Those pages give the wider algebra toolkit that makes sequence formulas easier to manipulate.
Sequence Notation and Vocabulary
Sequence notation looks compact, but each symbol has a practical job. The expression \(a_n\) means the term in position \(n\). The value of \(n\) is usually a positive integer: \(1, 2, 3, 4, \ldots\). So \(a_1\) is the first term, \(a_2\) is the second term, and \(a_{20}\) is the twentieth term. Some courses use \(u_n\) instead of \(a_n\), but the meaning is the same.
The first term is commonly written as \(a_1\). Some advanced contexts start sequences at \(a_0\), especially in computing, power series, or recurrence relations. You must check the starting index before using a formula because the same pattern can have different formulas depending on whether the first listed term is called \(a_0\) or \(a_1\). This is one of the most common sources of off-by-one errors.
| Notation | Meaning | Example |
|---|---|---|
| \(a_n\) | The term in position \(n\) | If \(a_n = 3n + 1\), then \(a_5 = 16\) |
| \(a_1\) | The first term when indexing starts at \(1\) | For \(4, 7, 10, \ldots\), \(a_1 = 4\) |
| \(d\) | Common difference in an arithmetic sequence | For \(4, 7, 10, \ldots\), \(d = 3\) |
| \(r\) | Common ratio in a geometric sequence | For \(3, 6, 12, \ldots\), \(r = 2\) |
| \(S_n\) | Sum of the first \(n\) terms | \(S_5\) means \(a_1 + a_2 + a_3 + a_4 + a_5\) |
Explicit and Recursive Rules
An explicit rule gives \(a_n\) directly in terms of \(n\). For example, \(a_n = 5n - 2\) lets you calculate \(a_{50}\) by substituting \(n = 50\). You do not need \(a_{49}\). Explicit formulas are efficient, especially when you need a term far along in the sequence.
A recursive rule defines a term using one or more previous terms. For example, \(a_1 = 3\) and \(a_n = a_{n-1} + 4\) tells you to start at \(3\) and add \(4\) each time. Recursive formulas are natural when a process grows step by step, but they require a starting value. Without the starting value, the rule \(a_n = a_{n-1} + 4\) describes many possible sequences.
Both forms can describe the same sequence. A strong student should be able to move between them for arithmetic and geometric patterns. That skill matters in exam questions that say "write a recursive definition" after you have already found the nth term, or questions that give a recurrence and ask for a direct formula.
Arithmetic Sequences
An arithmetic sequence has a constant difference between consecutive terms. If you subtract any term from the next term, you get the same value every time. The sequence \(7, 11, 15, 19, 23, \ldots\) is arithmetic because each term increases by \(4\). The common difference is \(d = 4\).
Arithmetic sequences model situations with equal additive change: a taxi fare that increases by a fixed amount per kilometer, a savings plan where the same amount is added each week, a staircase pattern that adds the same number of blocks at each stage, or a linear function evaluated at equally spaced input values. Algebraically, arithmetic sequences are the discrete version of straight lines.
Here \(a_1\) is the first term, \(d\) is the common difference, and \(n\) is the term position.
The formula works because moving from the first term to the \(n\)-th term requires \(n - 1\) jumps. To reach the second term, you add one \(d\). To reach the third term, you add two copies of \(d\). To reach the tenth term, you add nine copies of \(d\). That is why the multiplier is \(n - 1\), not \(n\).
Find \(a_n\) for \(6, 13, 20, 27, \ldots\).
The first term is \(a_1 = 6\). The common difference is \(d = 13 - 6 = 7\). Substitute into the formula:
\[ a_n = 6 + (n - 1)7 = 6 + 7n - 7 = 7n - 1 \]So the explicit rule is \(a_n = 7n - 1\).
Arithmetic Sequence Sum
The sum of the first \(n\) terms of an arithmetic sequence is written as \(S_n\). There are two common versions of the formula. Use the first version when you know the first and last terms. Use the second version when you know the first term and common difference.
The first formula is based on the average of the first and last terms. In an arithmetic sequence, pairs from opposite ends have the same sum. For example, in \(2, 5, 8, 11, 14\), the first and last add to \(16\), the second and second-last also add to \(16\), and the middle term is half of \(16\). The total is the number of terms multiplied by the average term.
For more practice with this specific pattern, use the arithmetic sequence calculator and the detailed arithmetic sequence complete guide. They are useful when you want to check values quickly while still understanding the formula behind the result.
Geometric Sequences
A geometric sequence has a constant ratio between consecutive nonzero terms. Instead of adding the same amount each time, you multiply by the same amount. The sequence \(5, 15, 45, 135, \ldots\) is geometric because each term is multiplied by \(3\). The common ratio is \(r = 3\).
Geometric sequences are common in growth and decay problems. Compound interest, population growth, radioactive decay, depreciation, repeated percentage change, bouncing heights, and scale factors all use multiplicative change. When a quantity changes by a fixed percentage over equal time periods, the model is usually geometric rather than arithmetic.
Here \(a_1\) is the first term, \(r\) is the common ratio, and \(n\) is the term position.
The exponent is \(n - 1\) for the same structural reason as the arithmetic formula. To reach the first term, you have used zero multiplications by \(r\). To reach the second term, you multiply once. To reach the third term, you multiply twice. Therefore the \(n\)-th term uses \(n - 1\) copies of \(r\).
Find the explicit formula for \(2, 10, 50, 250, \ldots\).
The first term is \(a_1 = 2\). The common ratio is \(r = 10 / 2 = 5\). Therefore:
\[ a_n = 2(5)^{n - 1} \]To find \(a_6\), calculate \(2(5)^5 = 6250\).
Geometric Sequence Sum
The sum of a finite geometric sequence has a different formula from an arithmetic sum because the terms are multiplied by a constant ratio. If \(r \ne 1\), the sum of the first \(n\) terms is:
An equivalent version is \(S_n = \frac{a_1(r^n - 1)}{r - 1}\). Both give the same result when used correctly.
If \(r = 1\), every term is the same, so the sum is simply \(S_n = na_1\). That special case is easy to miss because the standard fraction formula has a denominator of zero when \(r = 1\).
Infinite Geometric Series
An infinite geometric series can have a finite sum if the terms become smaller fast enough. This happens when the absolute value of the common ratio is less than \(1\):
If \(r = \frac{1}{2}\), the terms halve each time and approach zero. If \(r = -\frac{1}{2}\), the terms alternate signs while still shrinking toward zero. If \(r = 2\), the terms grow without bound, so there is no finite infinite sum. This distinction is central when sequence work develops into series work, especially in calculus. For a deeper follow-up, see RevisionTown's pages on sequences and series, convergence of power series, and alternating series and error bounds.
Quadratic Sequences
A quadratic sequence has constant second differences. That means the first differences are not constant, but the differences between those first differences are constant. The sequence \(4, 9, 16, 25, 36, \ldots\) is quadratic because it is generated by \(a_n = (n + 1)^2\), and its first differences are \(5, 7, 9, 11, \ldots\). The second differences are \(2, 2, 2, \ldots\).
Quadratic sequences are connected to parabolas. If you plot the term position \(n\) on the horizontal axis and the term value \(a_n\) on the vertical axis, the points lie on a quadratic curve. This is why a quadratic sequence has a rule of the form:
The letters \(A\), \(B\), and \(C\) are constants. This guide uses capital letters here to avoid confusion with \(a_n\), the term notation. In many textbooks, the same formula is written as \(an^2 + bn + c\).
Finding a Quadratic nth Term
The cleanest method is to use differences. If the second difference is constant and equal to \(2A\), then \(A\) is half of the second difference. After that, subtract \(An^2\) from the original sequence to leave a linear sequence. Then find the linear part \(Bn + C\).
Find the nth term of \(5, 12, 23, 38, 57, \ldots\).
First differences: \(7, 11, 15, 19, \ldots\).
Second differences: \(4, 4, 4, \ldots\).
Since \(2A = 4\), we have \(A = 2\). Now compare the sequence with \(2n^2\):
| \(n\) | Original \(a_n\) | \(2n^2\) | Difference |
|---|---|---|---|
| 1 | 5 | 2 | 3 |
| 2 | 12 | 8 | 4 |
| 3 | 23 | 18 | 5 |
| 4 | 38 | 32 | 6 |
The remaining sequence is \(3, 4, 5, 6, \ldots\), which has rule \(n + 2\). Therefore:
\[ a_n = 2n^2 + n + 2 \]Quadratic sequences reward organized working. Lay out the terms, first differences, and second differences in rows. Do not try to jump straight to the formula unless the pattern is obvious. In exams, a clear difference table can earn method marks even if an arithmetic slip appears later.
Recursive Sequences
A recursive sequence defines each term using one or more earlier terms. The rule needs at least one initial condition, also called a starting value or base case. For example, \(a_1 = 4\), \(a_n = a_{n-1} + 6\) is recursive. It says the first term is \(4\), and each new term is \(6\) more than the previous term.
Recursive notation is especially useful when a process is naturally step based. A bank balance after monthly interest depends on the previous balance. The number of bacteria after one hour depends on the number from the previous hour. A computer algorithm may build each output from earlier outputs. In those situations, the recurrence describes the process more directly than a closed formula.
The biggest weakness of recursion is that it can be slow for finding distant terms. If you want \(a_{100}\), a recursive rule may require many steps. An explicit rule gives the answer in one substitution. However, recursion often gives better insight into how the sequence is generated, which is why both forms are important.
Fibonacci as a Recursive Pattern
The Fibonacci sequence is the classic example of a recursive sequence that depends on two previous terms:
The terms begin \(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \ldots\). Each term after the first two is the sum of the two terms before it. Fibonacci numbers also connect to the golden ratio, usually written as \(\phi\). If you are studying that connection, RevisionTown's golden ratio and Fibonacci formula guide gives a focused explanation.
When Recursive Definitions Need Care
Always check how many previous terms the recurrence uses. If a rule uses only \(a_{n-1}\), one starting value is usually enough. If it uses \(a_{n-1}\) and \(a_{n-2}\), two starting values are required. If it uses \(a_{n-3}\), three starting values may be needed. A recurrence without enough initial information is incomplete.
Special Sequence Families
Beyond arithmetic, geometric, quadratic, and recursive sequences, several named sequence families appear often in school mathematics. You do not need to memorize every possible sequence, but recognizing common families helps you see structure quickly.
Triangular Numbers
Triangular numbers count dots that can be arranged into equilateral triangular patterns. The first triangular number is \(1\), the second is \(3\), the third is \(6\), and the fourth is \(10\). Each new term adds the next counting number. This gives a direct link between triangular numbers and arithmetic series:
This formula appears in many disguise problems. If a theater has one seat in the first row, two seats in the second row, three in the third row, and so on, the total number of seats after \(n\) rows is triangular. If a tournament counts handshakes or pairings, triangular-number reasoning often appears.
Square and Cube Numbers
Square numbers and cube numbers are generated by powers. Square numbers come from \(n^2\), while cube numbers come from \(n^3\). Their differences reveal their degree. Square numbers have constant second differences, so they are quadratic. Cube numbers have constant third differences, so they are cubic. This idea generalizes: a polynomial sequence of degree \(k\) has constant \(k\)-th differences.
Harmonic Sequences
A harmonic sequence is formed from reciprocals of an arithmetic sequence. For example, \(1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots\) is harmonic because the reciprocals are \(1, 2, 3, 4, \ldots\), which form an arithmetic sequence. Harmonic patterns become important in calculus and series, especially when comparing convergence behavior.
Alternating Sequences
An alternating sequence changes sign repeatedly, such as \(3, -6, 12, -24, 48, \ldots\). This can happen when the common ratio is negative. If \(r = -2\), each term changes sign and doubles in magnitude. If \(r = -\frac{1}{2}\), each term changes sign but shrinks in magnitude. That distinction matters when deciding whether an infinite series can converge.
Sigma Notation and the Link to Series
A sequence lists terms. A series adds terms. Sigma notation is the compact way to write a sum of many terms. The Greek capital sigma symbol is written in MathJax as \(\sum\). A typical expression looks like this:
This means "add the terms \(a_k\) as \(k\) goes from \(1\) to \(n\)." The letter \(k\) is an index variable. It changes through the listed integer values, and the expression beside the sigma tells you what to add each time.
Substitute \(k = 1, 2, 3, 4, 5\):
\[ (2(1) + 1) + (2(2) + 1) + (2(3) + 1) + (2(4) + 1) + (2(5) + 1) \] \[ 3 + 5 + 7 + 9 + 11 = 35 \]Sigma notation is not a new type of mathematics; it is a compressed way of writing repeated addition. Once you understand the sequence term \(a_k\), the sigma tells you which terms to include. The lower limit gives the starting index, and the upper limit gives the ending index.
This is where sequence knowledge develops into series knowledge. Arithmetic series use arithmetic sequence terms. Geometric series use geometric sequence terms. Taylor and Maclaurin series use sequences of coefficients and powers to represent functions. If you are moving into calculus, the pages on Taylor series and Maclaurin series, Maclaurin series, and the integral test and p-series are natural next steps.
Quick Sequence Calculator
Use this small checker to calculate an nth term and a finite sum for basic arithmetic or geometric sequences. It is designed for quick verification, not as a replacement for showing method in classwork. Enter the first term, common difference or ratio, and the term position \(n\).
Worked Sequence Examples
The best way to learn sequences is to classify the pattern before selecting a formula. Many wrong answers happen when students see numbers increasing and immediately assume an arithmetic sequence, or see terms becoming larger and immediately assume a geometric sequence. Slow down for one line of testing: check differences, check ratios, and check whether a second difference is constant.
Example 1: Find a Missing Arithmetic Term
The sequence \(9, 14, x, 24, 29\) is arithmetic. Find \(x\).
The common difference is \(14 - 9 = 5\). Therefore the third term must be \(14 + 5 = 19\). Check: \(19 + 5 = 24\) and \(24 + 5 = 29\). So \(x = 19\).
Example 2: Find the Position of a Term
In the arithmetic sequence \(8, 15, 22, 29, \ldots\), which term is \(141\)?
Here \(a_1 = 8\), \(d = 7\), and \(a_n = 141\). Use:
\[ 141 = 8 + (n - 1)7 \] \[ 133 = 7(n - 1) \] \[ 19 = n - 1 \] \[ n = 20 \]So \(141\) is the twentieth term.
Example 3: Geometric Decay
A ball rebounds to \(\frac{3}{5}\) of its previous height. It is dropped from \(125\) cm. What is the height after the fourth rebound?
This is geometric because each rebound is a fixed fraction of the previous height. If \(a_1\) is the height after the first rebound, then \(a_1 = 125 \cdot \frac{3}{5} = 75\). The common ratio is \(r = \frac{3}{5}\). The fourth rebound height is:
\[ a_4 = 75\left(\frac{3}{5}\right)^3 \] \[ a_4 = 75 \cdot \frac{27}{125} = 16.2 \]The height after the fourth rebound is \(16.2\) cm.
Example 4: Arithmetic Series Total
A student saves \(12\) dollars in week \(1\), \(17\) dollars in week \(2\), \(22\) dollars in week \(3\), and continues increasing the amount by \(5\) dollars each week. How much is saved in \(20\) weeks?
This is an arithmetic sequence with \(a_1 = 12\), \(d = 5\), and \(n = 20\). Use:
\[ S_n = \frac{n}{2}\left(2a_1 + (n - 1)d\right) \] \[ S_{20} = \frac{20}{2}\left(2(12) + 19(5)\right) \] \[ S_{20} = 10(24 + 95) = 1190 \]The student saves \(1190\) dollars in total.
Example 5: Infinite Geometric Series
Find the sum of \(18 + 12 + 8 + \frac{16}{3} + \cdots\), if it exists.
The common ratio is \(r = \frac{12}{18} = \frac{2}{3}\). Since \(|r| \lt 1\), the infinite sum exists. Use:
\[ S_{\infty} = \frac{a_1}{1 - r} \] \[ S_{\infty} = \frac{18}{1 - \frac{2}{3}} = \frac{18}{\frac{1}{3}} = 54 \]The infinite sum is \(54\).
Example 6: Quadratic nth Term
Find the nth term of \(2, 7, 16, 29, 46, \ldots\).
First differences are \(5, 9, 13, 17, \ldots\). Second differences are \(4, 4, 4, \ldots\), so \(2A = 4\) and \(A = 2\). Compare with \(2n^2\):
When \(n = 1\), \(2n^2 = 2\), difference \(0\). When \(n = 2\), \(2n^2 = 8\), difference \(-1\). When \(n = 3\), \(2n^2 = 18\), difference \(-2\). The remaining pattern is \(1 - n\). Therefore:
\[ a_n = 2n^2 - n + 1 \]Check \(n = 4\): \(2(16) - 4 + 1 = 29\), which matches the sequence.
Real-World Uses of Sequences
Sequences matter because many real systems change in regular steps. They are not just classroom patterns. A salary that rises by the same amount each year is arithmetic. A bank balance growing by a fixed percentage is geometric. A staircase design may use triangular numbers. A recursive model may represent a population where each generation depends on the one before it.
Finance and Compound Interest
Compound interest is one of the clearest applications of geometric sequences. If an account starts with principal \(P\) and grows by rate \(i\) each period, the balance after \(n\) periods is often modeled by:
Each period multiplies the previous balance by \(1 + i\). That multiplier is the common ratio. This is why percentage growth belongs with geometric sequences rather than arithmetic sequences. RevisionTown's compound interest formula page and compound interest formula guide extend this idea into finance-focused problems.
Computer Science and Recursion
Recursive thinking appears in programming whenever a result is built from earlier results. Fibonacci numbers, dynamic programming, search trees, and iterative approximations all use sequence logic. Even if a program does not display a sequence of numbers to the user, the algorithm may still generate intermediate terms internally.
Science and Growth Models
Biology, chemistry, and physics often use sequences to represent repeated time steps. A bacteria population might double each hour under ideal conditions. A medicine concentration might decay by a fixed percentage each hour. A radioactive sample might lose a fixed fraction over each half-life. In all these cases, the key question is whether change is additive, multiplicative, or governed by a more complex recurrence.
Statistics and Time Series
When data is recorded over time, the ordered nature of the data matters. Monthly sales, daily temperatures, yearly population values, and hourly website traffic are all sequences in a broad sense. A formal statistics course treats them as time series. If you are heading in that direction, see RevisionTown's time series analysis resource after you are comfortable with basic sequence notation.
How to Solve Sequence Questions Efficiently
Most sequence questions become easier when you follow a consistent diagnostic routine. The goal is not to memorize dozens of separate tricks. The goal is to identify the structure fast, then choose the formula that matches that structure.
Step 1: Write the Position Numbers
Place \(n = 1, 2, 3, 4, \ldots\) above the terms. Many students skip this because the sequence looks simple. But when the question asks for \(a_{50}\), \(S_{20}\), or the position of a given term, position numbers prevent confusion. They also help you see whether the first listed term is treated as \(a_1\) or \(a_0\).
Step 2: Test Differences
Subtract consecutive terms. If the differences are constant, the sequence is arithmetic. If the differences are not constant, check second differences. Constant second differences suggest a quadratic sequence. If third differences become constant, the pattern may be cubic, although many school courses stop at quadratic sequences.
Step 3: Test Ratios
If the terms are nonzero, divide each term by the previous term. If the ratios are constant, the sequence is geometric. Be careful with negative ratios because signs alternate. Be careful with fractions because a shrinking geometric sequence is still geometric.
Step 4: Decide Whether You Need a Term or a Sum
Questions about \(a_n\) ask for a term. Questions about \(S_n\), totals, accumulated values, or "how much altogether" usually ask for a sum. Mixing term formulas and sum formulas is one of the easiest ways to lose marks. Before calculating, underline whether the problem asks for a single term or a total.
Step 5: Check the Answer Against the Pattern
After finding a formula, test it on at least two terms from the original sequence. If the rule produces the first term but not the second or third, your indexing or simplification is wrong. A quick check catches most mistakes before they reach the final answer line.
Sequence Word Problems and Model Building
Word problems are often harder than pure number patterns because the sequence is hidden inside a situation. The numbers may represent weeks, payments, rows, years, bounces, memberships, or stages in a design. Before writing a formula, identify what one term represents. Is \(a_n\) the amount saved in week \(n\), the total amount saved by week \(n\), the height after bounce \(n\), or the number of tiles in pattern \(n\)? This distinction controls whether you need a term formula or a sum formula.
A reliable way to begin is to write a small table with two columns: position and value. Use the wording to decide the position. If a problem says "in the first month," that is usually \(n = 1\). If it says "after zero months," that is \(n = 0\). Many finance and science problems start at time \(0\), while many school pattern problems start at term \(1\). Do not force every situation into \(a_1\) without checking the language.
Recognizing Additive Change
Look for wording such as "increases by 8 each week," "decreases by 12 each year," "adds the same number," or "the next row has 3 more." These phrases usually signal an arithmetic sequence. The common difference is the fixed change. If a library has \(1200\) books and adds \(75\) books per month, the number of books after each completed month follows an arithmetic pattern because the same amount is added each time.
A club has \(35\) members in January and gains \(6\) members each month. If January is month \(1\), the membership in month \(n\) is:
\[ a_n = 35 + (n - 1)6 \]If the question asks for the membership in month \(10\), use \(a_{10}\). If it asks for the total number of monthly membership counts recorded from January through October, use \(S_{10}\). In most practical contexts, those are very different questions.
Recognizing Multiplicative Change
Look for wording such as "multiplies by," "doubles," "halves," "grows by 5 percent," "falls by 20 percent," or "keeps 80 percent." These phrases usually signal a geometric sequence. A percentage increase of \(5\) percent means multiply by \(1.05\). A percentage decrease of \(20\) percent means multiply by \(0.80\). Students often subtract the percentage as if the same amount is lost each time, but percentage change is based on the current value, so it is multiplicative.
A phone is worth \(900\) dollars when new and loses \(18\) percent of its value each year. If \(n\) counts the number of years after purchase, then the value after \(n\) years is:
\[ V_n = 900(0.82)^n \]This formula starts at \(n = 0\), so \(V_0 = 900\). If your course requires first-term notation, you could define \(a_1 = 900(0.82)\) as the value after the first year, but then the formula would shift. The mathematics is the same; the indexing is different.
Pattern Diagrams and Figurate Sequences
Diagram questions often show pattern \(1\), pattern \(2\), pattern \(3\), and ask for a formula for pattern \(n\). Start by counting the objects in each visible pattern. Then test differences. If the first differences are constant, the diagram is likely arithmetic. If the second differences are constant, it is likely quadratic. For tile patterns, matchsticks, dots, squares, and layered designs, a quadratic rule is common because the shape grows in two directions.
There are two good methods for pattern diagrams. The first is numerical: count the terms and use differences. The second is structural: split the shape into rectangles, lines, corners, or overlapping parts and write a formula from the geometry of the picture. The structural method often produces stronger explanations because it shows why the rule works, not just which formula fits the first few terms.
Totals, Accumulation, and Running Sums
Some word problems describe individual terms, while others describe accumulated totals. Suppose a worker earns \(50\) dollars on day \(1\), \(55\) dollars on day \(2\), \(60\) dollars on day \(3\), and so on. The amount earned on day \(n\) is a term. The total earned over the first \(n\) days is a series. If the question says "on day \(20\)," find \(a_{20}\). If it says "during the first \(20\) days," find \(S_{20}\). That one word, "during," often changes the entire calculation.
For extra mixed practice after this guide, the math worksheet generator can help you create more arithmetic and algebra questions, while Understanding Sequences and Series gives another explanation of the connection between individual terms and sums.
Practice Questions with Short Answers
Use these questions to check whether you can classify sequence types and select the correct formula without being told which method to use. Try writing the first line of working before looking at the answer. For most sequence questions, the first line should identify \(a_1\), \(d\), \(r\), or the differences.
Find the nth term of \(10, 16, 22, 28, \ldots\).
Answer: The sequence is arithmetic with \(a_1 = 10\) and \(d = 6\), so \(a_n = 10 + (n - 1)6 = 6n + 4\).
Find the tenth term of \(4, 12, 36, 108, \ldots\).
Answer: The sequence is geometric with \(a_1 = 4\) and \(r = 3\). Therefore \(a_{10} = 4(3)^9 = 78732\).
The sequence \(7, 11, 15, 19, \ldots\) continues. Find the sum of the first \(30\) terms.
Answer: Here \(a_1 = 7\), \(d = 4\), and \(n = 30\). Use \(S_n = \frac{n}{2}\left(2a_1 + (n - 1)d\right)\). Then \(S_{30} = 15(14 + 116) = 1950\).
Find the nth term of \(6, 13, 24, 39, 58, \ldots\).
Answer: First differences are \(7, 11, 15, 19, \ldots\). Second differences are \(4, 4, 4, \ldots\), so the rule is quadratic with \(A = 2\). Comparing with \(2n^2\) leaves \(4, 5, 6, 7, \ldots\), which is \(n + 3\). Therefore \(a_n = 2n^2 + n + 3\).
Does the infinite geometric series with \(a_1 = 24\) and \(r = -\frac{3}{4}\) have a finite sum? If so, find it.
Answer: Since \(\left|-\frac{3}{4}\right| \lt 1\), the infinite sum exists. Use \(S_{\infty} = \frac{a_1}{1 - r}\). Then \(S_{\infty} = \frac{24}{1 - \left(-\frac{3}{4}\right)} = \frac{24}{\frac{7}{4}} = \frac{96}{7}\).
A theatre has \(18\) seats in the first row and each next row has \(4\) more seats than the row before it. How many seats are in row \(25\)?
Answer: This is arithmetic with \(a_1 = 18\), \(d = 4\), and \(n = 25\). The row has \(a_{25} = 18 + 24(4) = 114\) seats.
A rumor reaches \(5\) people on day \(1\), then triples each day. How many people hear it on day \(8\), assuming the model continues exactly?
Answer: This is geometric with \(a_1 = 5\), \(r = 3\), and \(n = 8\). Therefore \(a_8 = 5(3)^7 = 10935\).
Expand \(\sum_{k=2}^{5} k^2\) and find its value.
Answer: The sum is \(2^2 + 3^2 + 4^2 + 5^2 = 4 + 9 + 16 + 25 = 54\).
Common Mistakes with Sequences
Sequence problems often look short, but they are full of small traps. These are the errors to watch for when preparing for tests or writing final solutions.
Study Path for Different Courses
Sequences appear at different levels of difficulty depending on the course. A younger student may only need to continue patterns and identify simple nth terms. A GCSE or IGCSE student may need arithmetic, geometric, and quadratic rules. An A-Level, IB, or AP student may need sigma notation, series sums, convergence tests, and links to functions.
If you are building foundations, start with arithmetic sequences and geometric sequences. Then add quadratic sequences once you are comfortable with differences. After that, learn sigma notation and the difference between a sequence and a series. Students preparing for advanced courses should connect this page with algebra learning resources, free math resources, and formula sheets.
For curriculum-specific revision, use the level that matches your course. The sitemap-verified sequence pages include sequences for seventh grade, sequences for eighth grade, sequences for ninth grade, sequences for eleventh grade, and sequences for twelfth grade. For broader course hubs, continue with GCSE maths, A-Level maths formula sheet, IB Mathematics, AP Mathematics, or SAT Mathematics.
Essential Sequence Formulae
Use this table as a quick reference after you understand the reasoning behind each formula. Memorizing formulas without recognizing the pattern is risky, but a concise formula list is valuable for revision.
| Topic | Formula | Use when |
|---|---|---|
| Arithmetic nth term | \(a_n = a_1 + (n - 1)d\) | Consecutive terms have constant difference \(d\) |
| Arithmetic sum | \(S_n = \frac{n}{2}(a_1 + a_n)\) | You know the first term, last term, and number of terms |
| Arithmetic sum with \(d\) | \(S_n = \frac{n}{2}\left(2a_1 + (n - 1)d\right)\) | You know the first term, common difference, and number of terms |
| Geometric nth term | \(a_n = a_1r^{n - 1}\) | Consecutive nonzero terms have constant ratio \(r\) |
| Finite geometric sum | \(S_n = \frac{a_1(1 - r^n)}{1 - r}\) | You need the total of the first \(n\) geometric terms and \(r \ne 1\) |
| Infinite geometric sum | \(S_{\infty} = \frac{a_1}{1 - r}\) | The common ratio satisfies \(|r| \lt 1\) |
| Quadratic nth term | \(a_n = An^2 + Bn + C\) | The second differences are constant |
| Triangular numbers | \(T_n = \frac{n(n + 1)}{2}\) | You are adding \(1 + 2 + 3 + \cdots + n\) |
| Fibonacci recurrence | \(F_n = F_{n-1} + F_{n-2}\) | Each term is the sum of the previous two terms |
Frequently Asked Questions
What is the easiest way to identify a sequence type?
Check first differences, then ratios, then second differences. Constant first differences indicate an arithmetic sequence. Constant ratios indicate a geometric sequence. Constant second differences indicate a quadratic sequence. If none of these work, the sequence may be recursive, special, or based on a less common rule.
What is the difference between \(a_n\) and \(S_n\)?
\(a_n\) is a single term in position \(n\). \(S_n\) is the sum of the first \(n\) terms. For example, if the sequence is \(2, 4, 6, 8, \ldots\), then \(a_4 = 8\), but \(S_4 = 2 + 4 + 6 + 8 = 20\).
Can a sequence be both arithmetic and geometric?
Yes, but only in special cases. A constant nonzero sequence such as \(5, 5, 5, 5, \ldots\) is arithmetic with \(d = 0\) and geometric with \(r = 1\). A sequence of all zeros is arithmetic, but the geometric ratio is not well-defined because division by zero is involved.
Why do geometric formulas use powers?
Geometric sequences multiply by the same ratio repeatedly. Repeated multiplication is represented by exponents. If the first term is \(a_1\), then the second term has one multiplication by \(r\), the third has two, and the \(n\)-th has \(n - 1\). That gives \(a_n = a_1r^{n - 1}\).
How do sequence questions connect to functions?
A sequence can be treated as a function whose input is a positive integer. The rule \(a_n = 3n + 2\) is like a function \(f(n) = 3n + 2\), but the input values are usually limited to whole-number positions. This is why sequences connect naturally to linear, exponential, and quadratic functions.
What should I practice after this guide?
Practice mixed recognition problems first. Then move to sums, word problems, recursive definitions, and sigma notation. Once those are comfortable, continue to series and convergence. You can also use RevisionTown's math calculator page when you need quick computational support while studying.
1.1.1 Arithmetic sequence
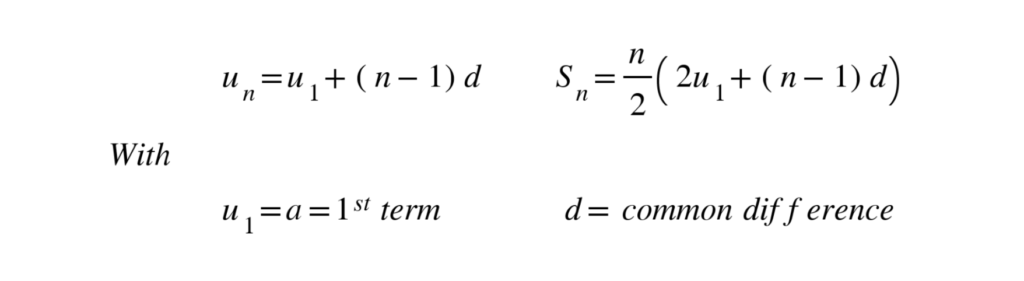
Often the IB requires you to first find the 1st term and/or common difference.
In an arithmetic sequence u10 = 37 and u22 = 1. Find the common difference and the first term.
- Put numbers in to nth term formula
37 = u1 + 9d
1 = u1 + 21d
2. Equate formulas to find d
21d −1=9d −37
12d = −36
d = −3
3. Use d to find u1
1 − 21 · (−3) = u1
u1 = 64
1.1.2 Geometric sequence
Geometric sequence the next term is the previous number multiplied by the common ratio (r).
To find the common ratio, divide any term of an arithmetic sequence by the term that precedes it, i.e.
DB 1.3 & 1.8 Use the following equations to calculate the nth term, the sum of n terms or the sum to infinity when −1 < r < 1.
Similar to questions on Arithmetic sequences, you are often required to find the 1st term and/or common ratio first.
1.1.3 Sigma notation
Sigma notation is a way to represent the summation of any sequence — this means that it can be used for both arithmetic or geometric series. The notation shows you the formula that generates terms of a sequence and the upper and lower limits of the terms that you want to add up in this sequence.
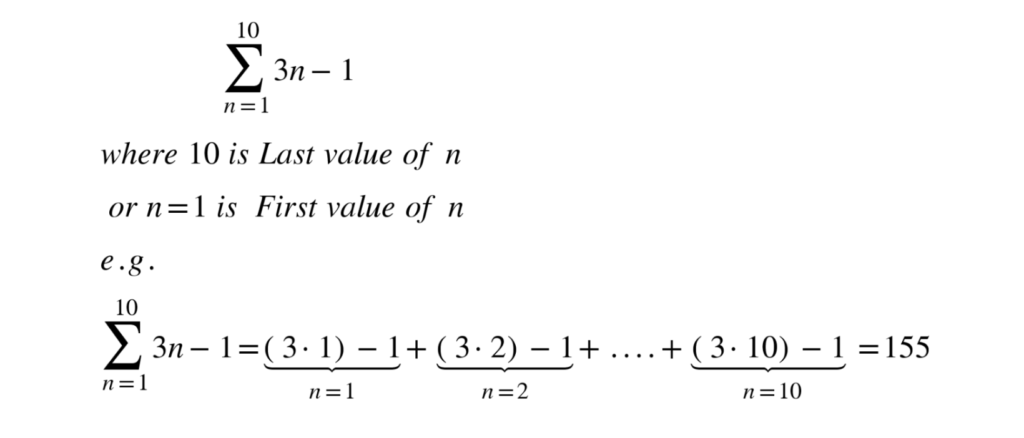
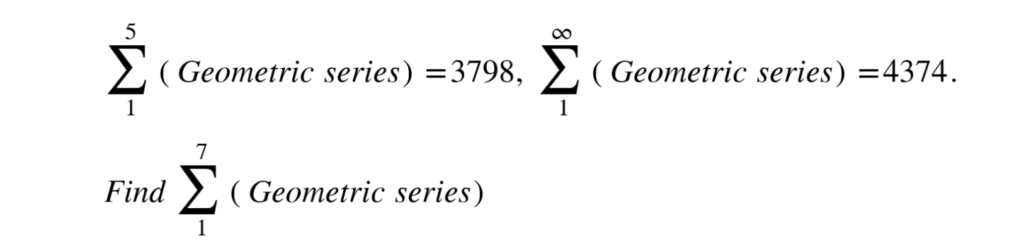
- Interpret the question
The sum of the first 5 terms of a geometric sequence is 3798 and the sum to infinity is 4374. Find the sum of the first 7 terms
2. Use formula for sum of n terms
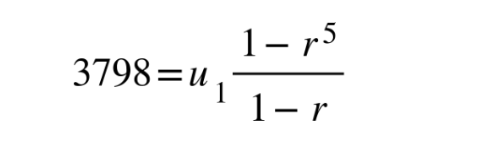
3. Use formula for sum to infinity
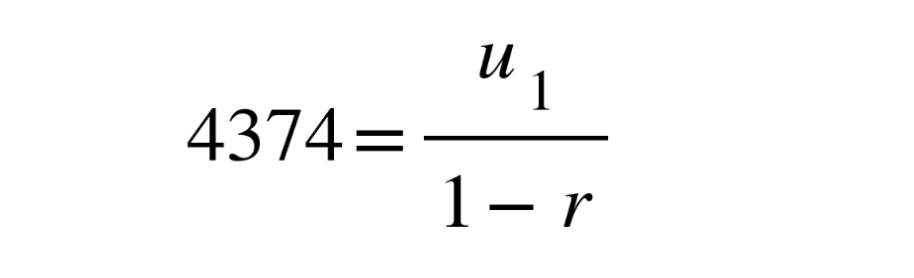
4. Rearrange 3. for u1
4374(1 − r ) = u1
5. Substitute in to 2.
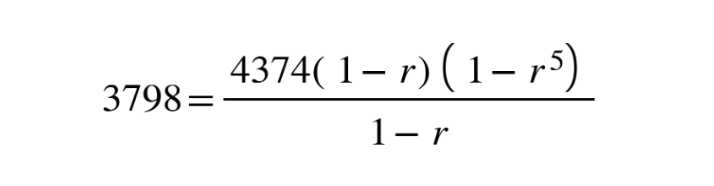
6. Solve for r
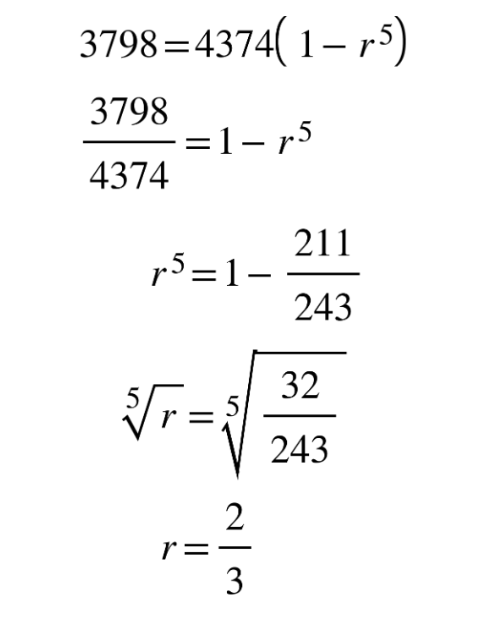
7. Use r to find u1
8. Find sum of first 7 terms
1.1.4 Compound interest
Sequences can be applied to many real life situations. One of those applications is calculating the interest of a loan or a deposit. Compound interest specifically deals with interest that is applied on top of previously calculated interest. For example, if you make a deposit in a bank and reinvest the interest you will gain even more interest next time. This happens because interest is calculated not just from your initial sum, but also including your re-investments.
DB 1.4
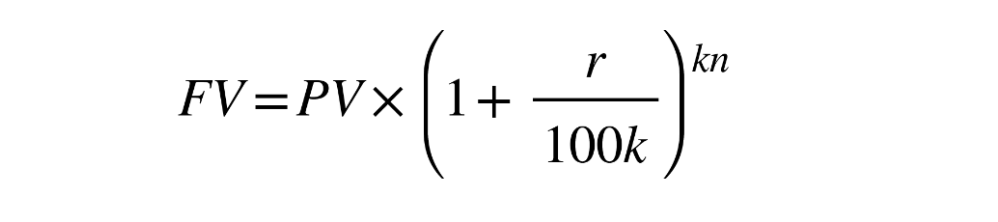
Where:
FV – is the future value,
PV – is the present value,
n – is number of years,
k – is the number of compounding periods per year,
r% – is the nominal annual rate of interest
Example: A deposit of 1000$ was made in a bank with annual interest of 3% that is compounded quarterly. Calculate the balance in 5 years.
We can use our compound interest equation. Let’s identify the known variables.
