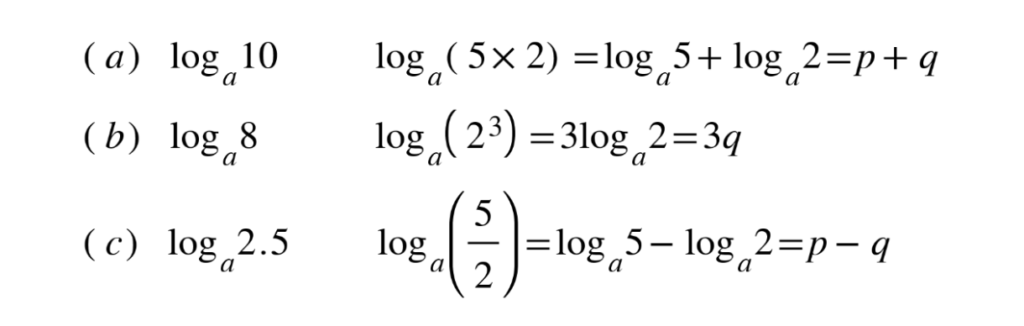1.2.1 Laws of exponents
Exponents always follow certain rules. If you are multiplying or dividing, use the following rules to determine what happens with the powers.
Example:
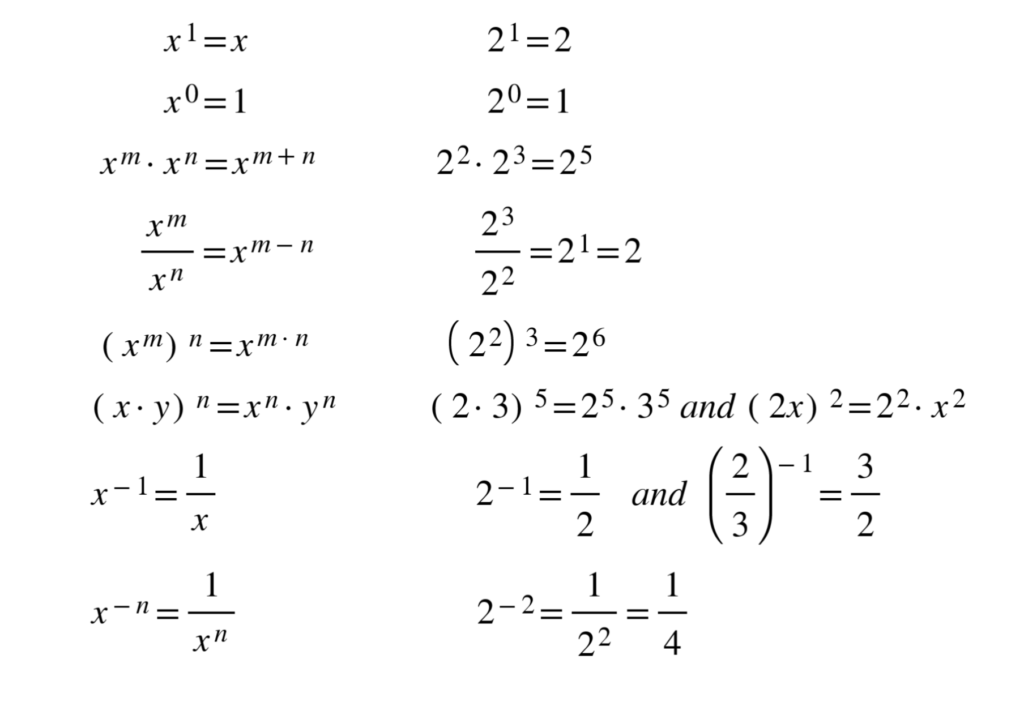
1.2.2 Fractional exponents
When doing mathematical operations (+, −, × or ÷) with fractions in the exponent you will need the following rules. These are often helpful when writing your answers in simplest terms.
Example:
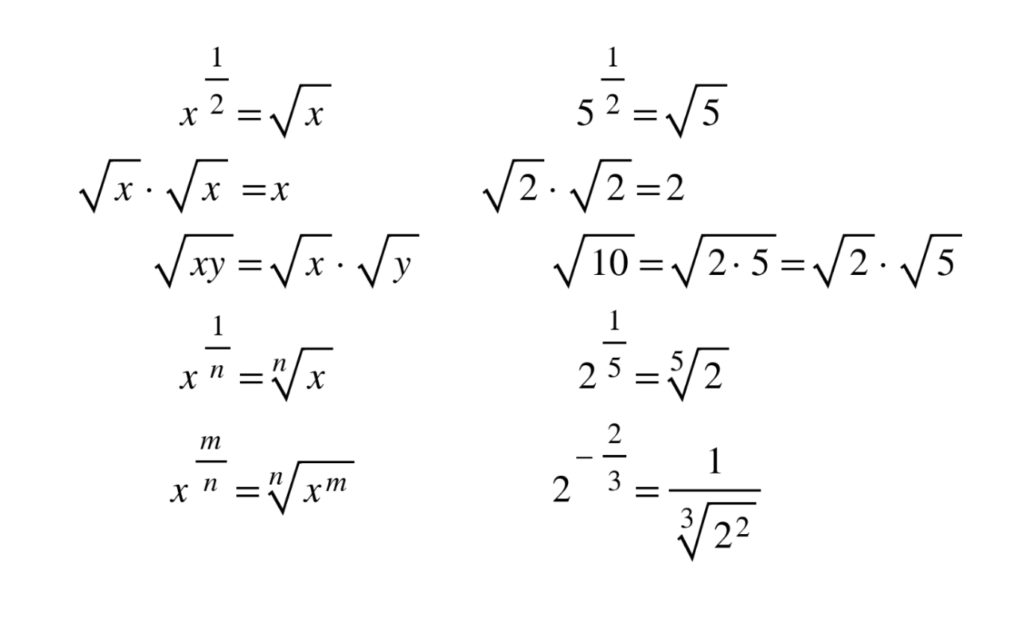
1.2.3 Laws of logarithms
Logarithms are the inverse mathematical operation of exponents, like division is the inverse mathematical operation of multiplication. The logarithm is often used to find the variable in an exponent.
DB 1.5 ax = b ⇔ x = Logab
Since loga ax = x, so then x = loga b.
This formula shows that the variable x in the power of the exponent becomes the subject of your log equation, while the number a becomes the base of your logarithm.
Logarithms with bases of 10 and e have special notations in which their base is not explicitly noted.
log10 x = log x
loge x = ln x
(Note: Remember that e is just the irrational number 2.71828…, so the same laws apply to ln as to other logarithms.)
Below are the rules that you will need to use when performing calculations with logarithms and when simplifying them. The sets of equations on the left and right are the same; on the right we show the notation that the formula booklet uses while the equations on the left are easier to understand.
Laws of logarithms and change of base
DB 1.7
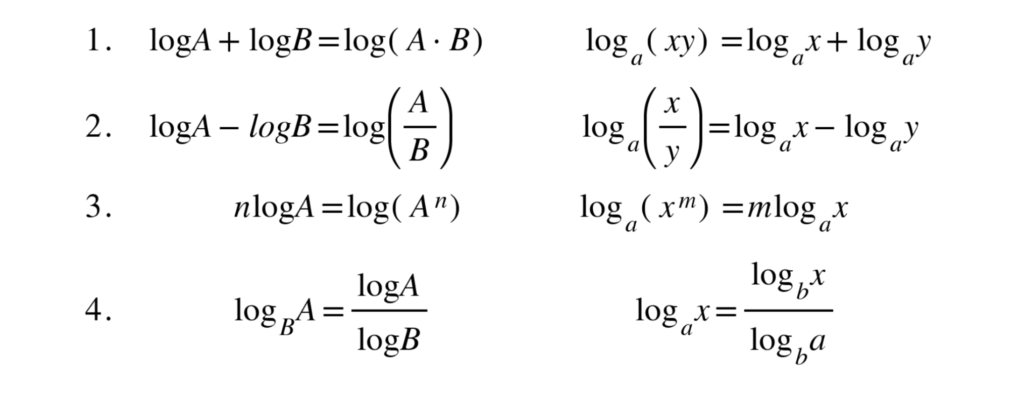
(Note: With the 4th rule you can change the base of a log)
Next to these rules, there are a few handy things to keep in mind when working with logarithms.
loga 0 = x is always undefined (because ax ≠ 0)
x = loga a = 1, which also means that ln e = 1
elna = a
Solve for x in the exponent using logarithms
Solve 2x = 13
- Take the log on both sides
2. Use rule III to take x outside
x log 2 = log 13
3. Solve
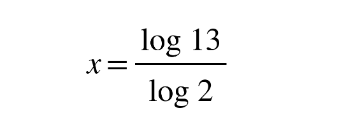
Expressing logs in terms of other logs
Example: Given that p = loga 5 and q = loga 2 express the following in terms of p and q