Binomial expansion

Binomial expression an expression (a + b)n which is the sum of two terms raised to the power n.

e.g. (x + 3)2

Binomial expansion (a + b)n expanded into a sum of terms

e.g. x2 + 6x + 9

Binomial expansions get increasingly complex as the power increases:

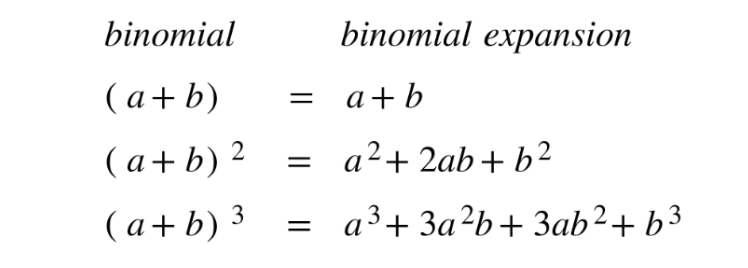
Binomial expansion

The general formula for each term in the expansion is nCr an-r br .

In order to find the full binomial expansion of a binomial, you have to determine the coefficient nCr and the powers for each term. The powers for an and b are found as n − r and r respectively, as shown by the binomial expansion formula.

Binomial expansion formula

DB 1.9

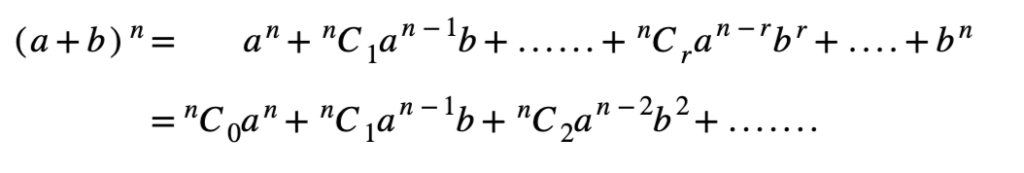
Binomial expansion formula

The powers decrease by 1 for a and increase by 1 for b for each subsequent term.

The sum of the powers of each term will always = n.
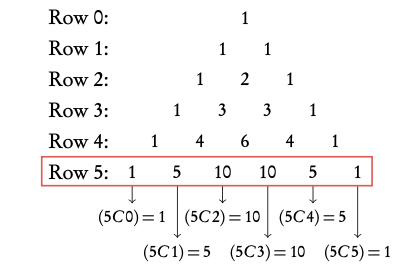
There are two ways to find the coefficients: with Pascal’s triangle or the binomial coefficient function (nCr). You are expected to know both methods.

Pascal’s triangle

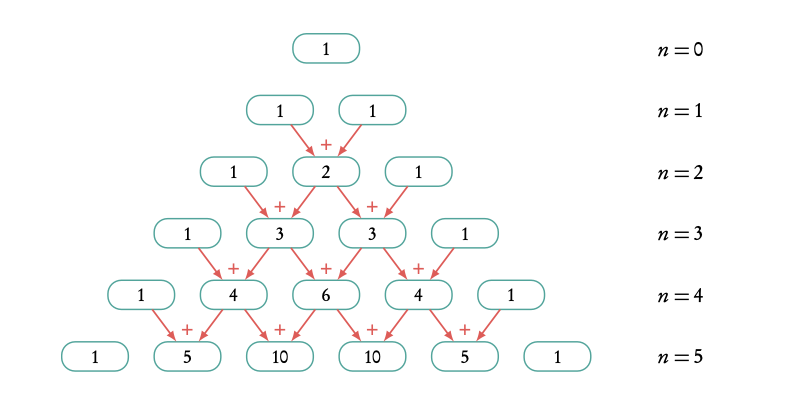
Pascal’s triangle 1

Pascal’s triangle is an easy way to find all the coefficients for your binomial expansion. It is particularly useful in cases where:

  1.  the power is not too high (because you have to write it out manually)
  2. you need to find all the terms in a binomial expansion

Binomial coefficient functions

The alternative is to calculate the individual coefficients using the nCr function on your calculator, or with the formula below.

(Note:In the 1st term of the expansion r = 0, in the 2nd term r = 1, . . .)

Binomial coefficient functions

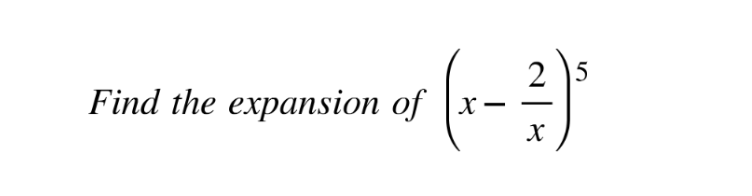
Expanding binomial expressions

Expanding binomial expressions

  1. Use the binomial expansion formula

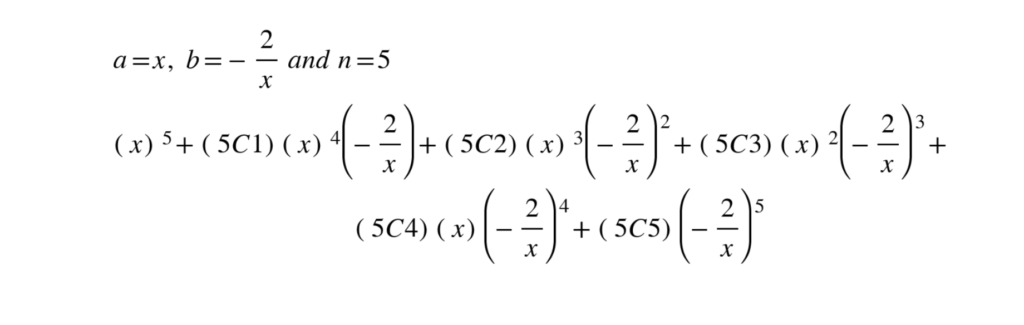
Expanding binomial expressions 1

2. Find coefficients using Pascal’s triangle for low powers or nCr on calculator for high powers

Expanding binomial expressions 2

3. Put the terms and their coefficients together

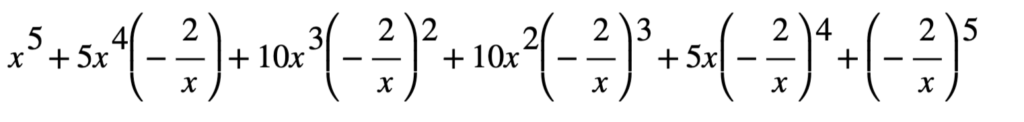
Expanding binomial expressions 3

4. Simplify using laws of exponents

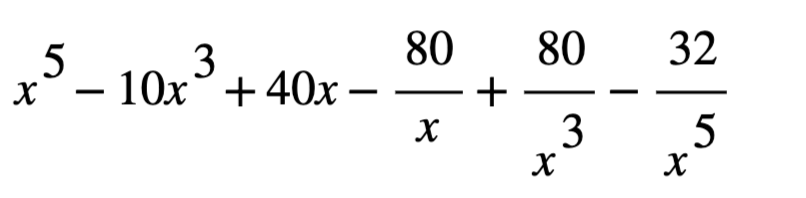
Expanding binomial expressions 4

Finding a specific term in a binomial expansion

Find the coefficient of x5 in the expansion of (2x − 5)8

  1. Use the binomial expansion formula

(a + b)n =··· + nCr an−r br +……

2. Determine r

Since a = 2x, to find x5 we need a5.

a5 = an−r = a8−r, so r = 3

3. Plug r into the general formula

nCr an−r br = 8C3 a8−3 b3 = 8C3 a5 b3

4. Replace a and b

8C3 (2x)5 (−5)3

5. Use nCr to calculate the value of the coefficient, nCr

8C3 = 8C3 = 56
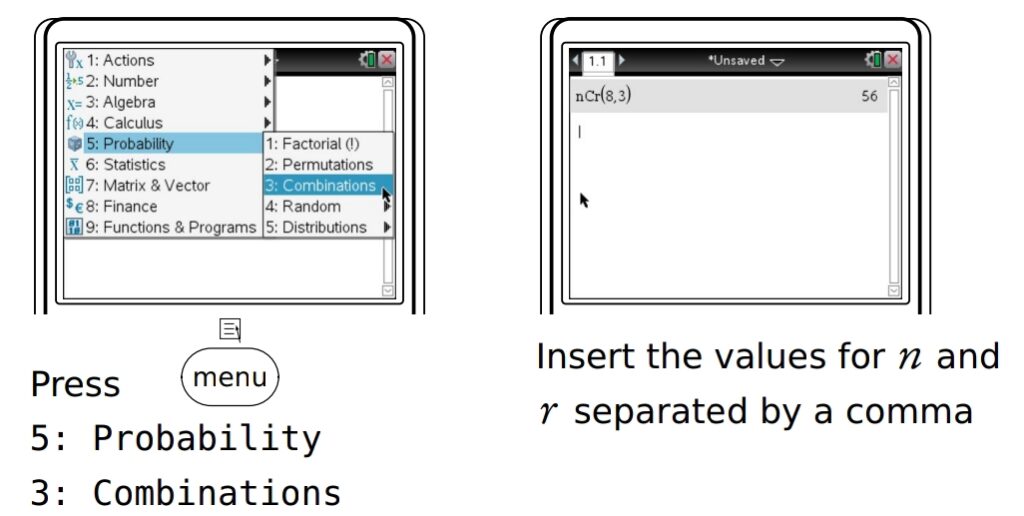
Finding a specific term in a binomial expansion

6. Substitute and simplify

56 × 25(x5) × (−5)3 = −224000(x5)

⇒ coefficient of x5 is −224000

The IB use three different terms for these types of question which will effect the answer you should give.

Coefficient the number before the x value
Term the number and the x value
Constant term the number for which there is no x value (x0)

Next Topic