Definitions
Function a mathematical relationship where each input has a single output. It is often written as f (x) where x is the input
Domain all possible x values, the input. (the domain of investigation)
Range possible y values, the output. (the range of outcomes)
Coordinates uniquely determines the position of a point, given by (x, y)
2.1. Types of functions
Linear functions y = m x + c
m is the gradient, c is the y intercept.
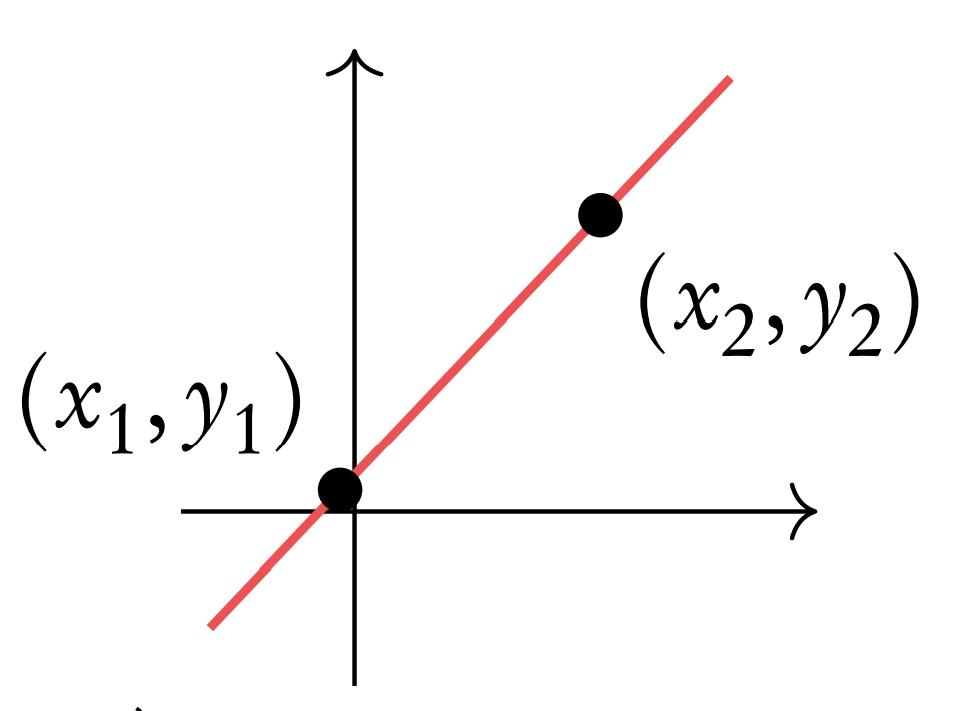

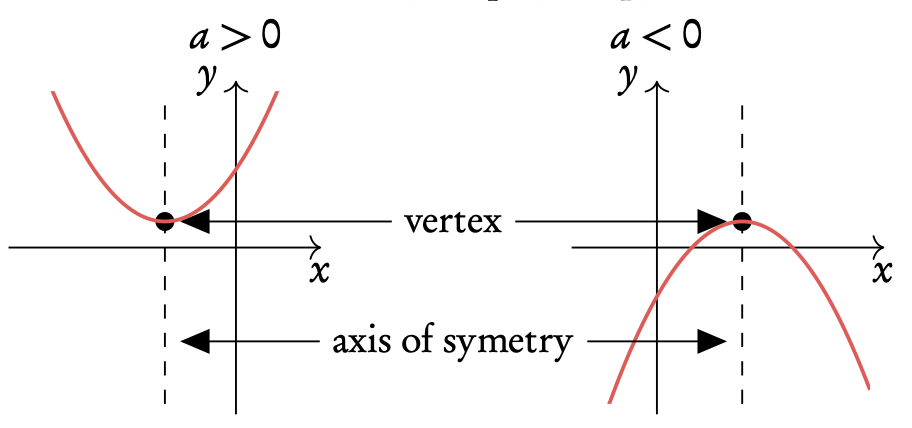
Quadratic functions y = ax2 + bx + c = 0
Axis of symmetry: x-coordinate of the vertex: x = −b/2a
Factorized form: y = (x + p)(x + q)
If a = 1 use the factorization method (x + p)·(x + q)
If a ≠ 1 use the quadratic formula
When asked excplicity complete the square
Vertex form: y = a(x − h)2 + k
Vertex: (h, k)
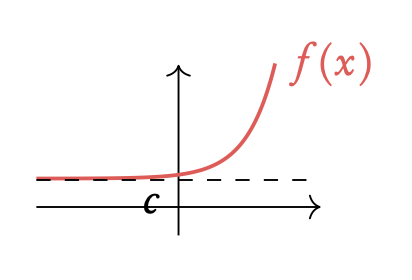
Exponential
f(x) = ax + c
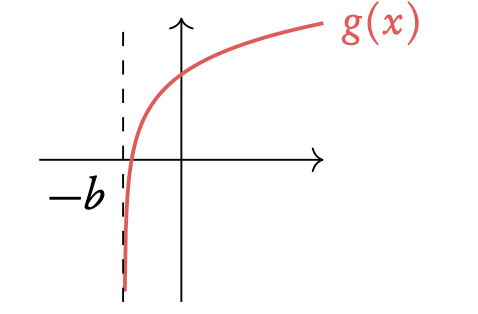
Logarithmic
g(x) = loga (x + b)
2.2. Rearranging functions
Inverse function, f −1(x) reflection of f (x) in y = x.
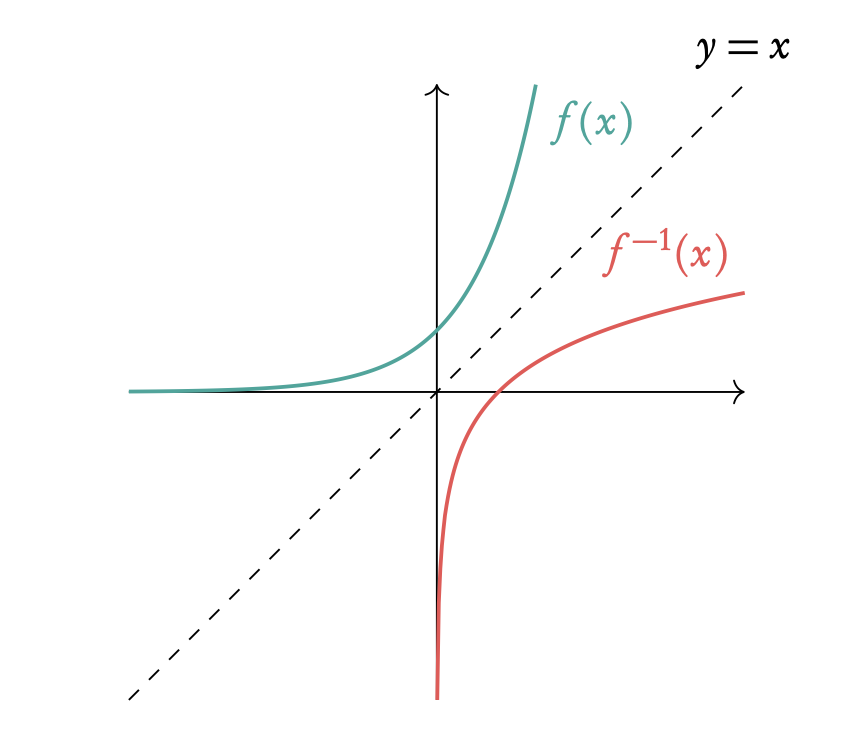
Composite function, (f ◦ g)(x) is the combined function f of g of x.
When f (x) and g(x) are given, replace x in f (x) by g(x).
Transforming functions

