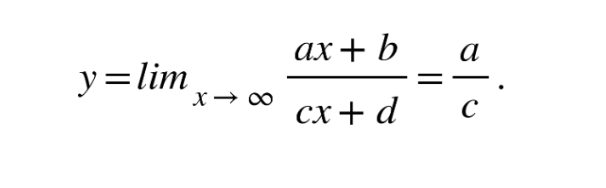Functions are mathematical relationships where each input has a single output. You have probably been doing functions since you began learning maths, but they may have looked like this:
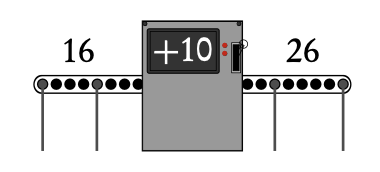
Algebraically this is:
f (x) = x + 10,
here x =16, y =26.
We can use graphs to show multiple outputs of y for inputs x, and therefore visualize the relation between the two. Two common types of functions are linear functions and quadratic functions.
2.1.1 Linear functions
Linear functions y = m x + c increases/decreases at a constant rate m, where m is the gradient and c is the y-intercept

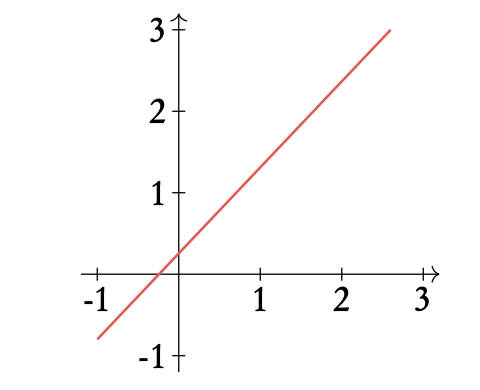
Straight line equations are sometimes written in two other forms, which you should be comfortable rearranging them to and from:
ax + by + d = 0 ⇒ general form
y − y1 = m(x − x1) ⇒ point-slope form
Example: Determine the midpoint, length and gradient of the straight line connecting the two points P1(2, 8) and P2(6, 3)
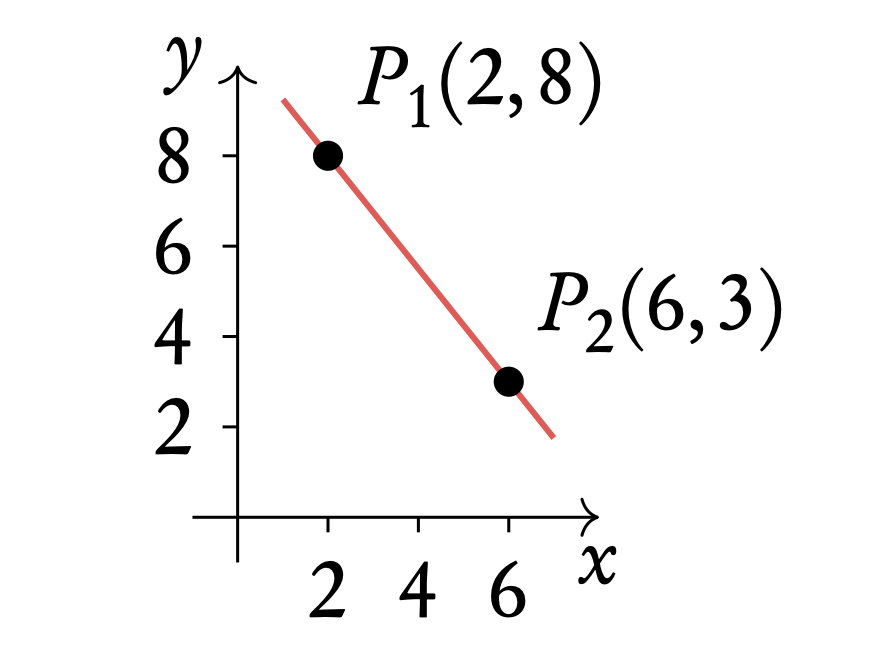

2.1.2 Quadratic functions
Graphed, quadratic functions make a parabolic shape; they increase/decrease at an increasing rate.
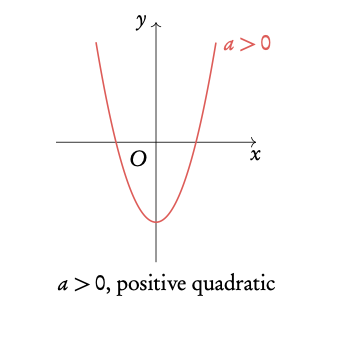
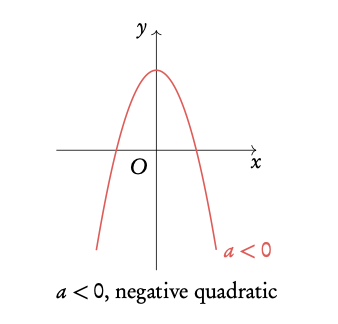
Quadratic functions y = ax2 + bx + c = 0
Axis of symmetry x = −b/2a = x−coordinate of vertex
Roots the x-intercept(s). Algebraically, roots can be found through factorisation or using the quadratic formula
Quadratic formula used to find the roots if a ≠ 1
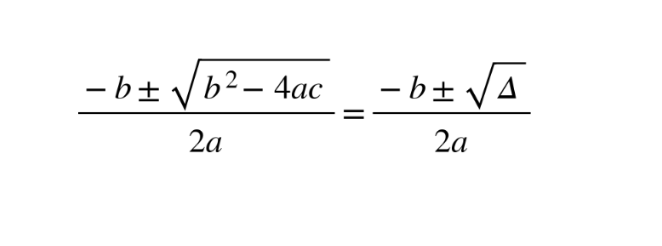
Discriminant ∆ the b2 − 4ac part of the formula, which can be used to determine how many x-intercepts a quadratic equation has
∆ > 0 ⇒ 2roots
∆ = 0 ⇒ 1root
∆ < 0 ⇒ no real roots
Note: Roots of quadratic equations are also referred to as ‘solutions’ or ‘zeros’.
Two more standard ways to write quadratic equations are:
y = a(x − h)2 + k with the vertex at (h, k)
y = a(x − p)(x − q) with x-intercepts (p, 0)(q, 0)
Solving quadratic equations by factorisation
Solve x2 − 5x + 6 = 0
- Set up a system of equations p + q = b and p × q = c
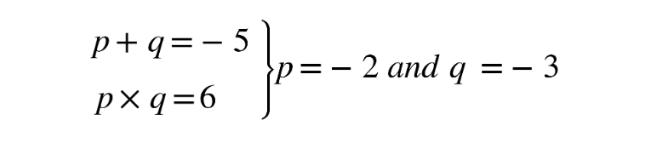
2. Plug the values for p and q into
(x + p)(x + q)
(x − 2)(x − 3) = x2 − 5x + 6
3. Equate each part to 0
(x + p) = 0, (x + q) = 0,
and solve for x
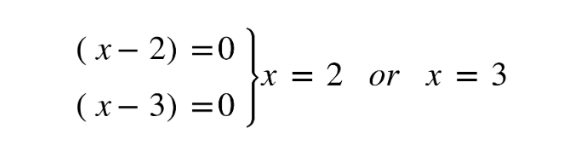
Solving quadratic equations using the quadratic formula
Solve 3x2 − 8x + 4 = 0
- Calculate the discriminant ∆ = b2 − 4ac
∆ = (−8)2 − 4 · 3 · 4 = 16
2. Use the discriminant to determine the number of solutions
∆ > 0 so 2 solutions
3. Find solutions using quadratic formula
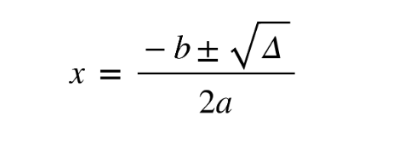
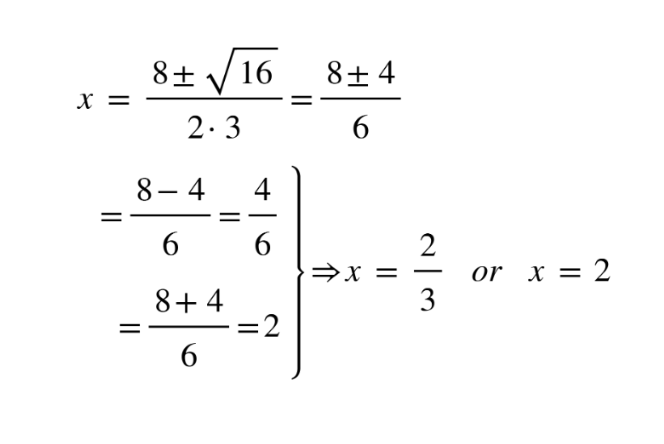
Through a method called completing the square, you can rearrange a quadratic function into the form y = a(x − h)2 + k. This way you can find the coordinates of the vertex (the minimum or maximum). For the exam you will always be asked explicitly to use this method.
Find the vertex by completing the square
- Move c to the other side
2. Divide by a
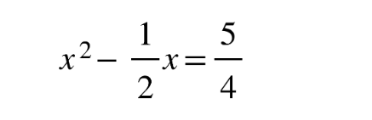
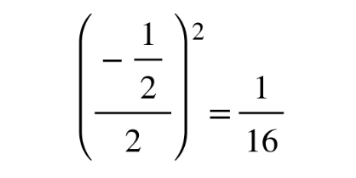
4. Add this term to both sides
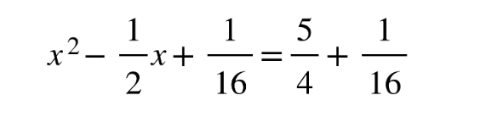
5. Factor perfect square and bring constant back
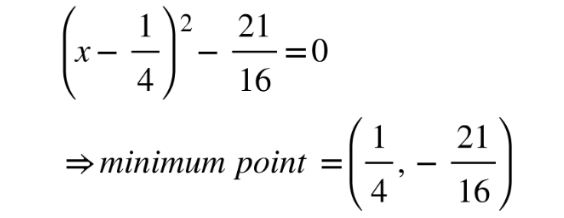
2.1.3 Functions with asymptotes
Asymptote a straight line that a curve approaches, but never touches.
A single function can have multiple asymptotes: horizontal, vertical and in rare cases diagonal. Functions that contain the variable (x) in the denominator of a fraction and exponential and logarithmic functions will always have asymptotes.
Vertical asymptotes
Vertical asymptotes occur when the denominator is zero, as dividing by zero is undefinable. Therefore if the denominator contains x and there is a value for x for which the denominator will be 0, we get a vertical asymptote.
Horizontal asymptotes
Horizontal asymptotes are the value that a function tends to as x becomes really big or really small; technically speaking to the limit of infinity, x → ∞. The general idea is then that when x is large, other parts of the function not involving x become insignificant and so can be ignored.
Example:
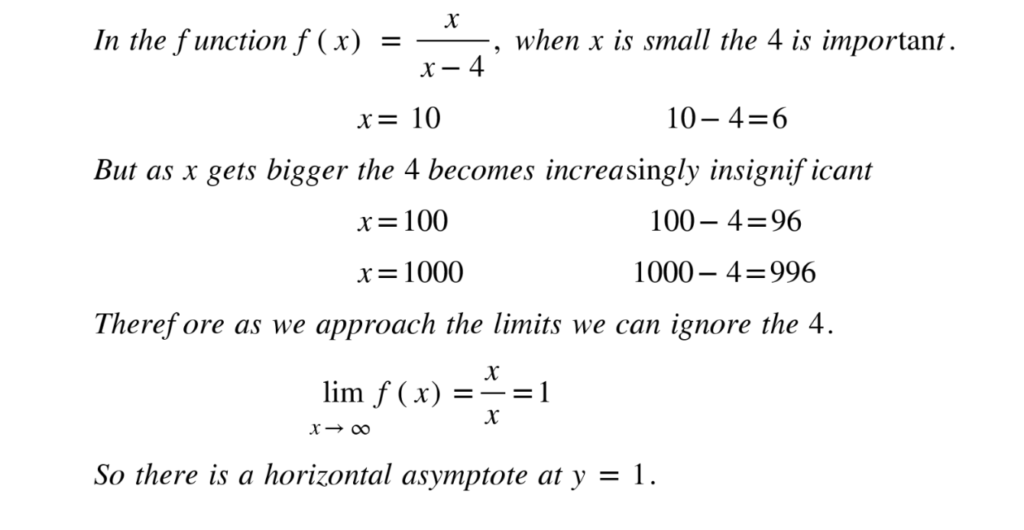
Exponential and logarithmic functions
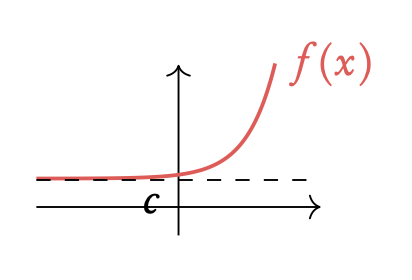
Exponential functions will always have a horizontal asymptote and logarithmic functions will always have a vertical asymptote, due to the nature of these functions. The position of the asymptote is determined by constants in the function.
Exponential
f(x) = ax + c asymptote at y = c
where a is a positive number (often e)
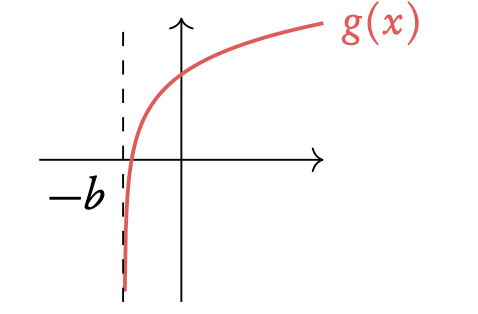
Logarithmic
g(x) = loga (x + b)
asymptote at x = −b
2.1.4 Special Functions
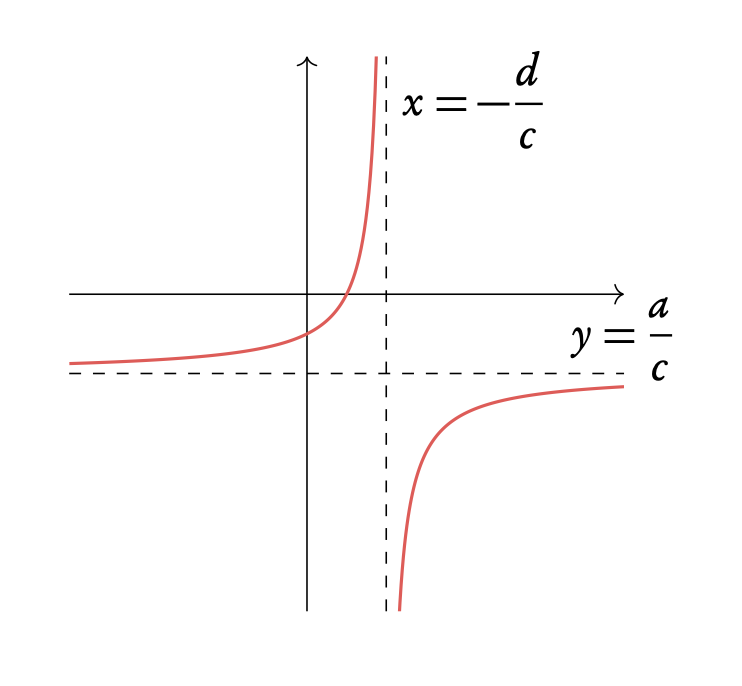
Rational function of the form y = (ax + b)/(cx +d)
The graph made by this function has one horizontal and one vertical asymptote. The graph is not continuous in all points, but splits into two parts. Both of the parts approach horizontal asymptote at either negative or positive large values of x and approach horizontal asymptote at either negative or positive large values of y. Also both parts are located in different “corners” of the coordinate system.
The vertical asymptote occurs where denominator is equal to 0, meaning x = −d/c . The graph is not defined at that point.
The horizontal asymptote occurs at very large values of x, meaning that asymptote occurs at