2.2.1 Inverse functions, f −1(x)
Inverse functions are the reverse of a function. Finding the input x for the output y. You can think of it as going backwards through the number machine.
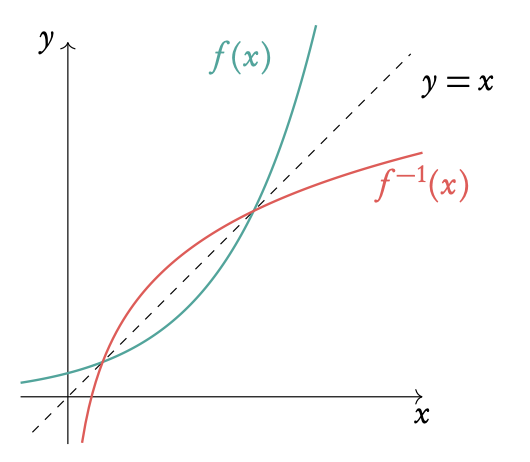
This is the same as reflecting a graph in the y = x axis.
Finding the inverse function.
f(x) = 2x3 + 3, find f −1(x)
Replace f(x) with y
y = 2x3 + 3
2. Solve for x
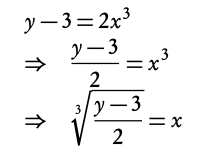
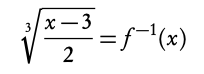
2.2.2 Composite functions
Composite functions are a combination of two functions.
(f ◦ g)(x) means f of g of x
To find the composite function above substitute the function of g(x) into the x of f (x).
Example: Let f(x) = 2x + 3 and g(x) = x2. Find (f ◦ g)(x) and (g ◦ f )(x).
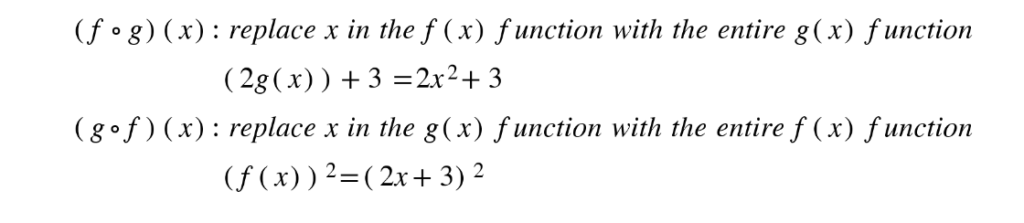
Note: Remember f ◦ g(x) ≠ g ◦ f(x)
2.2.3 Transforming functions
By adding and/or multiplying by constants we can transform a function into another function.

Exam hint: describe the transformation with words as well to guarantee marks.
Always do translations last
Transforming functions f (x) → af (x + b)
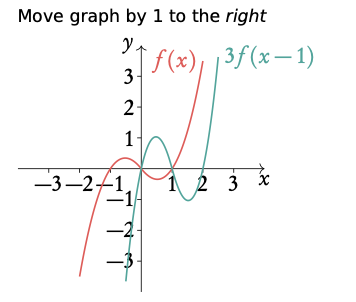
Given f(x)=¼ x3 + x2 − 5/4 x, draw 3f (x−1).
- Sketch f(x)
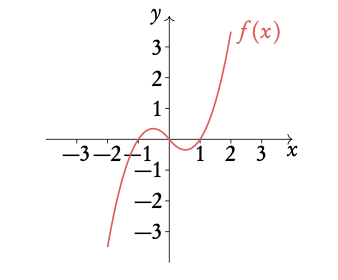
2. Stretch the graph by the factor of a
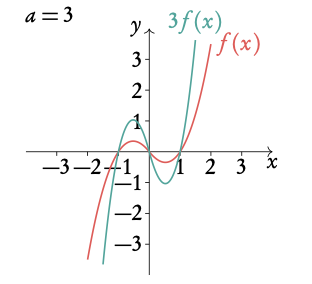
3. Move graph by −b