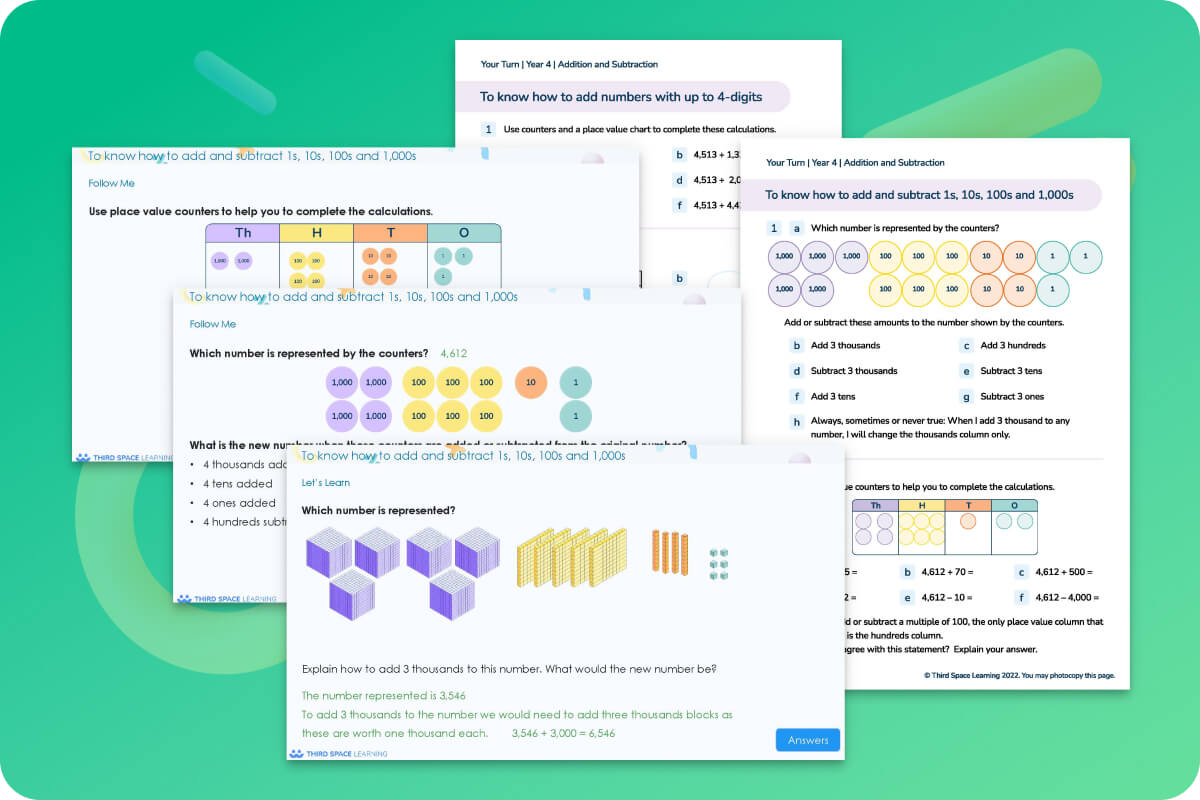
Mathematics is a fundamental subject that forms the backbone of various fields, from engineering and technology to finance and everyday problem-solving. Among the essential skills in mathematics are accurate calculations and a solid understanding of operational hierarchies, such as BODMAS. In this comprehensive guide, we delve into two primary resources in mathematics: using a calculator effectively and mastering BODMAS. This article is packed with high-trend keywords to ensure it remains relevant and accessible to learners, educators, and enthusiasts alike.
Calculator Activities & BODMAS: | ||
|
Introduction
Mathematics is often perceived as a challenging subject, but with the right tools and understanding, it becomes an engaging and manageable discipline. Two crucial aspects that aid in mastering mathematics are the effective use of calculators and the comprehension of operational hierarchies like BODMAS. Whether you’re a student, educator, or a lifelong learner, this guide will provide valuable insights into leveraging these resources to enhance your mathematical prowess.
The Importance of Calculations in Mathematics
Calculations are the building blocks of mathematics. They form the foundation for more complex concepts and problem-solving strategies. Accurate calculations ensure that mathematical models and theories are reliable, which is essential in fields such as engineering, physics, economics, and computer science. Moreover, proficiency in calculations enhances logical thinking and analytical skills, which are invaluable in everyday decision-making and problem-solving scenarios.
Using a Calculator Effectively
Calculators are indispensable tools in mathematics, facilitating complex computations and reducing the likelihood of human error. However, maximizing their utility requires understanding their functionalities and adopting best practices.
Types of Calculators
- Basic Calculators: Suitable for simple arithmetic operations like addition, subtraction, multiplication, and division.
- Scientific Calculators: Equipped with functions for trigonometry, logarithms, exponents, and other advanced mathematical operations.
- Graphing Calculators: Capable of plotting graphs, solving equations, and performing statistical analyses.
- Financial Calculators: Designed for financial calculations such as interest rates, loan payments, and investment returns.
- Programmable Calculators: Allow users to write and store custom programs for repetitive calculations.
Tips for Accurate Calculations
- Understand the Calculator: Familiarize yourself with the calculator’s functions and operations to utilize it effectively.
- Double-Check Entries: Always verify the numbers and operations entered to prevent errors.
- Use Parentheses: When performing complex calculations, use parentheses to ensure the correct order of operations.
- Clear Before Starting: Reset the calculator to avoid residual data affecting your current calculations.
- Battery Maintenance: Ensure your calculator has sufficient battery power to avoid interruptions during important calculations.
Common Calculator Functions
- Addition (+) and Subtraction (-)
- Multiplication (×) and Division (÷)
- Exponentiation (^)
- Square Roots (√)
- Logarithmic Functions (log, ln)
- Trigonometric Functions (sin, cos, tan)
- Memory Functions (M+, M-, MR, MC)
Advanced Calculator Features
- Graphing Capabilities: Plotting multiple functions simultaneously and analyzing their intersections.
- Equation Solvers: Solving linear, quadratic, and higher-degree equations.
- Statistical Analysis: Performing regression analysis, calculating standard deviations, and other statistical measures.
- Programming: Writing custom scripts to automate complex or repetitive calculations.
- Integration and Differentiation: Calculating integrals and derivatives for calculus applications.
Understanding BODMAS
BODMAS is an acronym representing the order of operations used to solve mathematical expressions. It stands for Brackets, Orders, Division and Multiplication, Addition and Subtraction. Understanding BODMAS is crucial for solving mathematical problems accurately and efficiently.
What is BODMAS?
BODMAS dictates the sequence in which operations should be performed to correctly evaluate a mathematical expression. It ensures consistency and avoids ambiguity in complex calculations.
Breaking Down BODMAS
- Brackets (B): Solve expressions inside parentheses (), braces {}, or brackets [] first.
- Orders (O): Calculate exponents (powers and roots) next.
- Division (D) and Multiplication (M): Perform these operations from left to right.
- Addition (A) and Subtraction (S): Finally, carry out addition and subtraction from left to right.
Importance of BODMAS in Mathematics
BODMAS provides a clear set of rules that eliminate confusion and ensure that mathematical expressions are interpreted consistently. It is essential for:
- Solving Complex Equations: Breaking down multi-step problems systematically.
- Programming and Algorithms: Ensuring that computational procedures follow the correct order of operations.
- Everyday Problem Solving: Facilitating accurate calculations in daily tasks like budgeting, cooking, and engineering projects.
BODMAS vs. PEMDAS
PEMDAS is another acronym similar to BODMAS, standing for Parentheses, Exponents, Multiplication and Division, Addition and Subtraction. The primary difference lies in the terminology:
- BODMAS: Brackets, Orders, Division/Multiplication, Addition/Subtraction.
- PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.
Both acronyms serve the same purpose, and the choice between them often depends on regional preferences.
Applying BODMAS in Calculations
Applying BODMAS correctly is vital for obtaining accurate results. Let’s explore step-by-step examples and common mistakes to avoid.
Step-by-Step Examples
Example 1:
Evaluate 7+3×(10/(12/(3+1)−1))7 + 3 \times (10 / (12 / (3 + 1) – 1))7+3×(10/(12/(3+1)−1))
Solution:
Brackets: Solve the innermost bracket first.
- 3+1=43 + 1 = 43+1=4
- Expression becomes 7+3×(10/(12/4−1))7 + 3 \times (10 / (12 / 4 – 1))7+3×(10/(12/4−1))
Orders: No exponents in this expression.
Division/Multiplication:
- 12/4=312 / 4 = 312/4=3
- 3−1=23 – 1 = 23−1=2
- 10/2=510 / 2 = 510/2=5
- 3×5=153 \times 5 = 153×5=15
Addition:
- 7+15=227 + 15 = 227+15=22
Final Answer: 22
Example 2:
Evaluate (5+3)×12/3(5 + 3) \times 12 / 3(5+3)×12/3
Solution:
Brackets:
- 5+3=85 + 3 = 85+3=8
- Expression becomes 8×12/38 \times 12 / 38×12/3
Division/Multiplication (from left to right):
- 8×12=968 \times 12 = 968×12=96
- 96/3=3296 / 3 = 3296/3=32
Final Answer: 32
Common Mistakes and How to Avoid Them
Ignoring Brackets: Not solving expressions inside brackets first can lead to incorrect results.
- Solution: Always identify and solve the innermost brackets before moving outward.
Incorrect Order of Operations: Performing operations out of sequence disrupts the calculation flow.
- Solution: Memorize the BODMAS/PEMDAS rules and apply them systematically.
Division and Multiplication Confusion: Treating division and multiplication as hierarchically different instead of performing them left to right.
- Solution: Remember that division and multiplication are of equal priority and should be executed in the order they appear from left to right.
Addition and Subtraction Errors: Similar to division and multiplication, these operations should be handled sequentially.
- Solution: Perform addition and subtraction in the order they appear, moving from left to right.
Misuse of Negative Numbers: Incorrect placement or handling of negative signs can alter the result.
- Solution: Pay careful attention to negative signs and ensure they are correctly incorporated into the calculation.
Integration of Calculators and BODMAS
Understanding BODMAS is essential when using calculators for complex expressions. While calculators can handle intricate calculations, inputting the expression correctly is crucial. Here’s how to integrate calculator use with BODMAS principles:
- Use Parentheses: When entering expressions into a calculator, use parentheses to ensure the correct order of operations.
- Break Down Complex Expressions: Simplify multi-step problems by breaking them into smaller parts and solving sequentially.
- Double-Check Results: Verify calculations by re-entering them or using different methods to ensure accuracy.
- Utilize Advanced Features: Leverage calculator functionalities like memory storage, equation solvers, and programmable functions to handle complex BODMAS applications efficiently.
FAQs
1. What does BODMAS stand for?
Answer: BODMAS is an acronym that stands for Brackets, Orders, Division and Multiplication, Addition and Subtraction. It represents the order of operations to be followed when solving mathematical expressions to ensure accuracy and consistency.
2. How is BODMAS different from PEMDAS?
Answer: BODMAS and PEMDAS both represent the order of operations in mathematics. BODMAS stands for Brackets, Orders, Division/Multiplication, Addition/Subtraction, while PEMDAS stands for Parentheses, Exponents, Multiplication/Division, Addition/Subtraction. The primary difference lies in terminology, with “Brackets” in BODMAS equivalent to “Parentheses” in PEMDAS, and “Orders” equivalent to “Exponents.”
3. Why is understanding BODMAS important in mathematics?
Answer: Understanding BODMAS is crucial because it provides a standardized sequence for performing operations in mathematical expressions, ensuring that calculations are accurate and consistent across different problems and contexts.
4. Can you give an example of a BODMAS calculation?
Answer: Sure! Evaluate 5+2×(32−1)5 + 2 \times (3^2 – 1)5+2×(32−1).
Solution:
- Brackets: 32−1=9−1=83^2 – 1 = 9 – 1 = 832−1=9−1=8
- Orders: 2×8=162 \times 8 = 162×8=16
- Addition: 5+16=215 + 16 = 215+16=21
Final Answer: 21
5. What are the different types of calculators used in mathematics?
Answer: The different types of calculators include Basic Calculators, Scientific Calculators, Graphing Calculators, Financial Calculators, and Programmable Calculators, each designed to handle varying levels of mathematical complexity.
6. How can I choose the right calculator for my needs?
Answer: Choose a calculator based on the complexity of the tasks you need to perform. For basic arithmetic, a simple calculator suffices. For advanced mathematics, sciences, or engineering, a scientific or graphing calculator is more appropriate. For financial calculations, a financial calculator is ideal, while programmable calculators are best for customized or repetitive tasks.
7. What are some essential features to look for in a scientific calculator?
Answer: Essential features include trigonometric functions, logarithms, exponents, parentheses handling, memory functions, and the ability to perform complex calculations involving multiple operations.
8. How do graphing calculators differ from scientific calculators?
Answer: Graphing calculators can plot graphs, solve equations graphically, and handle more complex functions, whereas scientific calculators focus on numerical computations and scientific functions without graphical capabilities.
9. What is the significance of the order of operations in programming?
Answer: In programming, the order of operations dictates how expressions are evaluated, ensuring that algorithms produce correct and predictable results. Ignoring this order can lead to bugs and logical errors in software applications.
10. How can I practice applying BODMAS effectively?
Answer: Practice by solving a variety of mathematical expressions with increasing complexity, ensuring you follow the BODMAS rules. Use worksheets, online quizzes, and mathematical software to reinforce your understanding.
11. Are there any online tools to help with BODMAS calculations?
Answer: Yes, there are numerous online calculators and educational platforms that allow you to input expressions and see step-by-step BODMAS calculations, such as Wolfram Alpha, Mathway, and various educational websites.
12. How does BODMAS apply to algebraic expressions?
Answer: In algebraic expressions, BODMAS ensures that operations are performed in the correct sequence, especially when variables and exponents are involved. This is crucial for simplifying expressions and solving equations accurately.
13. Can BODMAS be applied to calculus problems?
Answer: Yes, BODMAS is fundamental in calculus for performing operations like differentiation and integration, where the correct order of operations ensures accurate computation of derivatives and integrals.
14. What are common mistakes students make when using BODMAS?
Answer: Common mistakes include ignoring brackets, performing operations out of order, misapplying division and multiplication priorities, and mishandling negative numbers or exponents.
15. How can I avoid errors when using a calculator for BODMAS?
Answer: To avoid errors, always use parentheses to clarify the order of operations, double-check each step, use the calculator’s memory functions to store intermediate results, and ensure you’re familiar with the calculator’s syntax.
16. Is there a mnemonic to help remember BODMAS?
Answer: Yes, BODMAS itself is a mnemonic. Alternatively, some use “Brackets, Orders, Divide, Multiply, Add, Subtract” to remember the sequence of operations.
17. How does BODMAS help in solving real-life problems?
Answer: BODMAS provides a systematic approach to break down and solve complex problems, such as financial calculations, engineering designs, and data analysis, ensuring accuracy and efficiency in real-life applications.
18. What role do calculators play in enhancing mathematical learning?
Answer: Calculators aid in performing complex computations quickly, allowing learners to focus on understanding concepts and problem-solving strategies rather than manual calculation, thereby enhancing overall mathematical comprehension.
19. Can over-reliance on calculators hinder mathematical understanding?
Answer: Yes, excessive dependence on calculators can impede the development of fundamental calculation skills and conceptual understanding. It’s important to balance calculator use with manual problem-solving practice.
20. What are some advanced calculator functions that can aid in higher mathematics?
Answer: Advanced functions include symbolic computation, integration and differentiation, matrix operations, statistical analysis, graph plotting, and programming capabilities for custom calculations.
21. How can teachers integrate calculator use and BODMAS in the classroom?
Answer: Teachers can incorporate calculator-based activities that require students to apply BODMAS rules, create problem-solving exercises that involve multiple operations, and use calculators to demonstrate the importance of operation order in obtaining correct results.
22. What are the limitations of using calculators in mathematics?
Answer: Limitations include potential over-reliance leading to weak manual calculation skills, possible errors from incorrect input, and the inability to understand underlying mathematical concepts without proper guidance.
23. How can students improve their calculation skills alongside using calculators?
Answer: Students can enhance their skills by practicing manual calculations regularly, understanding the principles behind operations, solving problems without calculators to build foundational knowledge, and gradually integrating calculator use to handle more complex tasks.
24. Are there specific calculators recommended for different educational levels?
Answer: Yes. For primary education, basic calculators suffice. Middle and high school students may benefit from scientific calculators, while college and professional students, especially in STEM fields, often require graphing or programmable calculators.
25. How has technology influenced the way we perform mathematical calculations?
Answer: Technology has revolutionized mathematical calculations by providing powerful tools that handle complex computations swiftly and accurately, facilitating advanced research, enhancing educational methods, and enabling innovative applications across various industries.
Conclusion
Mastering mathematical calculations and understanding the order of operations through BODMAS are essential skills that empower individuals to solve problems accurately and efficiently. Utilizing calculators effectively complements these skills, providing a powerful combination for academic success and practical applications. By integrating these primary resources, learners can build a strong mathematical foundation, paving the way for advanced studies and professional excellence in diverse fields.