1.2.1 Laws of exponents
Exponents always follow certain rules. If you are multiplying or dividing, use the following rules to determine what happens with the powers.
Example:
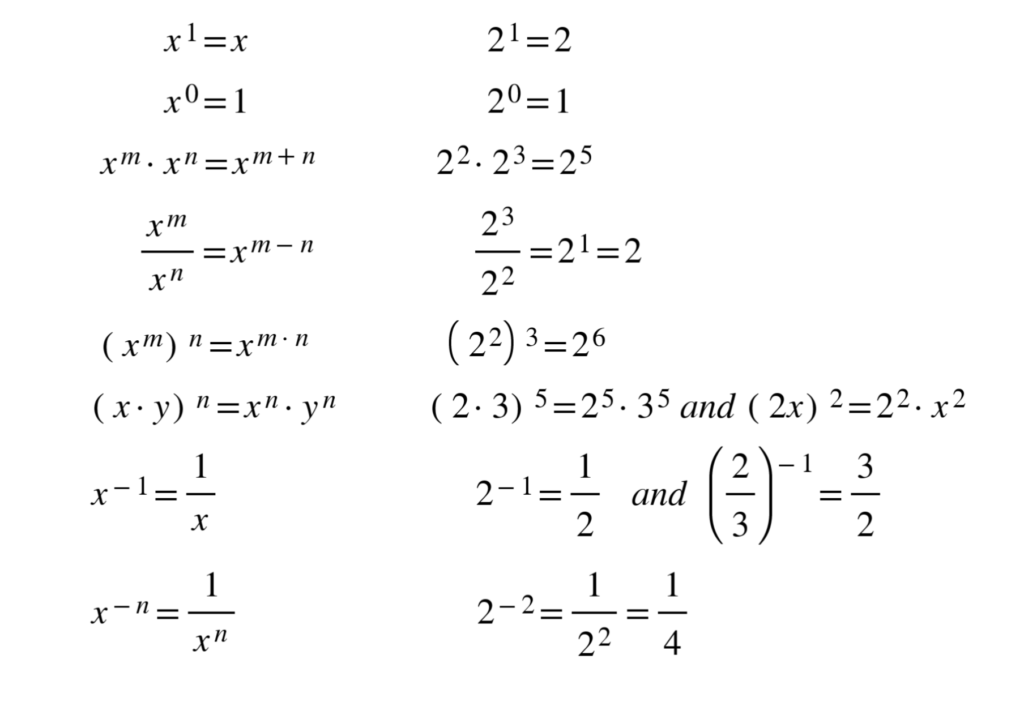
1.2.2 Fractional exponents
When doing mathematical operations (+, −, × or ÷) with fractions in the exponent you will need the following rules. These are often helpful when writing your answers in simplest terms.
Example:
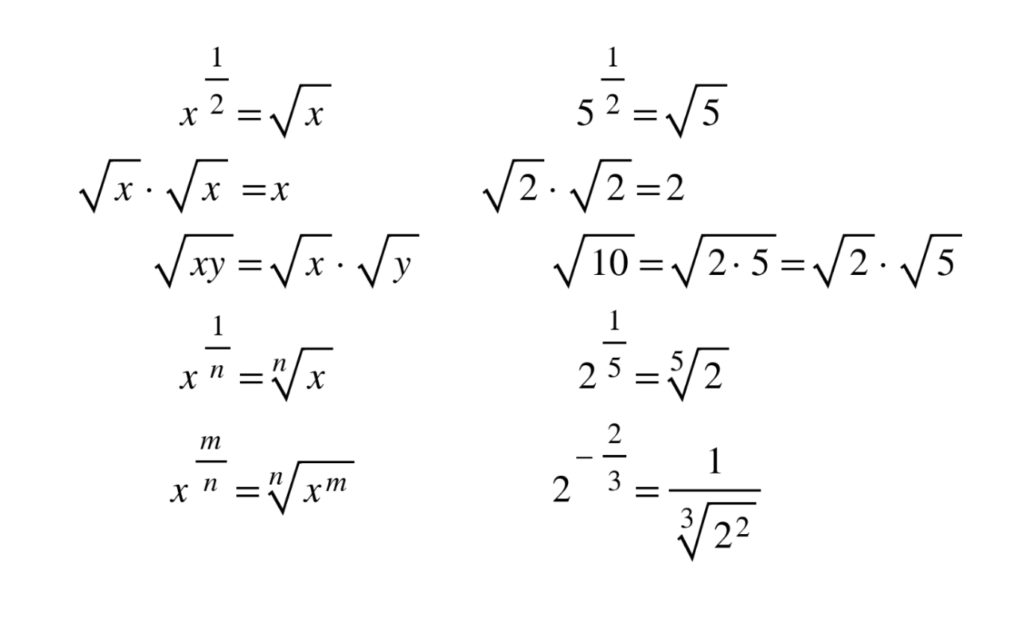
1.2.3 Laws of logarithms
Logarithms are the inverse mathematical operation of exponents, like division is the inverse mathematical operation of multiplication. The logarithm is often used to find the variable in an exponent.
DB 1.5 ax = b ⇔ x = Logab
Since loga ax = x, so then x = loga b.
This formula shows that the variable x in the power of the exponent becomes the subject of your log equation, while the number a becomes the base of your logarithm.
Logarithms with bases of 10 and e have special notations in which their base is not explicitly noted.
log10 x = log x
loge x = ln x
(Note: Remember that e is just the irrational number 2.71828…, so the same laws apply to ln as to other logarithms.)
Below are the rules that you will need to use when performing calculations with logarithms and when simplifying them. The sets of equations on the left and right are the same; on the right we show the notation that the formula booklet uses while the equations on the left are easier to understand.
Laws of logarithms and change of base
DB 1.7
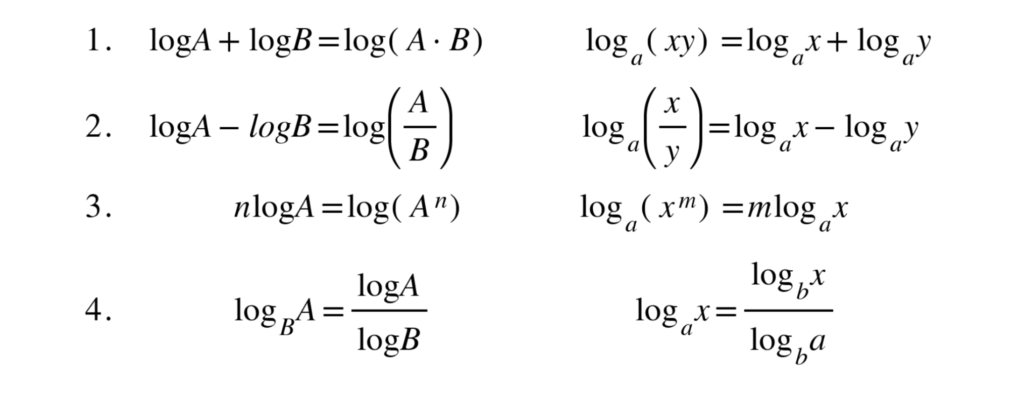
(Note: With the 4th rule you can change the base of a log)
Next to these rules, there are a few handy things to keep in mind when working with logarithms.
loga 0 = x is always undefined (because ax ≠ 0)
x = loga a = 1, which also means that ln e = 1
elna = a
Solve for x in the exponent using logarithms
Solve 2x = 13
- Take the log on both sides
2. Use rule III to take x outside
x log 2 = log 13
3. Solve
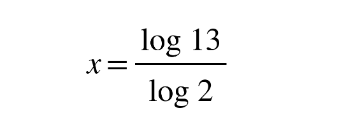
Expressing logs in terms of other logs
Example: Given that p = loga 5 and q = loga 2 express the following in terms of p and q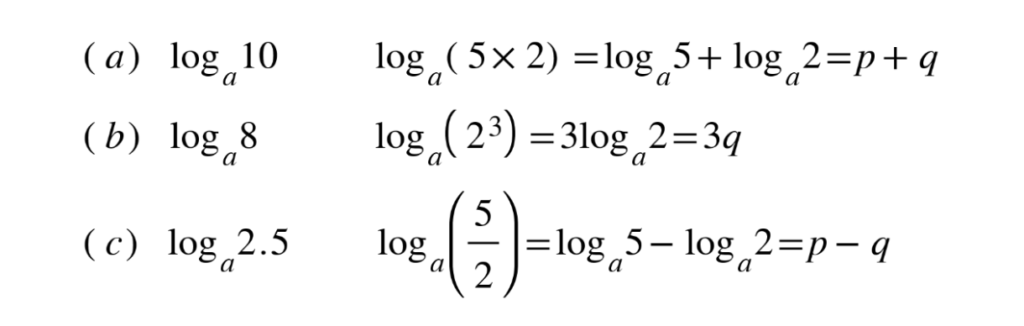
Exponents and Logarithms FAQs
Exponents and logarithms are **inverse operations** of each other, just like addition is the inverse of subtraction, or multiplication is the inverse of division.
An **exponent** asks "What is the result of multiplying a base number by itself a certain number of times?". For example, in \(2^3 = 8\), the base is 2, the exponent is 3, and the result is 8. It asks "2 multiplied by itself 3 times is what?".
A **logarithm** asks "What exponent do you need to raise a specific base number to, in order to get another number?". For example, the logarithmic form of \(2^3 = 8\) is \(\log_2(8) = 3\). This reads "log base 2 of 8 equals 3". It asks "What exponent do you need to raise 2 to, to get 8? The answer is 3."
They express the same relationship between three numbers, just from different perspectives.
True. A logarithm *is* the exponent to which a given base must be raised to produce a certain number.
In the statement \(\log_b(x) = y\), the value \(y\) (the logarithm) is the exponent you put on the base \(b\) to get \(x\). This is equivalent to the exponential statement \(b^y = x\).
The core meaning of a logarithm is simply finding that missing exponent.
Yes, logarithms and exponentiation (raising a base to a power) with the same base are **inverse operations**. This means one operation 'undoes' the other.
- If you start with a number \(x\), raise a base \(b\) to the power of \(x\) (\(b^x\)), and then take the logarithm base \(b\) of the result, you get back \(x\): \(\log_b(b^x) = x\).
- If you start with a number \(y\), take the logarithm base \(b\) of \(y\) (\(\log_b(y)\)), and then raise the base \(b\) to that result, you get back \(y\): \(b^{\log_b(y)} = y\) (for \(y > 0\)).
This inverse property is fundamental to solving exponential equations using logarithms and vice-versa.
The conversion is based directly on their inverse relationship:
The equation \(\log_b(x) = y\) is equivalent to \(b^y = x\).
- To convert from logarithmic to exponential form: Identify the base (\(b\)), the logarithm (which is the exponent, \(y\)), and the result (\(x\)). Then write it as baseexponent = result.
- To convert from exponential to logarithmic form: Identify the base (\(b\)), the exponent (\(y\)), and the result (\(x\)). Then write it as \(\log_{base}(result) = exponent\).
Example: \(\log_{10}(100) = 2\) converts to \(10^2 = 100\). Example: \(5^3 = 125\) converts to \(\log_5(125) = 3\).
One of the most useful properties of logarithms directly involves exponents: **The Power Rule**.
It states: \(\log_b(x^p) = p \cdot \log_b(x)\)
This means the exponent inside a logarithm can be moved to the front as a multiplier. This property is key for simplifying expressions and solving equations where the variable is in the exponent.
Example: \(\log_2(8^5) = 5 \cdot \log_2(8) = 5 \cdot 3 = 15\).
To expand a logarithm of a term raised to an exponent, you use this rule to bring the exponent out front.
The properties of logarithms are derived directly from the properties of exponents due to their inverse relationship:
- Product Rule: Exponents: \(b^m \cdot b^n = b^{m+n}\). Logarithms: \(\log_b(xy) = \log_b(x) + \log_b(y)\) (Multiplication inside log becomes addition outside).
- Quotient Rule: Exponents: \(b^m / b^n = b^{m-n}\). Logarithms: \(\log_b(x/y) = \log_b(x) - \log_b(y)\) (Division inside log becomes subtraction outside).
- Power Rule: Exponents: \((b^m)^n = b^{mn}\). Logarithms: \(\log_b(x^p) = p \cdot \log_b(x)\) (Exponent inside log becomes multiplication outside).
These parallels highlight how logarithms translate multiplicative relationships into additive ones, making complex calculations (historically, before calculators) much simpler.
Solving these equations often involves using the inverse relationship to switch between forms:
- To solve an exponential equation (variable in the exponent, e.g., \(b^x = k\)): Take the logarithm of both sides (often using log base \(b\), or the natural log ln). This uses the property \(\log_b(b^x) = x\) to isolate the variable.
- To solve a logarithmic equation (variable inside the log, e.g., \(\log_b(x) = y\)): Convert the equation to exponential form \(b^y = x\) to isolate the variable.
You also use the properties (product, quotient, power) to simplify expressions before converting forms or isolating variables.
Yes, exponential and logarithmic functions are fundamental concepts in calculus. You study their limits, derivatives, and integrals. The derivatives of \(e^x\) and \(\ln(x)\) are particularly important and have unique properties that make them central to many calculus applications.
