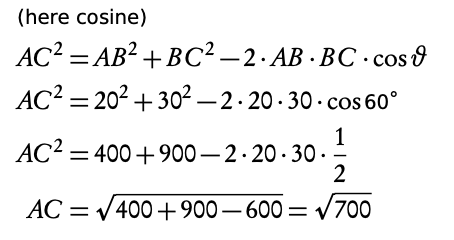📐 Basic Trigonometry Study Notes
Complete Guide for IB Mathematics
Comprehensive Theory & Interactive Practice
📌 Introduction to Trigonometry
Trigonometry is the branch of mathematics that studies relationships between the sides and angles of triangles. The word comes from Greek: "trigonon" (triangle) + "metron" (measure).
In IB Mathematics, trigonometry forms a fundamental topic appearing in both Analysis & Approaches (AA) and Applications & Interpretation (AI) courses at SL and HL levels.
🎯 Why Trigonometry is Essential in IB
- Foundation Topic: Core concept required for calculus, vectors, complex numbers, and physics applications
- Exam Weight: Typically 15-20% of total exam marks across Papers 1 and 2
- Real-World Applications: Engineering, architecture, navigation, physics, computer graphics, and signal processing
- Cross-Curricular: Essential for IB Physics (waves, forces, projectile motion) and Design Technology
- Higher Mathematics: Foundation for differential calculus, integration, and advanced analysis
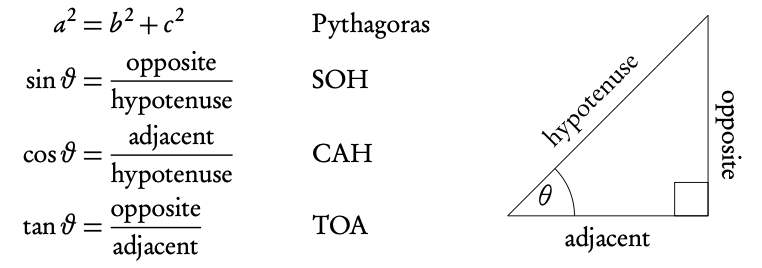
📊 Trigonometric Ratios - SOHCAHTOA
In a right-angled triangle, the six trigonometric ratios relate the angles to the side lengths. The three primary ratios are:
Sine (sin)
The ratio of the side opposite to angle θ to the hypotenuse
Cosine (cos)
The ratio of the side adjacent to angle θ to the hypotenuse
Tangent (tan)
The ratio of the opposite side to the adjacent side
Alternative Definition
Tangent can also be expressed using sine and cosine
Reciprocal Trigonometric Ratios
Three additional ratios are the reciprocals of the primary ratios:
Cosecant (csc)
Secant (sec)
Cotangent (cot)
Alternative Form
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
📝 Worked Example 1
In a right-angled triangle, the hypotenuse is 10 cm, and the side opposite to angle θ is 6 cm. Find sin(θ), cos(θ), and tan(θ).
sin(θ) = Opposite / Hypotenuse = 6 / 10 = 0.6 or 3/5
a² + b² = c²
Adjacent² + 6² = 10²
Adjacent² = 100 - 36 = 64
Adjacent = 8 cm
cos(θ) = Adjacent / Hypotenuse = 8 / 10 = 0.8 or 4/5
tan(θ) = Opposite / Adjacent = 6 / 8 = 0.75 or 3/4
Or: tan(θ) = sin(θ) / cos(θ) = 0.6 / 0.8 = 0.75 ✓
⭕ Unit Circle & Standard Angles
The unit circle is a circle with radius 1 centered at the origin (0, 0) of the coordinate plane. It extends trigonometry beyond right triangles to all angles.
For any angle θ measured from the positive x-axis:
cos(θ) = x-coordinate and sin(θ) = y-coordinate
Degrees and Radians
Angles can be measured in degrees or radians. In IB Mathematics, radians are preferred for calculus applications.
Conversion Formulas
Conversion Rules
Multiply by π/180
Multiply by 180/π
Standard Angle Values
These exact values must be memorized for IB exams (not provided in formula booklet):
| Angle (Degrees) | Angle (Radians) | sin(θ) | cos(θ) | tan(θ) |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 or √3/3 |
| 45° | π/4 | √2/2 or 1/√2 | √2/2 or 1/√2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 |
| 90° | π/2 | 1 | 0 | undefined |
| 180° | π | 0 | -1 | 0 |
| 270° | 3π/2 | -1 | 0 | undefined |
| 360° | 2π | 0 | 1 | 0 |
For sin: √0/2, √1/2, √2/2, √3/2, √4/2 → Simplify to: 0, 1/2, √2/2, √3/2, 1
For cos: Reverse the sin values
For tan: sin/cos or use special triangles (30-60-90 and 45-45-90)
CAST Diagram (Sign Rules)
The CAST (or All Students Take Calculus) rule determines the sign of trigonometric ratios in each quadrant:
S (Sine +) Quadrant I
A (All +)
T (Tan +) Quadrant IV
C (Cos +)
Quadrant II (90° to 180°): Only sine (and cosecant) positive
Quadrant III (180° to 270°): Only tangent (and cotangent) positive
Quadrant IV (270° to 360°): Only cosine (and secant) positive
🔢 Pythagorean & Fundamental Identities
These identities are derived from the Pythagorean theorem and are essential for simplifying trigonometric expressions and solving equations.
The Three Pythagorean Identities
Derived Forms & Rearrangements
From sin²(θ) + cos²(θ) = 1, we can derive:
From 1 + tan²(θ) = sec²(θ), we can derive:
Quotient & Reciprocal Identities
Quotient Identities
Reciprocal Identities
📝 Worked Example 2
If sin(θ) = 3/5 and θ is in the first quadrant, find cos(θ) and tan(θ).
sin²(θ) + cos²(θ) = 1
(3/5)² + cos²(θ) = 1
9/25 + cos²(θ) = 1
cos²(θ) = 1 - 9/25 = 16/25
cos(θ) = ±4/5
Since θ is in Quadrant I (All positive), cos(θ) = +4/5
tan(θ) = sin(θ) / cos(θ) = (3/5) / (4/5) = 3/4 = 0.75
📈 Trigonometric Functions & Graphs
Understanding the graphs of trigonometric functions is crucial for solving equations and modeling periodic phenomena.
Key Properties of Trig Functions
| Function | Period | Domain | Range | Amplitude |
|---|---|---|---|---|
| y = sin(x) | 2π or 360° | All real numbers | [-1, 1] | 1 |
| y = cos(x) | 2π or 360° | All real numbers | [-1, 1] | 1 |
| y = tan(x) | π or 180° | x ≠ π/2 + nπ | All real numbers | N/A |
Transformations of Trig Functions
General form for transformed trigonometric functions:
Parameter A (Amplitude)
|A| = Amplitude (vertical stretch/compression)
If A < 0, graph is reflected over x-axis
Amplitude = |A|
Parameter B (Period)
Affects the period (horizontal stretch/compression)
Period = 2π/|B| (for sin and cos)
Period = π/|B| (for tan)
Parameter C (Phase Shift)
Horizontal shift = C
C > 0: shift right
C < 0: shift left
Parameter D (Vertical Shift)
Vertical shift = D
D > 0: shift up
D < 0: shift down
Also called the midline
📝 Worked Example 3
For the function y = 3sin(2(x - π/4)) + 1, identify the amplitude, period, phase shift, and vertical shift.
Comparing with y = A·sin(B(x - C)) + D:
A = 3, B = 2, C = π/4, D = 1
Amplitude = |A| = |3| = 3
Period = 2π/|B| = 2π/2 = π
Phase shift = C = π/4 to the right
Vertical shift = D = 1 unit up
⚙️ Solving Trigonometric Equations
Trigonometric equations require finding all angles that satisfy the equation within a given domain. Key strategies include:
Strategy 1: Isolate the Trig Function
Rearrange equation to get sin(θ), cos(θ), or tan(θ) alone on one side
Strategy 2: Find Principal Solution
Use calculator or unit circle to find the first solution (usually in [0°, 360°) or [0, 2π))
Strategy 3: Find All Solutions
Use CAST diagram and symmetry to find additional solutions in the given domain
Strategy 4: Check Domain
Verify all solutions fall within the specified interval
Finding Multiple Solutions
For equations in the form sin(θ) = k, cos(θ) = k, or tan(θ) = k:
For sin(θ) = k
If θ₁ is one solution, the second solution in [0°, 360°] is:
θ₂ = 180° - θ₁ (or θ₂ = π - θ₁ in radians)
For cos(θ) = k
If θ₁ is one solution, the second solution in [0°, 360°] is:
θ₂ = 360° - θ₁ (or θ₂ = 2π - θ₁ in radians)
For tan(θ) = k
If θ₁ is one solution, the second solution in [0°, 360°] is:
θ₂ = 180° + θ₁ (or θ₂ = π + θ₁ in radians)
📝 Worked Example 4
Solve 2sin(θ) - 1 = 0 for 0° ≤ θ ≤ 360°.
2sin(θ) = 1
sin(θ) = 1/2
From standard angles: sin(30°) = 1/2
So θ₁ = 30°
For sine, second solution: θ₂ = 180° - 30° = 150°
30° is in Q1 (All positive) ✓
150° is in Q2 (Sine positive) ✓
📐 Sine Rule & Cosine Rule
For non-right-angled triangles, we use the Sine Rule and Cosine Rule to find unknown sides and angles.
The Sine Rule
Alternative form (useful for finding angles):
Use Sine Rule when:
• You know two angles and one side (AAS or ASA)
• You know two sides and a non-included angle (SSA - ambiguous case)
The Cosine Rule
Finding a Side
Finding an Angle
Use Cosine Rule when:
• You know three sides and need to find an angle (SSS)
• You know two sides and the included angle (SAS)
Area Formula for Triangles
When you know two sides and the included angle:
📝 Worked Example 5
In triangle ABC, a = 8 cm, b = 10 cm, and angle C = 60°. Find side c.
We have two sides and the included angle (SAS)
Use Cosine Rule
c² = a² + b² - 2ab·cos(C)
c² = 8² + 10² - 2(8)(10)cos(60°)
c² = 64 + 100 - 160(0.5)
c² = 164 - 80
c² = 84
c = √84 = 9.17 cm (to 3 s.f.)
✍️ Interactive Practice Problems
Test your trigonometry knowledge with these IB-style problems!
Problem 1: Basic Ratios
Find sin(θ). Give your answer as a decimal to 3 d.p.
📖 Complete Solution
Problem 2: Unit Circle Values
Enter as a fraction: use / for division (e.g., 1/2)
📖 Complete Solution
Problem 3: Pythagorean Identity
Give your answer as a decimal to 2 d.p.
📖 Complete Solution
0.36 + cos²(θ) = 1
cos(θ) = ±0.8
Problem 4: Solving Trig Equations
Enter both solutions separated by a comma (e.g., 30,150)
📖 Complete Solution
From standard angles: cos(120°) = -1/2 = -0.5
Problem 5: Amplitude and Period
Enter just the number.
📖 Complete Solution
Where A is the amplitude coefficient
A = 4, B = 3
⚠️ Common Mistakes to Avoid
❌ Mistake 1: Confusing Opposite & Adjacent
Always identify sides relative to the angle in question
Draw and label the triangle clearly first
❌ Mistake 2: Calculator Mode
Using degrees when answer requires radians (or vice versa)
Always check calculator is in correct mode (DEG or RAD)
❌ Mistake 3: Missing Solutions
Finding only one solution when two exist
Use CAST diagram and symmetry to find all solutions
❌ Mistake 4: Sign Errors
Forgetting that trig ratios can be negative
Remember CAST rule for signs in each quadrant
❌ Mistake 5: Wrong Rule Selection
Using sine rule when cosine rule is needed
SSS or SAS → Cosine Rule; AAS or ASA → Sine Rule
❌ Mistake 6: Rounding Too Early
Rounding intermediate steps causes accumulation errors
Keep full calculator display until final answer
🎓 IB Exam Tips & Strategy
📝 Essential Exam Techniques
- Formula Booklet: IB provides some trig formulas but NOT standard angle values - memorize 0°, 30°, 45°, 60°, 90°
- Show Working: Even if using GDC, write out formula and substitution for method marks
- Exact Values: When question says "exact," give answers as fractions/surds, not decimals
- Units: Always check if answer should be in degrees or radians - marks lost for wrong units
- Diagram Sketching: For word problems, always draw and label a diagram first
- GDC Verification: Use calculator to check answers, especially for solving equations
- Domain Awareness: Read carefully - is domain [0°, 360°], [0°, 180°], or [-180°, 180°]?
⏰ Time Management
- Basic Trig Ratio Questions: 2-3 minutes (typically 2-3 marks)
- Unit Circle Values: 1-2 minutes (should be instant recall)
- Solving Equations: 4-5 minutes (typically 4-6 marks)
- Sine/Cosine Rule: 5-7 minutes (typically 5-8 marks)
- Graph Transformations: 3-4 minutes per part
📌 Quick Reference Summary
- SOHCAHTOA: sin = O/H, cos = A/H, tan = O/A
- Pythagorean Identity: sin²θ + cos²θ = 1
- Period: sin & cos: 2π (360°); tan: π (180°)
- Key Angles: 0°, 30°, 45°, 60°, 90° (memorize exact values!)
- CAST Rule: Q1-All, Q2-Sine, Q3-Tan, Q4-Cos (positive)
- Sine Rule: a/sin(A) = b/sin(B) = c/sin(C)
- Cosine Rule: a² = b² + c² - 2bc·cos(A)
- Area: (1/2)ab·sin(C)
📐 Master trigonometry through understanding and practice!
Visit RevisionTown.com for comprehensive IB study resources
This section offers an overview of some basic trigonometry rules and values that will recur often. It is worthwhile to know these by heart; but it is much better to understand how to obtain these values. Like converting between Celsius and Fahrenheit; you can remember some values that correspond to each other but if you understand how to obtain them, you will be able to convert any temperature.
3.2.1 Converting between radians and degrees
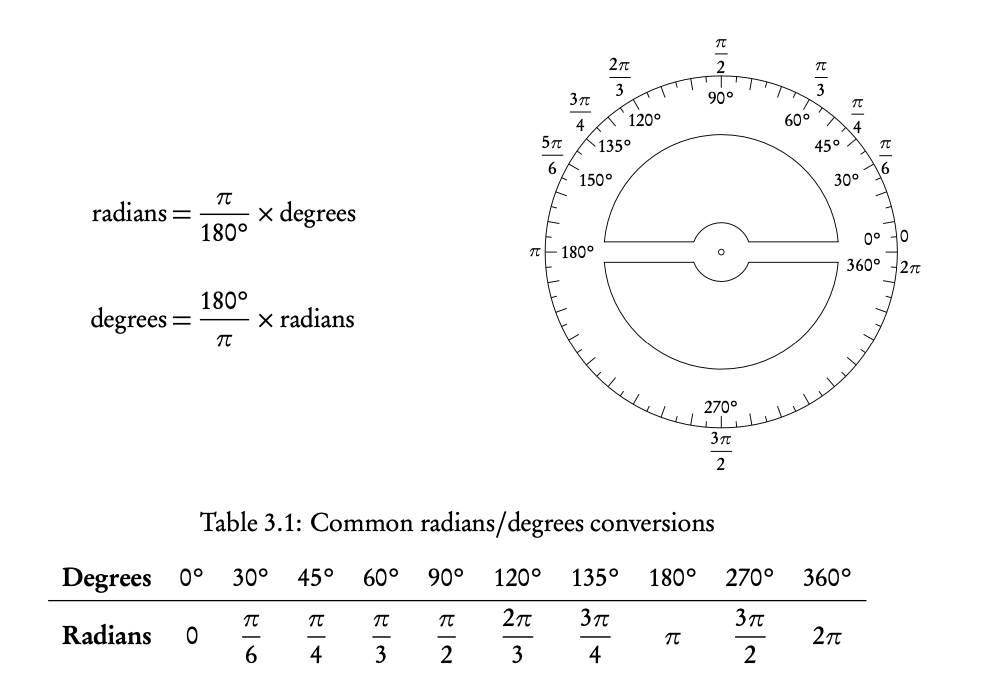
3.2.2 Circle formulas
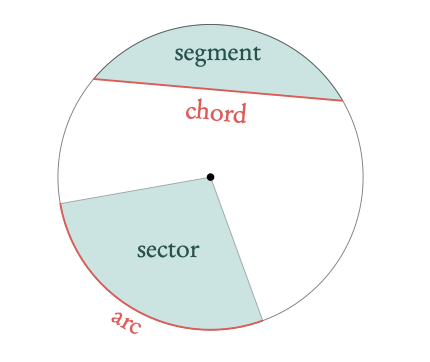
Area of a sector = ½ r2 · θ
Arc length = r · θ
θ in radians, r = radius.
DB. 3.4
3.2.3 Right-angle triangles
The following two right angle triangles with whole numbers for all the sides come up often in past exam questions.
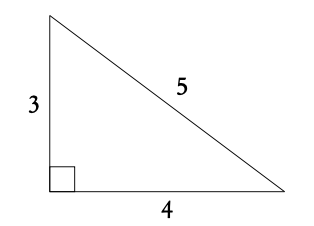
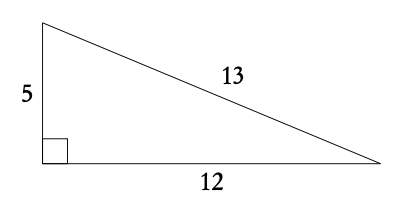
The two triangles below can help you in finding the sin, cos and tan of the angles that you should memorize, shown in table 3.2 on page 40. Use SOH, CAH, TOA to find the values.
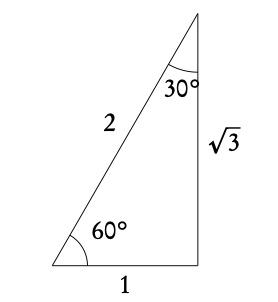
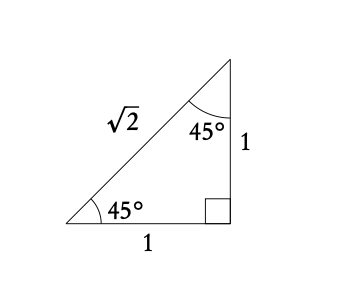
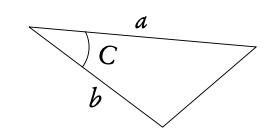
3.2.4 Non-right angle triangles
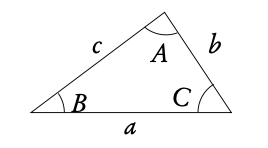
To find any missing angles or side lengths in non-right angle triangles, use the cosine and sine rule. Remember that the angles in the triangle add up to 180°!
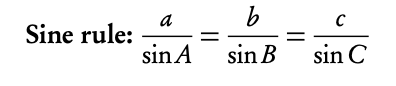
Use this rule when you know:
2 angles and a side
(not between the angles)
or
2 sides and an angle
(not between the sides)
Cosine rule: c2 =a2 + b2 − 2ab cosC
Use this rule when you know:
3 sides
or
2 sides and the angle between them
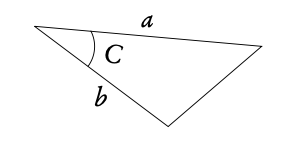
Area of a triangle: Area = ½ ab sinC
Use this rule when you know:
2 sides and the angle between them
DB 3.2
Read the question: does it specify if you are looking for an acute (less than 90°) or obtuse (more than 90°) angle? If not there may be 2 solutions. Exam hint: Use sketches when working with worded questions!
Example: △ABC: A = 40°, B = 73°, a = 27 cm.
Example:
3.2.5 Ambiguous case
Ambiguous case, also known as an angle-side-side case, is when the triangle is not unique from the given information. It happens when you are given two sides and an angle not between those sides in a triangle.
You have to use a sine rule to solve a problem in this case. However, one needs to remember that sin x = sin(180° − x ), meaning that your answer for an angle is not just x , but also 180° − x.
In other words, we might get two different possible angles as an answer and thus two different possible triangles that satisfy the information given.
However, that is not always the case, if the sum of the two known angles becomes bigger than 180°. So if you are required to calculate the third angle or total area of a triangle, you might have to do the calculations for two different triangles using both of your angles.
Example: △ABC : B = 33°, a = 23cm, b = 14cm. Find ∠A.
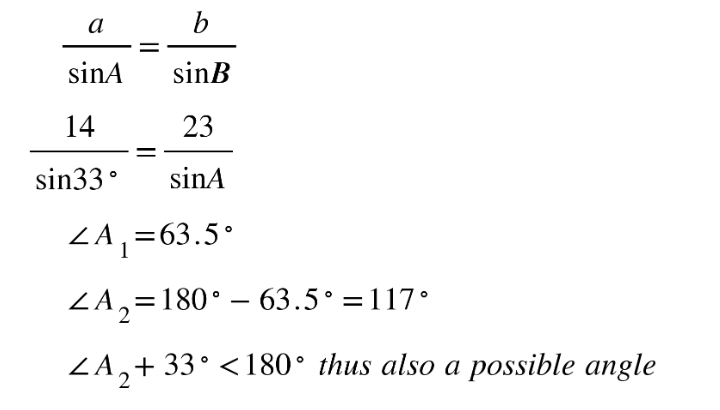
Draw the two possible triangles.
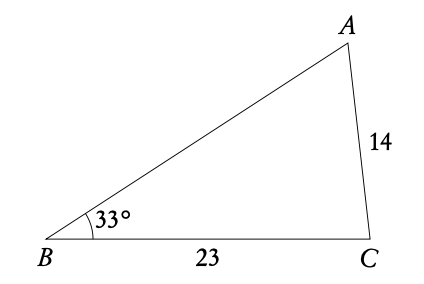
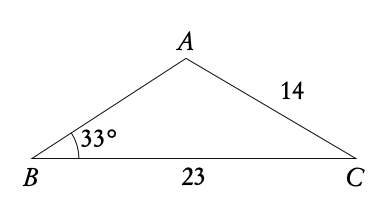
3.2.6 Three-figure bearings
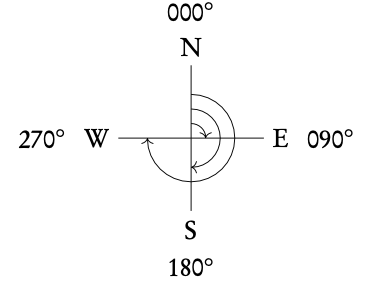
Three-figure bearings can be used to indicate compass directions on maps. They will be given as an angle of a full circle, so between 0° and 360°. North is always marked as 0°. Any direction from there can be expressed as the angle in the clockwise direction from North.
In questions on three-figure bearings, you are often confronted with quite a lot of text, so it is a good idea to first make a drawing. You may also need to create a right angle triangle and use your basic trigonometry.
Example:
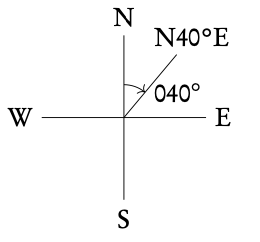
N40°E: 40° East of North = 40°
Solving questions with three-figure bearings
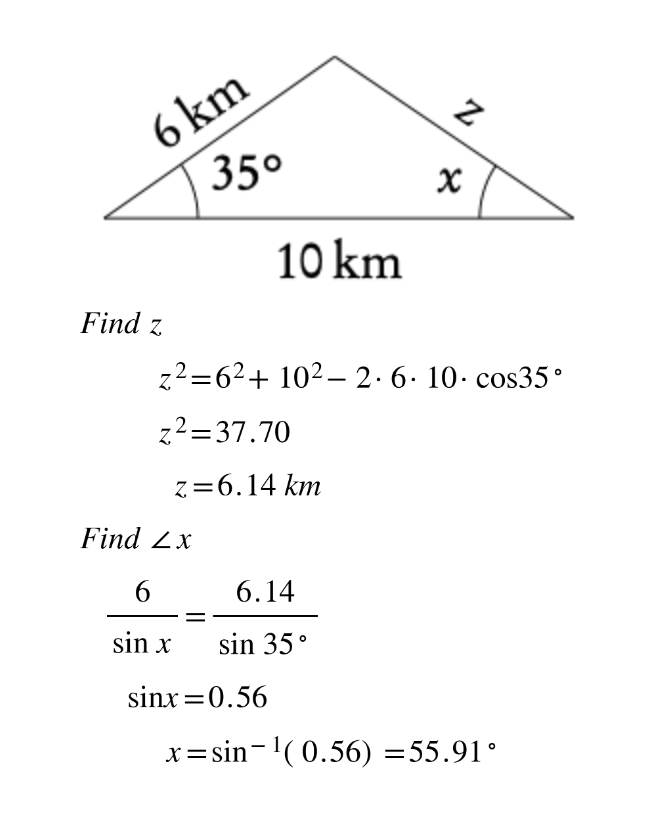
A ship left port A and sailed 20 km in the direction 120°. It then sailed north for 30 km to reach point C . How far from the port is the ship?
Sketch
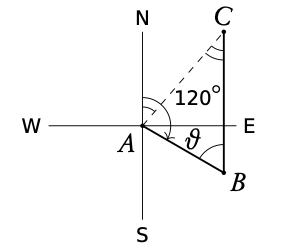
2. Find an internal angle of the triangle
θ = 180° − 120° = 60° = C
Similar angles between two parallel lines
3. Use cosine or sin rule
