⭕ Circular Functions Study Notes
Complete IB Mathematics Guide
Unit Circle • Trigonometric Identities • Graphs & Transformations
📌 Introduction to Circular Functions
Circular functions (also called trigonometric functions) are mathematical functions defined using angles and the unit circle. They relate angles to ratios and are fundamental in mathematics, physics, engineering, and many real-world applications.
Unlike right triangle trigonometry which is limited to angles between 0° and 90°, circular functions extend trigonometry to all real numbers, allowing us to work with any angle value, positive or negative.
🎯 Why Circular Functions in IB Mathematics?
- Core IB Topic: Essential component of IB Math AA and AI at both SL and HL levels
- Exam Significance: Typically 15-20% of Geometry & Trigonometry marks across papers
- Foundation for Calculus: Required for derivatives and integrals of trig functions
- Real-World Applications: Waves, oscillations, periodic phenomena, signal processing, engineering
- Technology Integration: Essential for computer graphics, animation, and game development
- Cross-Curricular: Used extensively in IB Physics (waves, SHM), Music, and Architecture
Angles: Degrees vs Radians
Angles can be measured in two systems: degrees and radians. IB Mathematics emphasizes radians.
Degrees → Radians
Example: 90° = 90 × (π/180) = π/2 radians
Radians → Degrees
Example: π/3 = (π/3) × (180/π) = 60°
⭕ The Unit Circle
The unit circle is a circle with radius 1 centered at the origin (0, 0) on the coordinate plane.
For any angle θ measured from the positive x-axis (counterclockwise):
Point on circle: (cos θ, sin θ)
Key Unit Circle Values (MUST MEMORIZE)
These exact values are NOT provided in the IB formula booklet. You must memorize them!
| Angle (Degrees) | Angle (Radians) | sin θ | cos θ | tan θ |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 or √3/3 |
| 45° | π/4 | √2/2 or 1/√2 | √2/2 or 1/√2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 |
| 90° | π/2 | 1 | 0 | undefined |
| 120° | 2π/3 | √3/2 | −1/2 | −√3 |
| 135° | 3π/4 | √2/2 | −√2/2 | −1 |
| 150° | 5π/6 | 1/2 | −√3/2 | −1/√3 |
| 180° | π | 0 | −1 | 0 |
| 270° | 3π/2 | −1 | 0 | undefined |
| 360° | 2π | 0 | 1 | 0 |
CAST Diagram (Sign Rules)
The CAST rule determines which functions are positive in each quadrant:
S (Sine +) Quadrant I
A (All +)
T (Tan +) Quadrant IV
C (Cos +)
📊 The Six Circular Functions
There are six fundamental circular functions, divided into primary and reciprocal functions:
Primary Functions
Reciprocal Functions
Cosecant (csc)
Reciprocal of sine
Undefined when sin θ = 0
Secant (sec)
Reciprocal of cosine
Undefined when cos θ = 0
Cotangent (cot)
Reciprocal of tangent
Undefined when sin θ = 0
📝 Worked Example 1
If sin θ = 3/5 and θ is in Quadrant II, find cos θ, tan θ, and sec θ.
sin²θ + cos²θ = 1
(3/5)² + cos²θ = 1
9/25 + cos²θ = 1
cos²θ = 16/25
cos θ = ±4/5
In Quadrant II, cosine is negative
cos θ = −4/5
tan θ = sin θ / cos θ
tan θ = (3/5) / (−4/5)
tan θ = −3/4
sec θ = 1 / cos θ
sec θ = 1 / (−4/5)
sec θ = −5/4
🔢 Pythagorean & Fundamental Identities
Three Pythagorean Identities
These can be rearranged into various useful forms:
From sin²θ + cos²θ = 1:
From 1 + tan²θ = sec²θ:
Quotient & Reciprocal Identities
Quotient Identities
Reciprocal Identities
📝 Worked Example 2: Proving an Identity
Prove: (1 − cos²θ) / sin θ = sin θ
LHS = (1 − cos²θ) / sin θ
Since sin²θ + cos²θ = 1, we have 1 − cos²θ = sin²θ
LHS = sin²θ / sin θ
LHS = sin²θ / sin θ = sin θ
LHS = RHS ✓
📈 Graphs of Circular Functions & Transformations
The general form for transformed circular functions is:
or
y = A·cos(B(x − C)) + D
Where each parameter controls a specific transformation:
Transformation Parameters
A = Amplitude
Vertical stretch/compression
Height from center line to peak
If A < 0: reflection over x-axis
B = Frequency/Period
Horizontal stretch/compression
Length of one complete cycle
Larger B = shorter period = more cycles
C = Phase Shift
Horizontal translation
C > 0: shift RIGHT
C < 0: shift LEFT
D = Vertical Shift
Vertical translation
D > 0: shift UP
D < 0: shift DOWN
Basic Function Properties
| Function | Period | Domain | Range |
|---|---|---|---|
| y = sin x | 2π | All real numbers | [−1, 1] |
| y = cos x | 2π | All real numbers | [−1, 1] |
| y = tan x | π | x ≠ π/2 + nπ | All real numbers |
📝 Worked Example 3: Identify Transformations
For y = 3sin(2(x − π/4)) + 1, find amplitude, period, phase shift, and vertical shift.
y = A·sin(B(x − C)) + D
A = 3, B = 2, C = π/4, D = 1
Amplitude = |A| = |3| = 3
Period = 2π / |B| = 2π / 2 = π
Phase shift = C = π/4 to the RIGHT
Vertical shift = D = 1 unit UP
Midline: y = 1
Maximum = D + |A| = 1 + 3 = 4
Minimum = D − |A| = 1 − 3 = −2
✍️ Interactive Practice Problems
Test your understanding with these IB-style circular functions problems!
Question 1: Unit Circle Values
Enter as a fraction with square root (e.g., sqrt(3)/2)
📖 Complete Solution
Question 2: Pythagorean Identity
Enter as a fraction (e.g., 3/5)
📖 Complete Solution
sin²θ + 16/25 = 1
sin²θ = 9/25
Answer: sin θ = 3/5
Question 3: Amplitude Identification
Enter as a positive number.
📖 Complete Solution
Question 4: Period Calculation
Enter in terms of π (e.g., pi/2 for π/2)
📖 Complete Solution
Question 5: Phase Shift
Enter: "left" or "right" followed by the amount (e.g., "right pi/6")
📖 Complete Solution
⚠️ Common Mistakes to Avoid
❌ Mistake 1: Calculator Mode
Using degrees when answer requires radians
✓ Check: Always use RADIAN mode for IB calculus questions
❌ Mistake 2: Sign Errors
Forgetting CAST rule for quadrants
✓ Check: Determine sign based on quadrant location
❌ Mistake 3: Period Formula
Using 2π/B for tan (should be π/B)
✓ Check: Tan has period π, sin/cos have period 2π
❌ Mistake 4: Amplitude Sign
Writing amplitude as negative
✓ Check: Amplitude = |A|, always positive
❌ Mistake 5: Phase Shift Direction
Confusing (x − C) and (x + C) direction
✓ Check: (x − C) = shift RIGHT, (x + C) = shift LEFT
❌ Mistake 6: Exact vs Decimal
Giving decimal when exact value required
✓ Check: Use √3/2, not 0.866 for exact values
🎓 IB Exam Tips & Strategy
📝 Essential Exam Techniques
- Memorize Unit Circle: Exact values for 0°, 30°, 45°, 60°, 90° (and their equivalents in other quadrants) are NOT in formula booklet
- Show Working: Write each step even if obvious - method marks available even with wrong final answer
- Use CAST Diagram: Sketch quickly to determine signs in different quadrants
- Check Calculator Mode: RADIAN mode for calculus, check before each question
- Exact vs Approximate: Use exact values (fractions, surds) unless question asks for decimal approximation
- Domain Restrictions: Note when functions are undefined (tan at π/2, sec at π/2, etc.)
- Prove Identity Strategy: Start with more complex side, use known identities, work toward simpler side
⏰ Time Management
- Unit Circle Values: 1-2 minutes (should be instant recall)
- Pythagorean Identity Problems: 3-4 minutes
- Identity Proofs: 5-7 minutes (show all steps)
- Graph Transformations: 4-5 minutes per question
- Sketching Graphs: 6-8 minutes (label key points)
📌 Quick Reference Summary
Essential Formulas
CAST Rule: All Students Take Calculus
Q1: All positive | Q2: Sin positive | Q3: Tan positive | Q4: Cos positive
👨🏫 About the Author
Adam
Co-Founder @ RevisionTown
Math Expert in Various Curricula: IB, AP, GCSE, IGCSE, A-Levels
Dedicated to helping students master circular functions and trigonometry. Specializing in IB Mathematics with focus on conceptual understanding, exam strategies, and real-world applications.
⭕ Master circular functions and excel in IB Mathematics!
Visit RevisionTown.com for more IB resources
3.3.1 Unit circle
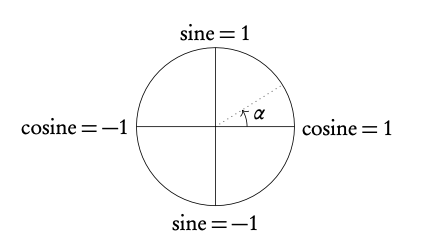
The unit circle is a circle with a radius of 1 drawn from the origin of a set of axes. The y-axis corresponds to sine and the x -axis to cosine; so at the coordinate (0, 1) it can be said that cosine = 0 and sine = 1, just like in the sin x and cos x graphs when plotted.
The unit circle is a a tool that you can use when solving problems involving circular functions. You can use it to find all the solutions to a trigonometric equation within a certain domain.
As you can see from their graphs, functions with sin x , cos x or tan x repeat themselves every given period; this is why they are also called circular functions. As a result, for each y-value there is an infinite amount of x-values that could give you the same output. This is why questions will give you a set domain that limits the x-values you should consider in your calculations or represent on your sketch (e.g. 0° ≤ x ≤ 360°).
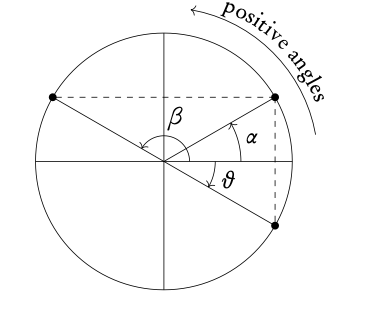
Relations between sin, cos and tan:
- α and β have the same sine
- α and θ have the same cosine
- β and θ have the same tangent
Example:
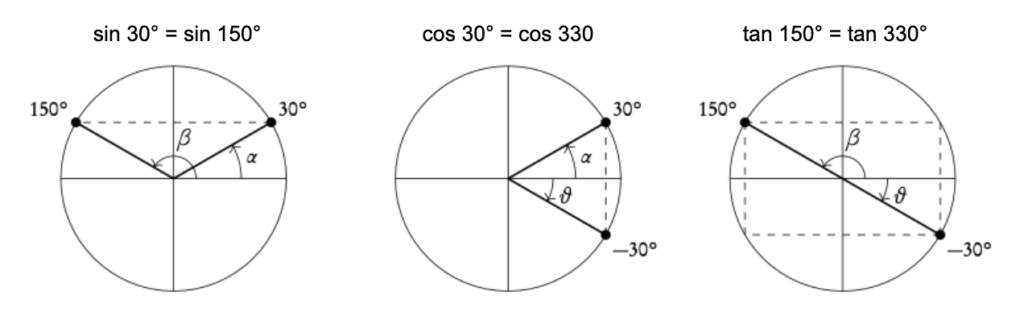
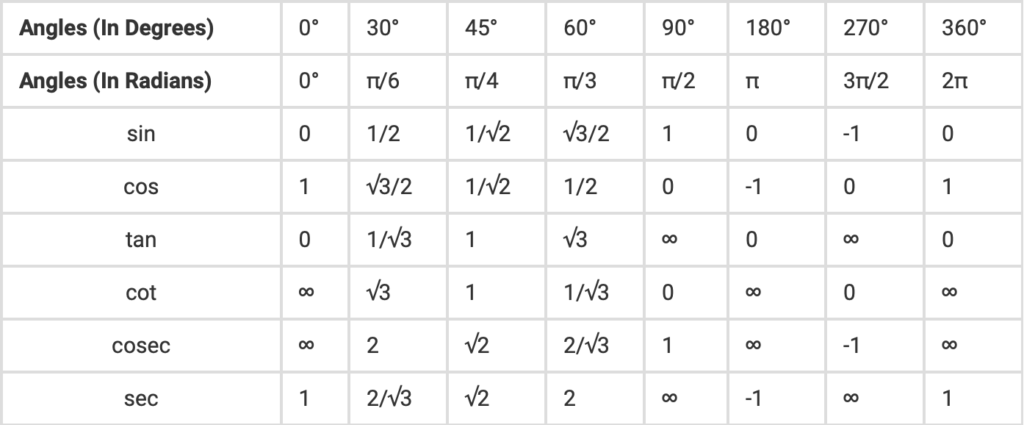
Table 3.2: Angles to memorize
3.3.2 Graphs of trigonometric functions
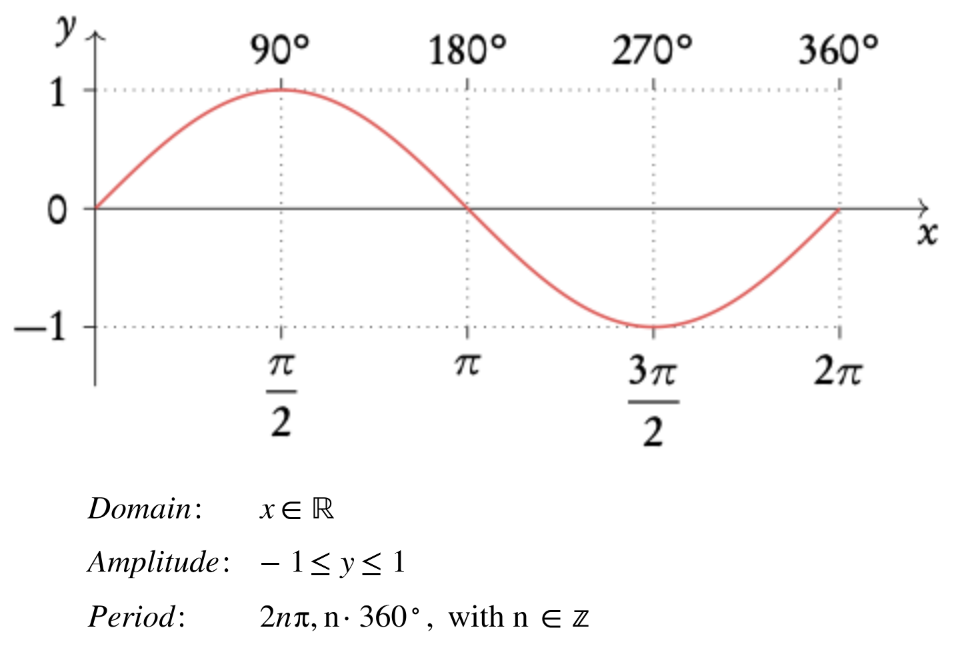
sin x
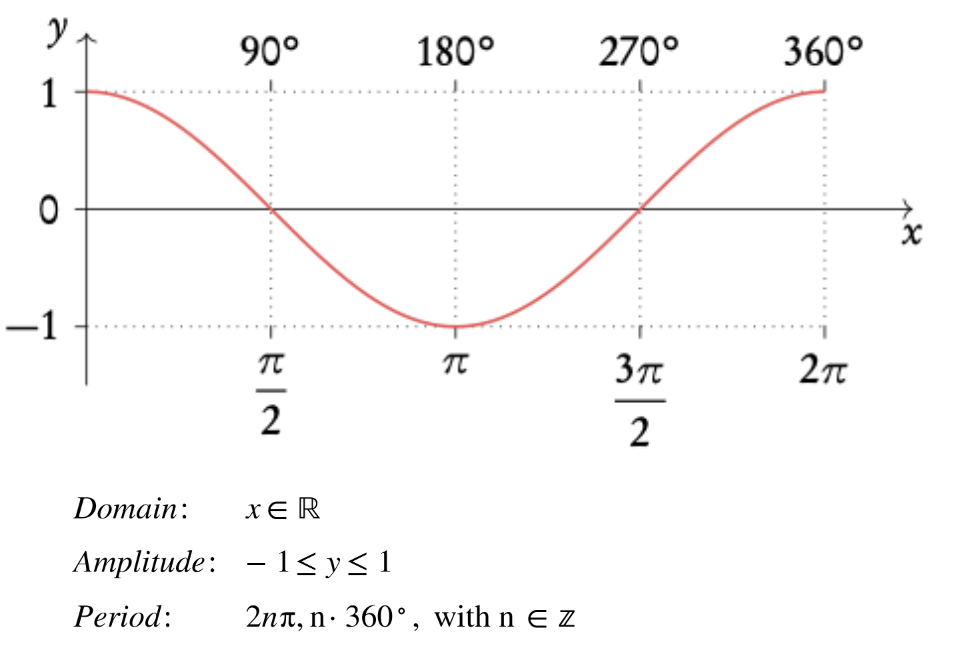
cos x
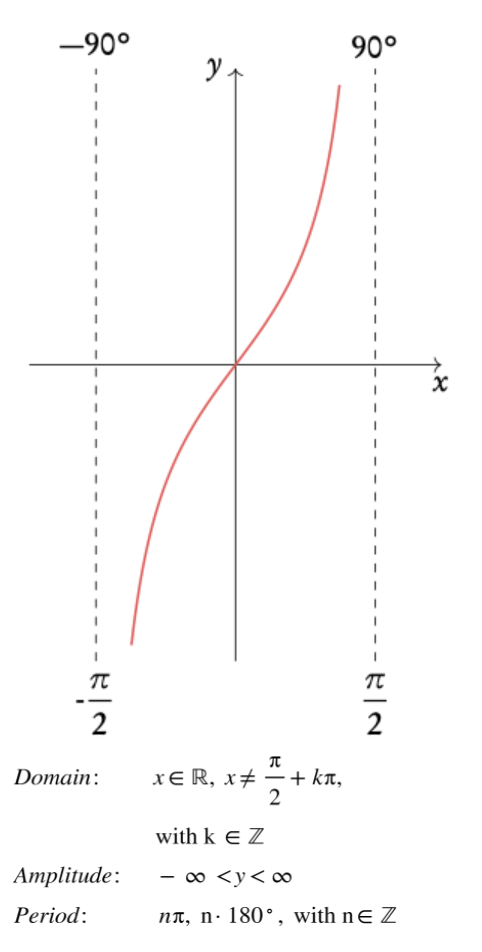
tan x
3.3.3 Transformations
Besides the transformations in the functions chapter, trigonometric functions have some transformations with their own particular names. For a trigonometric function, the vertical stretch on a graph is determined by its amplitude, the horizontal stretch by its period and an upward/downward shift by its axis of oscillation.
A trigonometric function, given by y = a sin(bx + c) + d, has:
- amplitude a
- period of 360°/b or 2π/b
- horizontal shift of +c to the left, in degrees or radians
- vertical shift of +d upwards, oscillates around d.
Note: A negative a will flip your graph around the x-axis. Negative values of c and d will lead to shifts to the right and downwards the respective number of units
Example: Transformations of y = cos x .
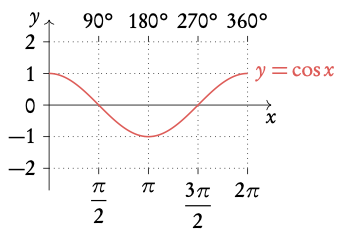
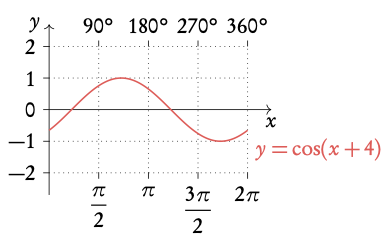
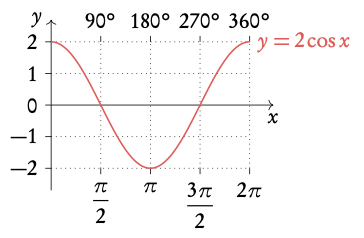
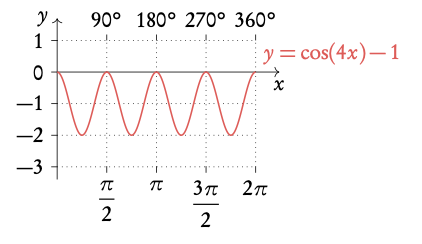
3.3.4 Identities and equations
In order to solve trigonometric equations, you will sometimes need to use identities. Identities allow you to rewrite your equation in a way that will make it easier to solve algebraically.
DB 3.5 & 3.6
Trigonometric identity
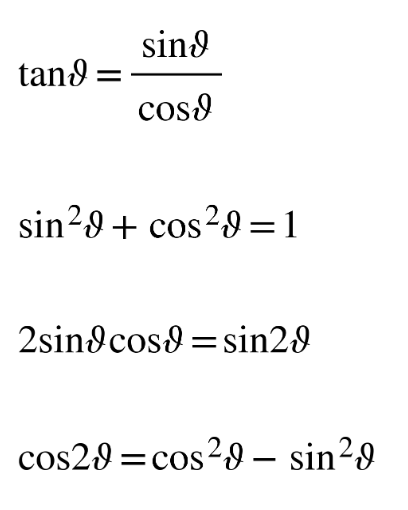
Popular rearrangement
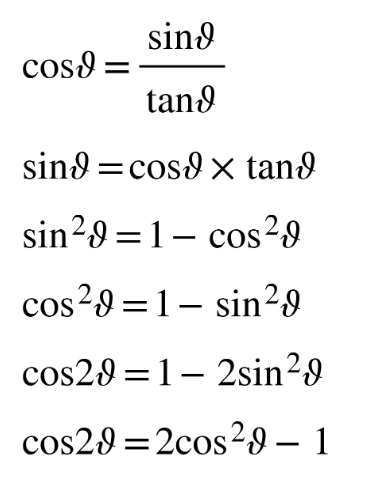
Solving equations with trigonometric identities
Solve 2cos2 x + sin x = 1, 0° ≤ x ≤ 360°.
- Identify which identity from the formula booklet to use. Note that you are always aiming to get an equation with just, sin, cos or tan.
Here we could use either
sin2 θ + cos2 θ = 1 or
cos2 θ − sin2 θ = cos 2θ.
We will use the first so that we get an equation with just sin.
2. Rearrange identity and substitute into equation.
cos2 θ = 1 − sin2 θ
2(1−sin2 x) + sinx = 1
2 − 2 sin2 x + sin x = 1
−2 sin2 x + sin x + 1 = 0
3. Solve for x giving answers within the stated range. Recognise that here the equation looks like a quadratic equation.
Substitute u for sinx:
−2u2 + u + 1 = 0
(−2u − 1)(u − 1) = 0
u = sinx ⇒ 1 x ⇒ 90°
u = sinx ⇒ −0.5 x ⇒ 210° or 330°