If we have two unknowns, for example x and y, and two equations, then we can solve for x and y simultaneously.
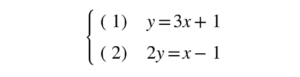
There are 3 methods to solve simultaneous equations.
Elimination
Multiply an equation and then subtract it from the other in order to eliminate one of the unknowns.
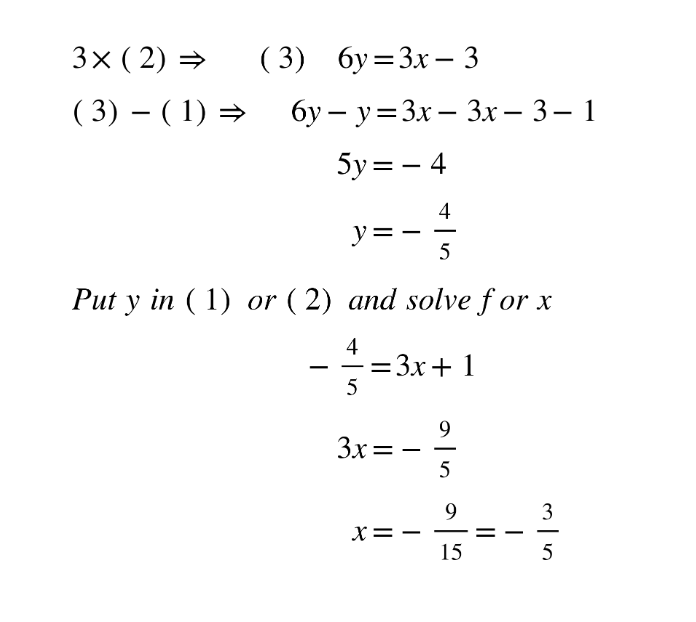
Substitution
Rearrange and then substitute one in to another.
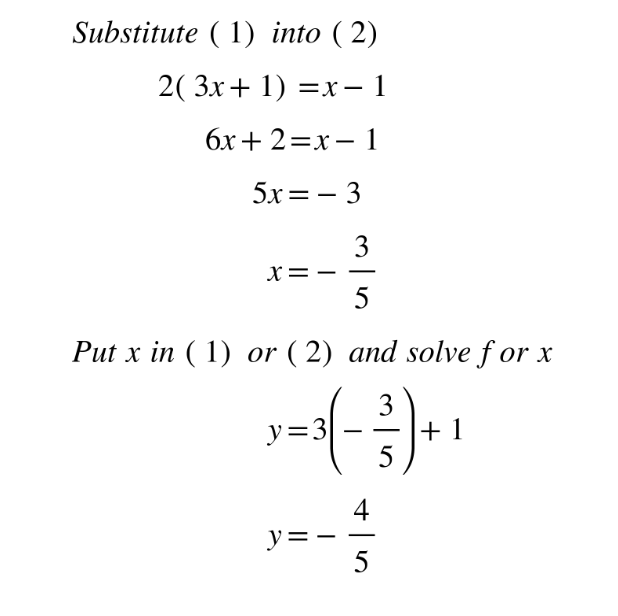
Graph
Graph both lines on your GDC. Where they intersect will be the solution to the equation.
Note that this method is also great when you have to solve more complex equations.
