Rearranging functions

2.2.1 Inverse functions, f −1(x)

Inverse functions are the reverse of a function. Finding the input x for the output y. You can think of it as going backwards through the number machine.

Inverse functions

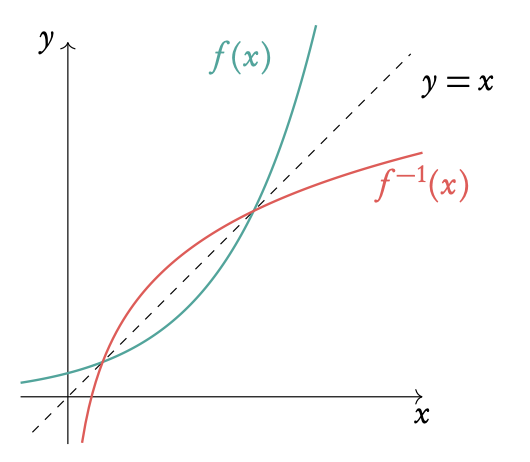
This is the same as reflecting a graph in the y = x axis.

Inverse functions 1

Finding the inverse function.

   f(x) = 2x3 + 3, find f −1(x)

  1. Replace f(x) with y

     y = 2x3 + 3

2. Solve for x

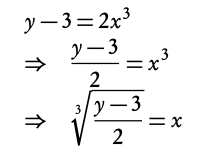
Inverse functions 2
3. Replace x with f −1(x) and y with x
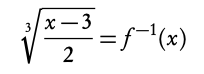
Inverse functions 3

2.2.2 Composite functions

   Composite functions are a combination of two functions.

   (f ◦ g)(x) means f of g of x

To find the composite function above substitute the function of g(x) into the x of f (x).

Example: Let f(x) = 2x + 3 and g(x) = x2. Find (f ◦ g)(x) and (g ◦ f )(x).

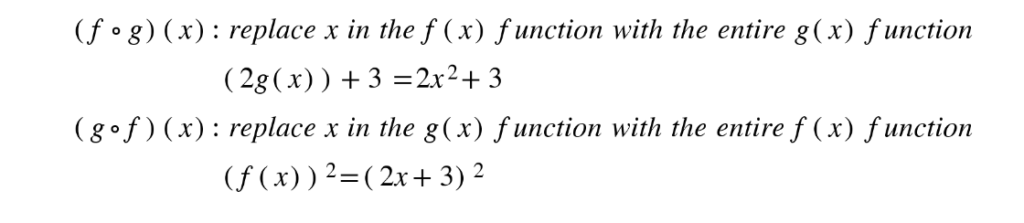
Composite functions

Note: Remember f ◦ g(x) ≠ g ◦ f(x)

2.2.3 Transforming functions

By adding and/or multiplying by constants we can transform a function into another function.

Transforming functions

Exam hint: describe the transformation with words as well to guarantee marks. 

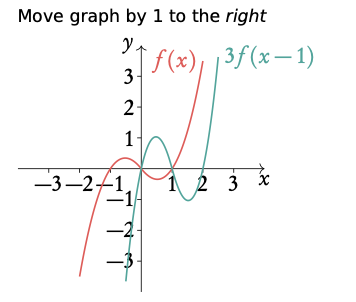
Always do translations last

Transforming functions f (x) → af (x + b)

Given f(x)=¼ x3 + x2 − 5/4 x, draw 3f (x−1).

  1. Sketch f(x)
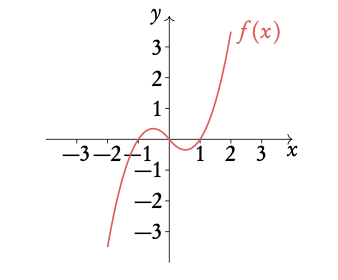
Transforming functions 2

2. Stretch the graph by the factor of a

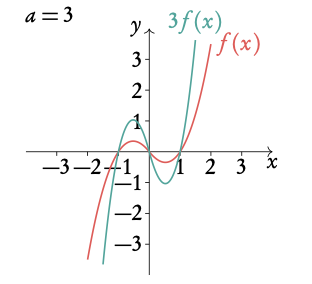
Transforming functions 3

3. Move graph by −b

Transforming functions 4

Frequently Asked Questions: Rearranging Functions & Solving for Variables

What does it mean to "rearrange a function" or equation?

Rearranging a function or equation means manipulating it algebraically to isolate a different variable on one side. Essentially, you are changing the "subject" of the formula. For example, if you have an equation solved for y (like y = 2x + 3), rearranging it might mean solving it for x instead.

Why is rearranging functions a useful skill?

Rearranging equations is fundamental in mathematics and many fields. It's useful for:

  • Solving for a specific variable in an equation.
  • Finding the inverse of a function.
  • Converting an equation into a standard form for graphing or analysis (like y = mx + b).
  • Solving problems where you are given the output but need to find the input.

What are the general steps for rearranging an equation?

The core principle is to use inverse operations to isolate the variable you want on one side of the equals sign. Remember to apply operations to *both sides* of the equation to maintain equality.

  1. Identify the variable you want to isolate.
  2. Undo any addition or subtraction terms attached to that variable's side by adding or subtracting the same value on both sides.
  3. Undo any multiplication or division terms by multiplying or dividing both sides by the same value.
  4. Undo any powers (like x²) by taking the corresponding root (square root).
  5. Undo any roots (like √x) by raising both sides to the corresponding power.
  6. Undo logarithmic functions by exponentiating both sides (using the base of the log).
  7. Undo exponential functions by taking the logarithm of both sides (using the base of the exponent).
  8. Undo trigonometric functions by using inverse trigonometric functions (like arcsin, arccos, arctan).
  9. Continue applying inverse operations until the desired variable is by itself on one side.

How do I rearrange equations with exponents?

To rearrange an equation where the variable is in the base of an exponent (e.g., y = x² or A = πr²), you use roots. If you need to solve for x in y = x², you take the square root of both sides: √y = √(x²), which gives x = ±√y (remembering the plus/minus for even powers).

If the variable is in the exponent (e.g., y = aˣ or P = P₀eᵏᵗ), you use logarithms. To solve for x in y = aˣ, you take the logarithm (often the natural log, ln) of both sides: ln(y) = ln(aˣ). Using log properties, this becomes ln(y) = x * ln(a). Then, divide by ln(a): x = ln(y) / ln(a).

How do I rearrange equations with logarithms or natural logs?

To rearrange an equation involving a logarithm (like y = logb(x) or y = ln(x)), you use the definition of logarithms or exponentiation. The definition logb(x) = y is equivalent to bʸ = x.

If your equation is y = logb(x) and you want to solve for x, you exponentiate both sides using the base b: bʸ = b^(logb(x)), which simplifies to x = bʸ.

For a natural log (base e), y = ln(x) is equivalent to eʸ = x. To solve for x, exponentiate both sides with base e: eʸ = e^(ln(x)), which simplifies to x = eʸ.

How do I rearrange equations with trigonometric functions?

To rearrange an equation where the variable is inside a trigonometric function (like y = sin(x) or A = cos(θ)), you use inverse trigonometric functions (arcsin, arccos, arctan, etc.).

If you have y = sin(x) and want to solve for x, you apply the inverse sine function (arcsin or sin⁻¹) to both sides: arcsin(y) = arcsin(sin(x)). This gives x = arcsin(y). Note that inverse trig functions often have restricted ranges, so this gives a principal value; there may be other solutions depending on the context.

How do I rearrange a linear equation into the form y = mx + b?

This form (slope-intercept form) requires isolating y on one side of the equation. Starting with a linear equation like Ax + By = C:

  1. Subtract the Ax term from both sides: By = C - Ax.
  2. Divide both sides by the coefficient of y (which is B): y = (C - Ax) / B.
  3. Separate the terms on the right side and rearrange: y = C/B - (A/B)x.
  4. Rewrite in y = mx + b form: y = (-A/B)x + C/B. Here, m = -A/B is the slope and b = C/B is the y-intercept.

Can software like Wolfram Mathematica rearrange functions?

Yes, computational software like Wolfram Mathematica, Symbolab, and even many graphing calculators have built-in functions or commands (often called Solve, Reduce, or InverseFunction) that can perform algebraic manipulations and rearrange equations to solve for specific variables.

Next Topic