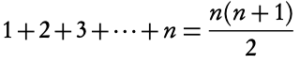Unlike direct proofs, where the result follows as a logical step, mathematical induction is a form of indirect proof (the only one covered in the IB syllabus). Indirect proofs tend to require a ‘creative’ step, however through training one can recognise most forms of induction.
Proof by induction can always be split up into three components, that together prove the wanted statement:

Common types: f(n) > g(n), f(n) = g(n), f(n) < g(n), Σ, P(n) is a multiple / divisible.
- Write statement in mathematical form
- Assume true for n = k
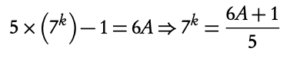
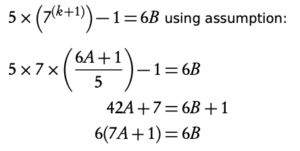
Hence, since P (1) true and assuming P(k) true, we have shown by the principle of mathematical induction that P(k + 1) true. Therefore, 5 × (7n) − 1 is divisible by 6 for all positive integers.
Induction
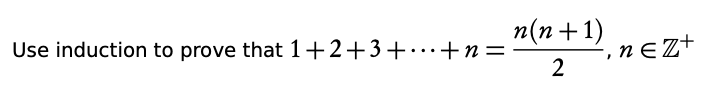
- Check for n = 1
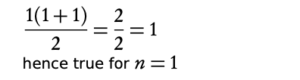
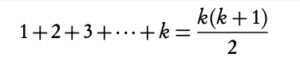

4. Write concluding statement
Hence, since n = 1 is true and assuming n = k true, we have shown by the principle of mathematical induction that n = k + 1 true. Therefore,