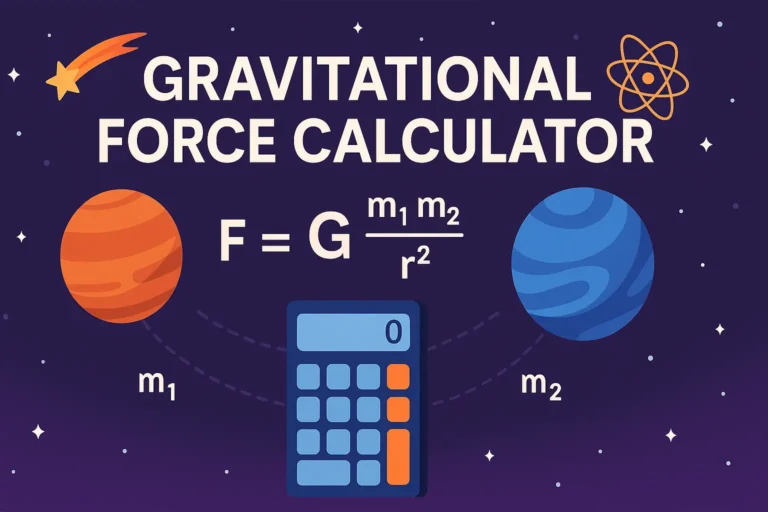
Gravitational Force Calculator - Newton's Law of Universal Gravitation
A gravitational force calculator is a physics tool that computes gravitational attraction between two masses using Newton's Law of Universal Gravitation, calculates acceleration due to gravity for planets and celestial bodies, and determines gravitational field strength at various distances from massive objects. Gravity is the fundamental force of attraction that exists between all objects with mass in the universe, governing planetary orbits, tides, satellite motion, and the structure of galaxies. Understanding gravitational calculations is essential in physics, astronomy, aerospace engineering, planetary science, and astrophysics where accurate gravity predictions affect spacecraft trajectories, satellite positioning, weight calculations, and orbital mechanics.
Newton's Law of Universal Gravitation states that every particle of matter in the universe attracts every other particle with a force proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The mathematical expression is \(F = G\frac{m_1 m_2}{r^2}\), where F is the gravitational force in Newtons, G is the universal gravitational constant (\(6.674 \times 10^{-11}\) N·m²/kg²), \(m_1\) and \(m_2\) are the masses of the two objects in kilograms, and r is the distance between their centers in meters. For surface gravity calculations, acceleration due to gravity follows \(g = \frac{GM}{r^2}\), where M is the planet's mass and r is its radius, yielding approximately 9.81 m/s² on Earth's surface.
Our comprehensive gravitational force calculator offers six specialized calculation modes to address diverse physics and astronomy applications. You can calculate gravitational force between two objects using Newton's universal law, determine acceleration due to gravity on planetary surfaces given mass and radius, compute gravitational field strength at any distance from a massive object, calculate the gravity of planets and moons in our solar system, determine orbital velocity and escape velocity using gravitational parameters, and analyze weight variations due to gravitational differences between celestial bodies. Each calculation mode provides detailed step-by-step solutions showing formulas, scientific notation handling, unit conversions, and intermediate calculations, making this tool invaluable for physics students, astronomy enthusiasts, aerospace engineers, astrophysicists, and anyone studying gravitational phenomena in celestial mechanics or planetary science.
Interactive Gravitational Force Calculator
Calculate Gravitational Force Between Two Objects
Calculate Acceleration Due to Gravity (g)
Calculate Gravitational Field Strength
Calculate Gravity of Planets
Calculate Orbital and Escape Velocity
Compare Weight on Different Planets
Essential Gravitational Formulas
Newton's Law of Universal Gravitation
Every particle attracts every other particle with a force proportional to the product of their masses and inversely proportional to the square of the distance between them.
Where F is gravitational force (N), G = 6.674 × 10⁻¹¹ N·m²/kg² (universal gravitational constant), m₁ and m₂ are masses (kg), and r is distance between centers (m).
Acceleration Due to Gravity
The acceleration experienced by objects near a massive body's surface, independent of the falling object's mass.
Where g is acceleration due to gravity (m/s²), G is gravitational constant, M is planet/body mass (kg), and r is radius from center (m). Earth's surface: g ≈ 9.81 m/s².
Gravitational Field Strength
The gravitational field strength at a point is the force per unit mass experienced by a small test mass at that point.
Gravitational field strength and acceleration due to gravity have the same formula and units (N/kg or m/s²). They represent the same physical quantity from different perspectives.
Weight Formula
Weight is the gravitational force acting on an object's mass. It varies with gravitational field strength.
Where W is weight (N), m is mass (kg), and g is local gravitational acceleration (m/s²). Weight changes with location; mass remains constant.
Orbital Velocity
The velocity required for an object to orbit a massive body at a given radius.
Where v is orbital velocity (m/s), M is central body mass (kg), and r is orbital radius (m). Lower orbits require higher velocities.
Escape Velocity
The minimum velocity needed for an object to escape a body's gravitational influence completely.
Where v_escape is escape velocity (m/s). Note: v_escape = √2 × v_orbital. Earth's surface escape velocity ≈ 11.2 km/s.
Planetary Gravity Reference Table
| Celestial Body | Mass (kg) | Radius (km) | Surface Gravity (m/s²) | Relative to Earth |
|---|---|---|---|---|
| Mercury | 3.30 × 10²³ | 2,439 | 3.70 | 0.38g |
| Venus | 4.87 × 10²⁴ | 6,052 | 8.87 | 0.90g |
| Earth | 5.97 × 10²⁴ | 6,371 | 9.81 | 1.00g |
| Moon | 7.35 × 10²² | 1,737 | 1.62 | 0.17g |
| Mars | 6.42 × 10²³ | 3,390 | 3.71 | 0.38g |
| Jupiter | 1.90 × 10²⁷ | 69,911 | 24.79 | 2.53g |
| Saturn | 5.68 × 10²⁶ | 58,232 | 10.44 | 1.07g |
| Uranus | 8.68 × 10²⁵ | 25,362 | 8.87 | 0.90g |
| Neptune | 1.02 × 10²⁶ | 24,622 | 11.15 | 1.14g |
| Sun | 1.99 × 10³⁰ | 696,000 | 274.0 | 27.9g |
Gravitational Constants and Values
| Constant/Value | Symbol | Value | Units |
|---|---|---|---|
| Universal Gravitational Constant | G | 6.674 × 10⁻¹¹ | N·m²/kg² or m³/(kg·s²) |
| Earth's Surface Gravity | g | 9.81 | m/s² or N/kg |
| Earth's Mass | M⊕ | 5.972 × 10²⁴ | kg |
| Earth's Radius (mean) | R⊕ | 6,371 | km |
| Solar Mass | M☉ | 1.989 × 10³⁰ | kg |
| Astronomical Unit | AU | 1.496 × 10¹¹ | m (≈ 150 million km) |
| Earth's Escape Velocity | v_e | 11.2 | km/s |
| Standard Acceleration of Gravity | g₀ | 9.80665 | m/s² (defined value) |
Key Takeaways
- Newton's Law: F = Gm₁m₂/r² - force proportional to masses, inversely proportional to distance squared
- Universal gravitational constant G = 6.674 × 10⁻¹¹ N·m²/kg²
- Acceleration due to gravity: g = GM/r² (independent of falling object's mass)
- Earth's surface gravity: g ≈ 9.81 m/s² (varies slightly by location)
- Weight W = mg (varies with location); mass remains constant everywhere
- Gravitational field strength and acceleration due to gravity are equivalent (N/kg = m/s²)
- Orbital velocity: v = √(GM/r) - higher velocity needed for lower orbits
- Escape velocity: v_e = √(2GM/r) = √2 × v_orbital
- Gravitational force is always attractive (never repulsive) and acts along line connecting centers
- Inverse square law: doubling distance reduces force to 1/4; tripling reduces to 1/9