3.1.1 Points in 3D space
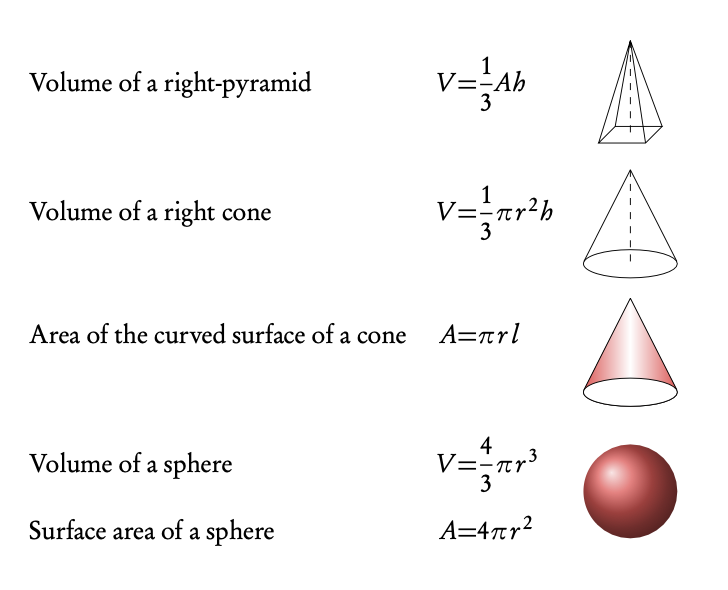
When you are learning about the points on a 2-dimensional plane, you also learn how to find distances between those two points. One of the easiest ways to derive that formula is by constructing a triangle and using Pythagoras. In the same way it is possible to derive a very similar expression for distance between two points in a 3D space:
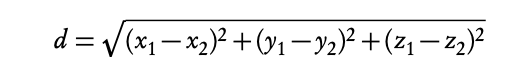
You have also learnt how to find the midpoint between the two points (x1,y1) and
(x2, y2): add those individual coordinates together and divide the sum by two. One can find the midpoint between two points in 3D space in almost exact same way:
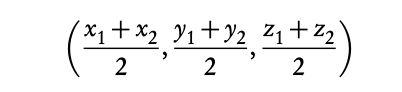
3.1.2 Pyramids, cones and spheres
In the exam you might be asked to find volume or surface of different 3D objects. These objects might be either familiar to you 3D shapes or made up from those shapes. In the first case, the formulas should be given in the data booklet. In the latter case, you would need to split the object into familiar shapes and sum the required components together.
DB 3.1