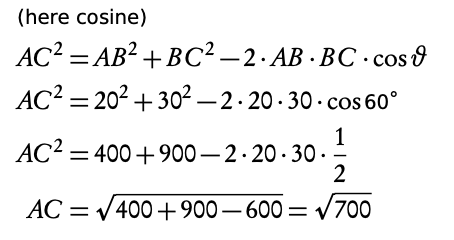This section offers an overview of some basic trigonometry rules and values that will recur often. It is worthwhile to know these by heart; but it is much better to understand how to obtain these values. Like converting between Celsius and Fahrenheit; you can remember some values that correspond to each other but if you understand how to obtain them, you will be able to convert any temperature.
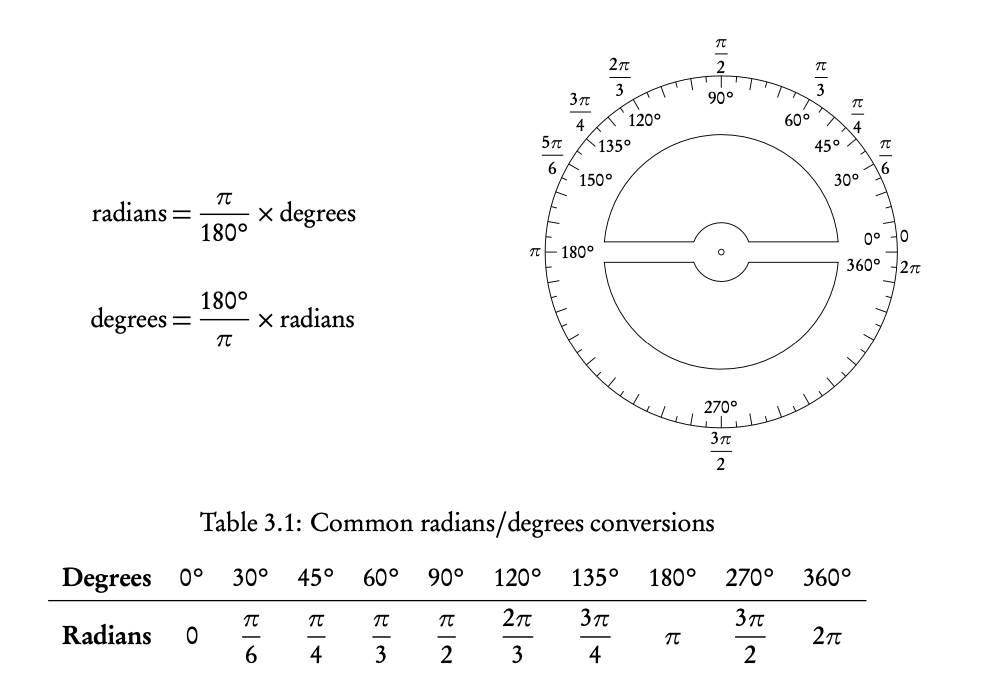
3.2.1 Converting between radians and degrees
3.2.2 Circle formulas
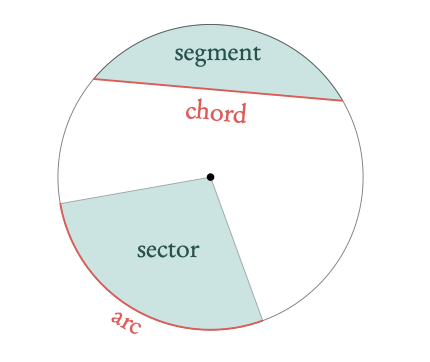
Area of a sector = ½ r2 · θ
Arc length = r · θ
θ in radians, r = radius.
DB. 3.4
3.2.3 Right-angle triangles
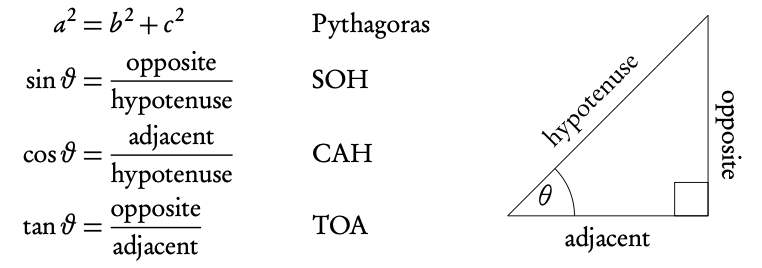
The following two right angle triangles with whole numbers for all the sides come up often in past exam questions.
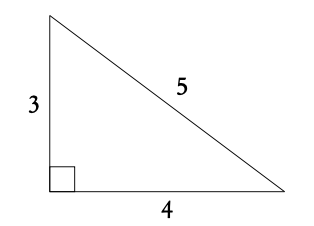
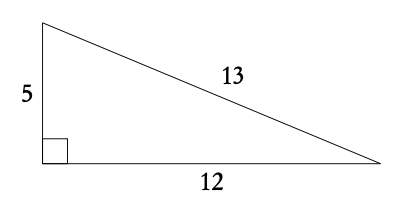
The two triangles below can help you in finding the sin, cos and tan of the angles that you should memorize, shown in table 3.2 on page 40. Use SOH, CAH, TOA to find the values.
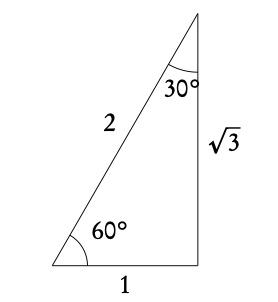
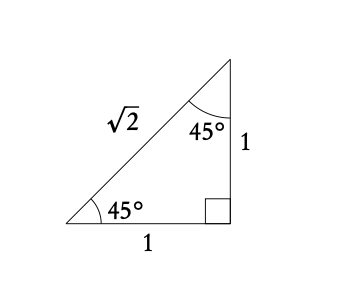
3.2.4 Non-right angle triangles
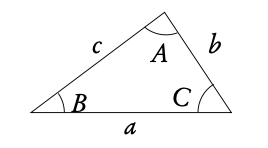
To find any missing angles or side lengths in non-right angle triangles, use the cosine and sine rule. Remember that the angles in the triangle add up to 180°!
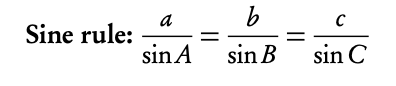
Use this rule when you know:
2 angles and a side
(not between the angles)
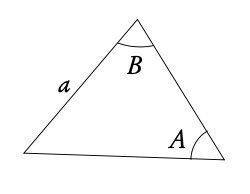
or
2 sides and an angle
(not between the sides)
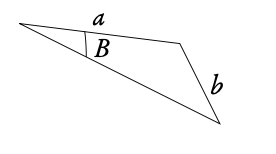
Cosine rule: c2 =a2 + b2 − 2ab cosC
Use this rule when you know:
3 sides
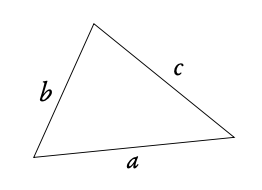
or
2 sides and the angle between them
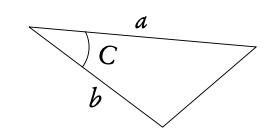
Area of a triangle: Area = ½ ab sinC
Use this rule when you know:
2 sides and the angle between them
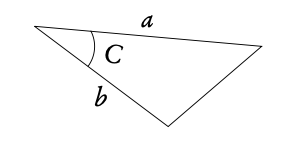
DB 3.2
Read the question: does it specify if you are looking for an acute (less than 90°) or obtuse (more than 90°) angle? If not there may be 2 solutions. Exam hint: Use sketches when working with worded questions!
Example: △ABC: A = 40°, B = 73°, a = 27 cm.

Example:
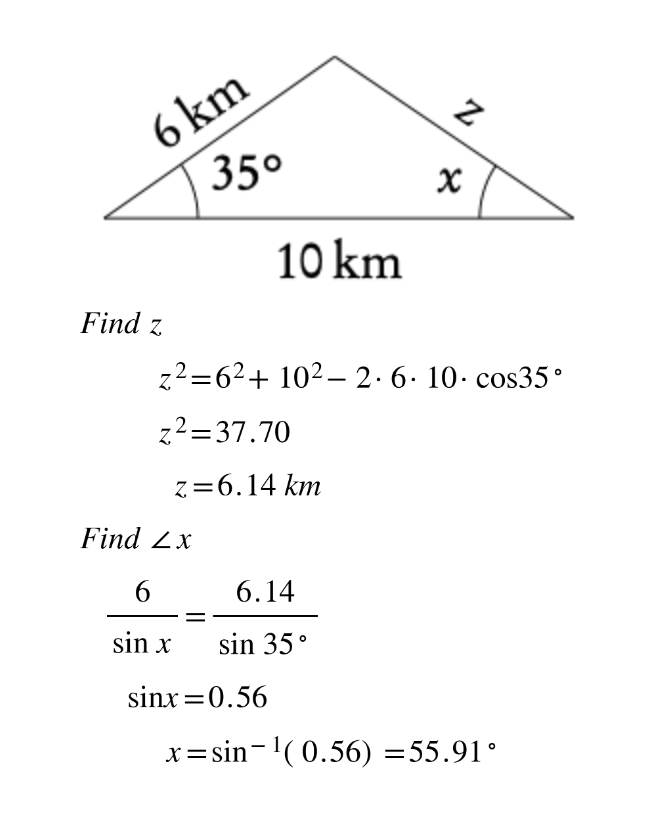
3.2.5 Ambiguous case
Ambiguous case, also known as an angle-side-side case, is when the triangle is not unique from the given information. It happens when you are given two sides and an angle not between those sides in a triangle.
You have to use a sine rule to solve a problem in this case. However, one needs to remember that sin x = sin(180° − x ), meaning that your answer for an angle is not just x , but also 180° − x.
In other words, we might get two different possible angles as an answer and thus two different possible triangles that satisfy the information given.
However, that is not always the case, if the sum of the two known angles becomes bigger than 180°. So if you are required to calculate the third angle or total area of a triangle, you might have to do the calculations for two different triangles using both of your angles.
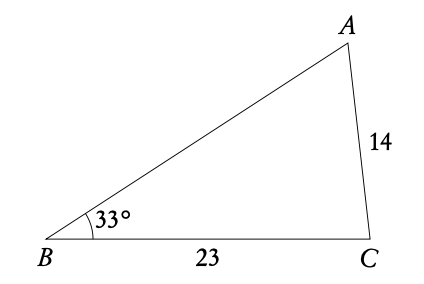
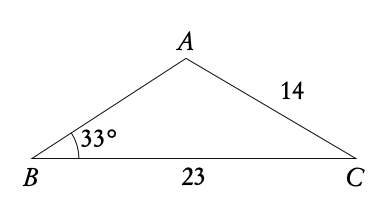
Example: △ABC : B = 33°, a = 23cm, b = 14cm. Find ∠A.
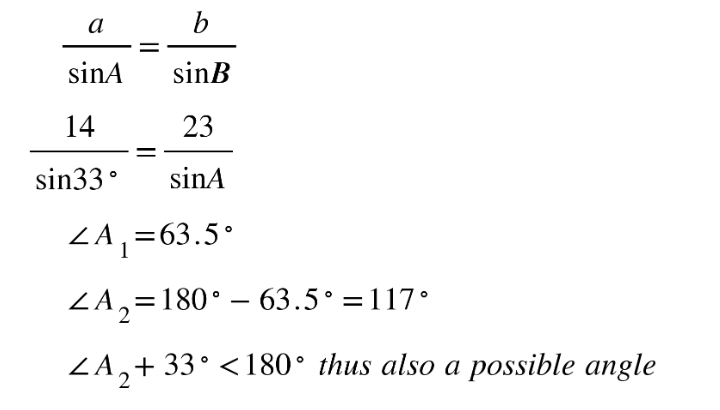
Draw the two possible triangles.
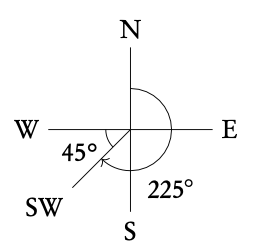
3.2.6 Three-figure bearings
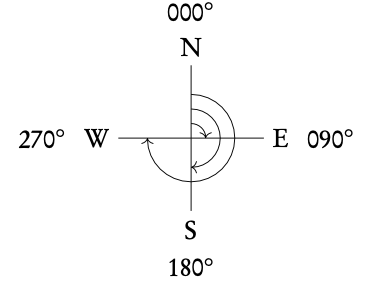
Three-figure bearings can be used to indicate compass directions on maps. They will be given as an angle of a full circle, so between 0° and 360°. North is always marked as 0°. Any direction from there can be expressed as the angle in the clockwise direction from North.
In questions on three-figure bearings, you are often confronted with quite a lot of text, so it is a good idea to first make a drawing. You may also need to create a right angle triangle and use your basic trigonometry.
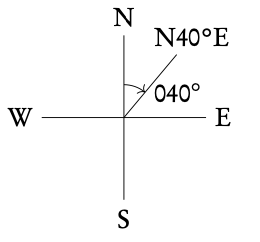
Example:
N40°E: 40° East of North = 40°
Solving questions with three-figure bearings
A ship left port A and sailed 20 km in the direction 120°. It then sailed north for 30 km to reach point C . How far from the port is the ship?
Sketch
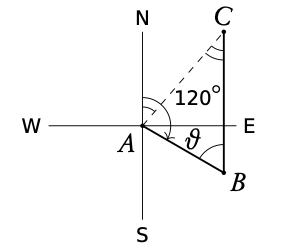
2. Find an internal angle of the triangle
θ = 180° − 120° = 60° = C
Similar angles between two parallel lines
3. Use cosine or sin rule