Frequency the number of times an event occurs in an experiment
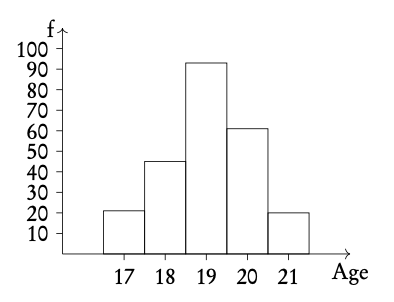
Cumulative frequency the sum of the frequency for a particular class and the frequencies for all the classes below it
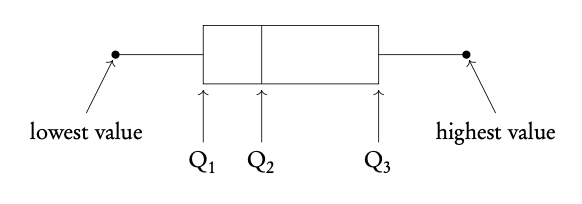
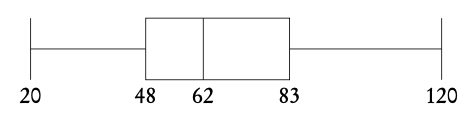
Box and whisker plots neatly summarize the distribution of the data. It gives information about the range, the median and the quartiles of the data. The first and third quartiles are at the ends of the box, the median is indicated with a vertical line in the interior of the box, and the maximum and minimum points are at the ends of the whiskers.
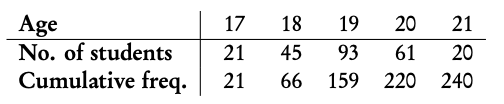
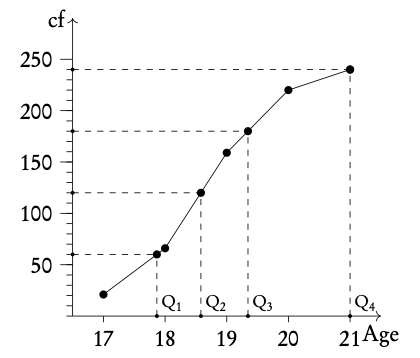
Example: Using the histogram, create a cumulative frequency graph and use it to construct a box and whisker diagram.
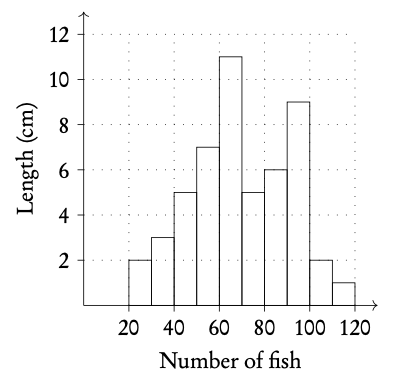
Write out the table for frequency and cumulative frequency.

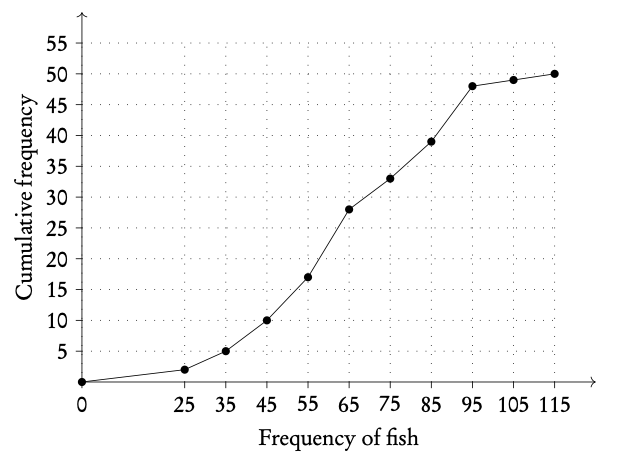
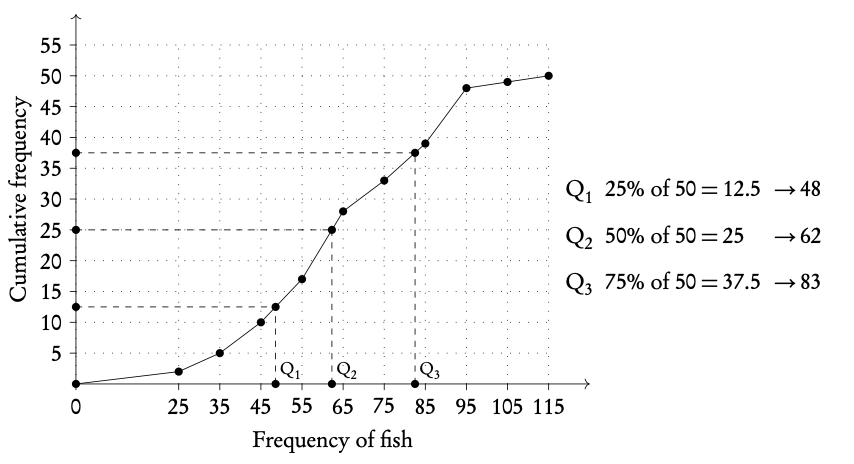
Plot box and whiskers.
GDC
Find the descriptive statistics for the data used in the previous example, showing the ages of students.


